Swing control for a three-link brachiation robot based on sliding-mode control on irregularly distributed bars

The bionic-gibbon robot is a popular bionic robot. The bionic-gibbon robot can imitate a gibbon in completing brachiation motion between branches. With nonlinear and underactuated properties, the robot has important research value. This paper designs a type of bionic-gibbon robot with three links and two grippers. To simplify the controller, a plane control model is proposed, and its dynamic model is established. The control strategy in this paper divides the brachiation motion into several processes: adjust posture, open the gripper, the swing process and close the gripper. Based on sliding-mode control (SMC), the control method for the swing process is designed. The target position of the brachiation motion is set as the origin of the sliding-mode surface. In a finite time, the robot will reach the target position along the approach rate we adopt. In this way, the robot can complete the desired brachiation motion only by setting the position parameters of the target bar. We perform some simulations in ROS-Gazebo. The simulation results show that the bionic-gibbon robot can complete continuous brachiation motion on irregularly distributed bars. The sliding-mode control and the three-link structure significantly improve the robustness and swing efficiency of the bionic-gibbon robot.

1 Introduction

Inspired by animals, many bionic robots have been designed and constructed. Inspired by the gibbon, as shown in Fig. 1 (Tashakori et al., 2020), a new bionic robot – the brachiation robot – has been designed. It moves forward by alternately swinging its body and grasping a bar like a gibbon. With nonlinear and underactuated characteristics, the brachiation robot has important research value.

Figure 1 The brachiation motion of the gibbon.

Saito et al. (1993) carried out earlier research on the brachiation robot, proposed a heuristic learning method for it and achieved the swing motion of the two-link brachiation robot. Hasegawa et al. (1999) introduced the self-scaling reinforcement learning algorithm to the brachiation robot controller, which improved the accuracy in grasping the bar. However, the two control methods require long training for the new bar at different positions. Nakanishi et al. (1997, 1998) proposed an alternative control method – target dynamics – for the brachiation robot. This method makes the robot swing like a pendulum. Therefore, starting from the posture of grabbing the single bar, the brachiation robot needs to swing several times to get energy before completing the first grab. It affects motion efficiency. Kajima et al. (2003, 2005, 2006) and Fukuda et al. (2006) achieved brachiation motion on a multi-locomotion robot – “Gorilla Robot III”. An energy-based control method was proposed and introduced into the swing motion controller. However, the robot could only perform continuous brachiation motion between the evenly distributed bars. Doi et al. (2006) applied the passive dynamic autonomous control method to the robot, which realized continuous swing on the irregular horizontal ladder. However, this irregularity was limited to the horizontal direction, and the vertical direction was not considered. Meghdari et al. (2013) presented a control method based on minimum control effort trajectory planning and tracking, and the CEDRA brachiation robot achieved brachiation motion on completely irregularly distributed bars. However, there was no research on the continuous swing. Nguyen and Liu (2017, 2019) developed two robust brachiation controllers and enabled the robot to swing along a structural member with an upward slope. However, the distribution of support rods was regular and lacked arbitrariness. The brachiation robot only considered the swing motion, not the grasping action. Wu et al. (2018) proposed big damping turn-back angle feedback and an energy pumping control strategy for the brachiation robot. This control strategy contained two control methods and divided the brachiation motion into four phases, which complicated the controller. In addition, the papers by Zhang et al. (2021), Hengmin et al. (2020) and Wang et al. (2020) also do relevant work.

Although a lot of research has been done on the brachiation robot, there are still some problems, such as grasping the target bars at different heights and distances, continuous brachiation and simplification of the controller. Meanwhile, most brachiation robots adopt the two-link model and ignore the body of the gibbon. In this paper, we design a three-link brachiation robot with two grippers. The robot achieves continuous brachiation motion on irregularly distributed bars. The irregular distribution of the bars can be at different distances and heights. Meanwhile, the controller is simple and robust.

The paper is organized as follows. In Sect. 2, the brachiation robot is presented. The plane control model is established based on the robot, and its dynamic model is introduced. In Sect. 3, we propose a control strategy for the robot, which divides the brachiation motion into four processes. Based on the sliding-mode control, we design a control method for the swing process of the robot. In Sect. 4, the simulation environment is established in ROS-Gazebo. The robot carries out single and continuous swing motion simulation. Finally, we analyse the simulation results.

2 The brachiation robot and control model

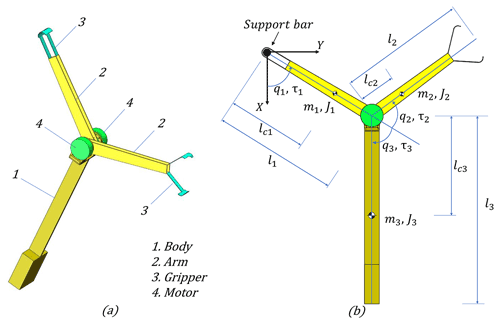
In this paper, a three-link brachiation robot is designed as shown in Fig. 2a. This robot has two arms and one body. Each arm has a gripper that can grasp a bar. Each arm is driven by a motor between the body and the arm. When a gripper grasps the bar, the gripper and the bar form a rotary joint that is assumed to be a passive joint. Therefore, the robot is an underactuated mechanism in the swing process. To simplify the controller, the robot is simplified to a plane model. Moreover, the plane model is idealized without friction and disturbance, and the grippers in the closed state are considered to be part of the arm. We establish a plane control model for the controller as shown in Fig. 2b. Where m_i, l_i and l_ci are the mass, length and centre of mass of link i, $\left(i=\mathrm{1},\mathrm{2},\mathrm{3}\right)$, respectively. J_i is the moment of inertia of link i about the rotation axis. Respectively, q_i and τ_i are generalized angle and generalized torque. The kinematic and dynamic parameter values of the brachiation robot control model are shown in Table 1. There τ_ei represents the maximum torque of the motor.

Figure 2 (a) The brachiation robot. (b) The plane control model of the brachiation robot.

Table 1 The parameters of the control model.

By the Lagrange equation, the dynamic equation of the system is as follows:

$$\begin{array}{}\text{(1)}& \mathbf{M}\left(\mathit{q}\right)\ddot{\mathit{q}}+\mathbf{H}\left(\mathit{q},\dot{\mathit{q}}\right)=\mathit{\tau },\end{array}$$

where $\mathit{q}={\left[q_{\mathrm{1}}{q}_{\mathrm{2}}{q}_{\mathrm{3}}\right]}^{\mathrm{T}}$, $\mathit{\tau }={\left[{\mathit{\tau }}_{\mathrm{1}}{\mathit{\tau }}_{\mathrm{2}}{\mathit{\tau }}_{\mathrm{3}}\right]}^{\mathrm{T}}$, τ₁=0, M(q) is the inertial matrix, and it is reversible, The corresponding proof is in Murray et al. (1994). Because the inertia matrix M(q) is symmetric and positive definite, according to the knowledge of linear algebra, we can find that the inertia matrix M(q) is invertible. $\mathbf{H}\left(\mathit{q},\dot{\mathit{q}}\right)$ represents the nonlinear Coriolis, centrifugal force, and gravity term. The matrix M(q) and vector $\mathbf{H}\left(\mathit{q},\dot{\mathit{q}}\right)$ are given by

$$\mathbf{M}\left(\mathit{q}\right)=\left[\begin{array}{ccc}{m}_{\mathrm{11}}& m_{\mathrm{12}}& m_{\mathrm{13}}\\ m_{\mathrm{21}}& m_{\mathrm{22}}& m_{\mathrm{23}}\\ m_{\mathrm{31}}& m_{\mathrm{32}}& m_{\mathrm{33}}\end{array}\right],$$

where

$$\begin{array}{c}{\displaystyle }\begin{array}{rl}{m}_{\mathrm{11}}& =J_{\mathrm{1}}+m_{\mathrm{1}}{L}_{c\mathrm{1}}^{\mathrm{2}}+J_{\mathrm{2}}+m_{\mathrm{2}}{L}_{\mathrm{1}}^{\mathrm{2}}+m_{\mathrm{2}}{L}_{c\mathrm{2}}^{\mathrm{2}}\\ & +\mathrm{2}{m}_{\mathrm{2}}{L}_{\mathrm{1}}{L}_{c\mathrm{2}}\cos \left(q_{\mathrm{2}}\right)+J_{\mathrm{3}}+m_{\mathrm{3}}{L}_{\mathrm{1}}^{\mathrm{2}}+m_{\mathrm{3}}{L}_{c\mathrm{3}}^{\mathrm{2}}\\ & +\mathrm{2}{m}_{\mathrm{3}}{L}_{\mathrm{1}}{L}_{c\mathrm{3}}\cos \left(q_{\mathrm{3}}\right),\end{array}\\ {\displaystyle }{m}_{\mathrm{12}}=J_{\mathrm{2}}+m_{\mathrm{2}}{L}_{c\mathrm{2}}^{\mathrm{2}}+m_{\mathrm{2}}{L}_{\mathrm{1}}{L}_{c\mathrm{2}}\cos \left(q_{\mathrm{2}}\right),\\ {\displaystyle }{m}_{\mathrm{13}}=J_{\mathrm{3}}+m_{\mathrm{3}}{L}_{c\mathrm{3}}^{\mathrm{2}}+m_{\mathrm{3}}{L}_{\mathrm{1}}{L}_{c\mathrm{3}}\cos \left(q_{\mathrm{3}}\right),\\ {\displaystyle }{m}_{\mathrm{21}}=J_{\mathrm{2}}+m_{\mathrm{2}}{L}_{c\mathrm{2}}^{\mathrm{2}}+m_{\mathrm{2}}{L}_{\mathrm{1}}{L}_{c\mathrm{2}}\cos \left(q_{\mathrm{2}}\right),\\ {\displaystyle }{m}_{\mathrm{22}}=J_{\mathrm{2}}+m_{\mathrm{2}}{L}_{c\mathrm{2}}^{\mathrm{2}},\\ {\displaystyle }{m}_{\mathrm{23}}=\mathrm{0},\\ {\displaystyle }{m}_{\mathrm{31}}=J_{\mathrm{3}}+m_{\mathrm{3}}{L}_{c\mathrm{3}}^{\mathrm{2}}+m_{\mathrm{3}}{L}_{\mathrm{1}}{L}_{c\mathrm{3}}\cos \left(q_{\mathrm{3}}\right),\\ {\displaystyle }{m}_{\mathrm{32}}=\mathrm{0},\\ {\displaystyle }{m}_{\mathrm{33}}=J_{\mathrm{3}}+m_{\mathrm{3}}{L}_{c\mathrm{3}}^{\mathrm{2}},\\ {\displaystyle }\mathbf{H}\left(\mathit{q},\dot{\mathit{q}}\right)=\left[\begin{array}{c}{h}_{\mathrm{1}}\\ h_{\mathrm{2}}\\ h_{\mathrm{3}}\end{array}\right],\end{array}$$

where

$$\begin{array}{c}{\displaystyle }\begin{array}{rl}{h}_{\mathrm{1}}& =-m_{\mathrm{2}}{L}_{\mathrm{1}}{L}_{c\mathrm{2}}\sin \left(q_{\mathrm{2}}\right)\left(\mathrm{2}{\dot{q}}_{\mathrm{1}}{\dot{q}}_{\mathrm{2}}+{\dot{q}}_{\mathrm{2}}^{\mathrm{2}}\right)\\ & -m_{\mathrm{3}}{L}_{\mathrm{1}}{L}_{c\mathrm{3}}\sin \left(q_{\mathrm{3}}\right)\left(\mathrm{2}{\dot{q}}_{\mathrm{1}}{\dot{q}}_{\mathrm{3}}+{\dot{q}}_{\mathrm{3}}^{\mathrm{2}}\right)\\ & +\left(m_{\mathrm{1}}{L}_{c\mathrm{1}}+m_{\mathrm{2}}{L}_{\mathrm{1}}+m_{\mathrm{3}}{L}_{\mathrm{1}}\right)g\cos \left(q_{\mathrm{1}}\right)\\ & +m_{\mathrm{2}}g{L}_{c\mathrm{2}}\cos \left(q_{\mathrm{1}}+q_{\mathrm{2}}\right)+m_{\mathrm{3}}g{L}_{c\mathrm{3}}\cos \left(q_{\mathrm{1}}+q_{\mathrm{3}}\right),\end{array}\\ {\displaystyle }{h}_{\mathrm{2}}=m_{\mathrm{2}}{L}_{\mathrm{1}}{L}_{c\mathrm{2}}\sin \left(q_{\mathrm{2}}\right){\dot{q}}_{\mathrm{1}}^{\mathrm{2}}+m_{\mathrm{2}}g{L}_{c\mathrm{2}}\cos \left(q_{\mathrm{1}}+q_{\mathrm{2}}\right),\\ {\displaystyle }{h}_{\mathrm{3}}=m_{\mathrm{3}}{L}_{\mathrm{1}}{L}_{c\mathrm{3}}\sin \left(q_{\mathrm{3}}\right){\dot{q}}_{\mathrm{1}}^{\mathrm{2}}+m_{\mathrm{3}}g{L}_{c\mathrm{3}}\cos \left(q_{\mathrm{1}}+q_{\mathrm{3}}\right).\end{array}$$

What needs to be emphasized is that τ₂ and τ₃ are generalized torque in the control model. We finally want to get the torque τ₄ of the motor between the body and the support arm and the torque τ₅ of the motor between the body and the swing arm. Through Newton's third law, we can get

$$\begin{array}{}\text{(2)}& \begin{array}{rl}& {\mathit{\tau }}_{\mathrm{4}}={\mathit{\tau }}_{\mathrm{2}}+{\mathit{\tau }}_{\mathrm{3}},\\ & {\mathit{\tau }}_{\mathrm{5}}={\mathit{\tau }}_{\mathrm{2}}.\end{array}\end{array}$$

3 Design of the controller

3.1 The control strategy of the brachiation motion

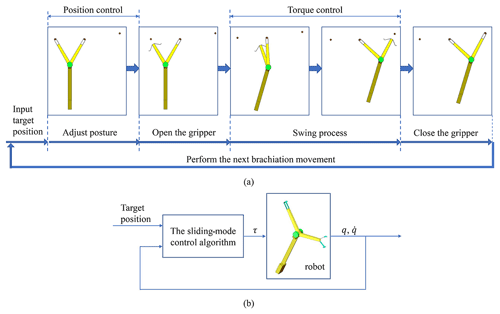
By analysing the brachiation motion of the gibbon, we project the brachiation motion of the robot as shown in Fig. 3a. The motion process is divided into four steps: (1) adjust posture, (2) open the gripper, (3) the swing process, and (4) close the gripper. In step (1), the controller is provided with the position of the target bar and adjusts the robot's posture. When the two grippers grasp the bars, the robot forms redundant constraints with the two bars. Therefore, in this step, precise position control is required to keep the robot in a certain posture to prepare for the next swing motion. In step (2), open a gripper by position control and start the swing process. In step (3), the robot swings from the initial position to the target position. In this step, the robot is underactuated. The controller adopts torque control to control the robot by using the sliding-mode control algorithm. According to the target position and robot state, the sliding-mode control algorithm as shown in Fig. 3b can get the control torque of the motor. In step (4), when the swing arm reaches the target point, the gripper closes and the robot completes a single brachiation motion. After that, the robot can perform the next single brachiation motion to achieve continuous brachiation motion.

Figure 3 (a) Motion flow for continuous brachiation. (b) The control flow of the swing process.

3.2 The sliding-mode control algorithm

The sliding-mode control (Utkin, 1977) is a type of nonlinear control method. It is easy to implement and has stronger robustness to disturbances (Young et al., 1999). Meanwhile, this control method with fast response is suitable for fast swing motion. Therefore, this paper selects the sliding-mode control and applies it to the brachiation motion. To introduce this control method into the robot controller, the target position of brachiation motion is set as the origin of the sliding-mode surface. Suppose that when the gripper reaches the target point, the values of q₁ and q₂ are q_d1 and q_d2. Select the sliding-mode surface function as follows:

$$\begin{array}{}\text{(3)}& \mathit{S}=\left[\begin{array}{c}{s}_{\mathrm{1}}\\ s_{\mathrm{2}}\end{array}\right]=\left[\begin{array}{c}{c}_{\mathrm{1}}\left(q_{\mathrm{1}}-q_{d\mathrm{1}}\right)+{\dot{q}}_{\mathrm{1}}\\ c_{\mathrm{2}}\left(q_{\mathrm{2}}-q_{d\mathrm{2}}\right)+{\dot{q}}_{\mathrm{2}}\end{array}\right];\end{array}$$

here, c₁ and c₂ are the control parameters. Then,

$$\begin{array}{}\text{(4)}& \dot{\mathit{S}}=\left[\begin{array}{c}{\dot{s}}_{\mathrm{1}}\\ {\dot{s}}_{\mathrm{2}}\end{array}\right]=\left[\begin{array}{c}{c}_{\mathrm{1}}{\dot{q}}_{\mathrm{1}}+{\ddot{q}}_{\mathrm{1}}\\ c_{\mathrm{2}}{\dot{q}}_{\mathrm{2}}+{\ddot{q}}_{\mathrm{2}}\end{array}\right].\end{array}$$

Eq. (1) can be rewritten as follows:

$$\begin{array}{}\text{(5)}& \begin{array}{rl}& {\ddot{q}}_{\mathrm{1}}=n_{\mathrm{11}}\left(-h_{\mathrm{1}}\right)+n_{\mathrm{12}}\left({\mathit{\tau }}_{\mathrm{2}}-h_{\mathrm{2}}\right)+n_{\mathrm{13}}\left({\mathit{\tau }}_{\mathrm{3}}-h_{\mathrm{3}}\right),\\ & {\ddot{q}}_{\mathrm{2}}=n_{\mathrm{21}}\left(-h_{\mathrm{1}}\right)+n_{\mathrm{22}}\left({\mathit{\tau }}_{\mathrm{2}}-h_{\mathrm{2}}\right)+n_{\mathrm{23}}\left({\mathit{\tau }}_{\mathrm{3}}-h_{\mathrm{3}}\right),\end{array}\end{array}$$

where n₁₁, n₁₂, n₁₃, n₂₁, n₂₂ and n₂₃ are the elements of M(q)⁻¹. Substituting ${\ddot{q}}_{\mathrm{1}}$ and ${\ddot{q}}_{\mathrm{2}}$ from Eq. (5) into Eq. (4) yields

$$\begin{array}{}\text{(6)}& \dot{\mathit{S}}=\left[\begin{array}{c}{\dot{s}}_{\mathrm{1}}\\ {\dot{s}}_{\mathrm{2}}\end{array}\right]=\left[\begin{array}{l}{c}_{\mathrm{1}}{\dot{q}}_{\mathrm{1}}+n_{\mathrm{11}}\left(-h_{\mathrm{1}}\right)+n_{\mathrm{12}}\left({\mathit{\tau }}_{\mathrm{2}}-h_{\mathrm{2}}\right)\\ +n_{\mathrm{13}}\left({\mathit{\tau }}_{\mathrm{3}}-h_{\mathrm{3}}\right)\\ c_{\mathrm{2}}{\dot{q}}_{\mathrm{2}}+n_{\mathrm{21}}\left(-h_{\mathrm{1}}\right)+n_{\mathrm{22}}\left({\mathit{\tau }}_{\mathrm{2}}-h_{\mathrm{2}}\right)\\ +n_{\mathrm{23}}\left({\mathit{\tau }}_{\mathrm{3}}-h_{\mathrm{3}}\right)\end{array}\right].\end{array}$$

In the sliding-mode control algorithm, the new approach law, “fast power reaching law” in Yu et al. (2005), is adopted. Then,

$$\begin{array}{}\text{(7)}& \dot{\mathit{S}}=\left[\begin{array}{c}{\dot{s}}_{\mathrm{1}}\\ {\dot{s}}_{\mathrm{2}}\end{array}\right]=\left[\begin{array}{c}-k_{\mathrm{1}}{s}_{\mathrm{1}}-k_{\mathrm{2}}{\left|s_{\mathrm{1}}\right|}^{{\mathit{\alpha }}_{\mathrm{1}}}\mathrm{sgn}\left(s_{\mathrm{1}}\right)\\ -k_{\mathrm{3}}{s}_{\mathrm{2}}-k_{\mathrm{4}}{\left|s_{\mathrm{2}}\right|}^{{\mathit{\alpha }}_{\mathrm{2}}}\mathrm{sgn}\left(s_{\mathrm{2}}\right)\end{array}\right];\end{array}$$

here, k₁>0, k₂>0, k₃>0, k₄>0, $\mathrm{0}<{\mathit{\alpha }}_{\mathrm{1}}<\mathrm{1}$ and $\mathrm{0}<{\mathit{\alpha }}_{\mathrm{2}}<\mathrm{1}$. This approach rate can effectively suppress the oscillates about the sliding manifold. Through Eqs. (6) and (7) we can get the control torque as follows:

$$\begin{array}{}\text{(8)}& \begin{array}{rl}\left[\begin{array}{c}{\mathit{\tau }}_{\mathrm{2}}\\ {\mathit{\tau }}_{\mathrm{3}}\end{array}\right]& ={\left[\begin{array}{cc}{n}_{\mathrm{12}}& n_{\mathrm{13}}\\ n_{\mathrm{22}}& n_{\mathrm{23}}\end{array}\right]}^{-\mathrm{1}}\\ & \cdot \left[\begin{array}{l}-k_{\mathrm{1}}{s}_{\mathrm{1}}-k_{\mathrm{2}}{\left|s_{\mathrm{1}}\right|}^{{\mathit{\alpha }}_{\mathrm{1}}}\mathrm{sgn}\left(s_{\mathrm{1}}\right)-c_{\mathrm{1}}{\dot{q}}_{\mathrm{1}}\\ +n_{\mathrm{11}}{h}_{\mathrm{1}}+n_{\mathrm{12}}{h}_{\mathrm{2}}+n_{\mathrm{13}}{h}_{\mathrm{3}}\\ -k_{\mathrm{3}}{s}_{\mathrm{2}}-k_{\mathrm{4}}{\left|s_{\mathrm{2}}\right|}^{{\mathit{\alpha }}_{\mathrm{2}}}\mathrm{sgn}\left(s_{\mathrm{2}}\right)-c_{\mathrm{2}}{\dot{q}}_{\mathrm{2}}+n_{\mathrm{21}}{h}_{\mathrm{1}}\\ +n_{\mathrm{22}}{h}_{\mathrm{2}}+n_{\mathrm{23}}{h}_{\mathrm{3}}\end{array}\right].\end{array}\end{array}$$

In the next simulation, the validity of Eq. (8) will be guaranteed. Through Eq. (2), we can get the final control target τ₄ and τ₅.

Consider the following Lyapunov function candidate:

$$\begin{array}{}\text{(9)}& V={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}{\mathit{S}}^{\mathrm{T}}\mathit{S}.\end{array}$$

Then,

$$\begin{array}{}\text{(10)}& \begin{array}{rl}\dot{V}& =s_{\mathrm{1}}{\dot{s}}_{\mathrm{1}}+s_{\mathrm{2}}{\dot{s}}_{\mathrm{2}}\\ & =-k_{\mathrm{1}}{s}_{\mathrm{1}}^{\mathrm{2}}-k_{\mathrm{2}}{\left|s_{\mathrm{1}}\right|}^{{\mathit{\alpha }}_{\mathrm{1}}+\mathrm{1}}-k_{\mathrm{3}}{s}_{\mathrm{2}}^{\mathrm{2}}-k_{\mathrm{4}}{\left|s_{\mathrm{2}}\right|}^{{\mathit{\alpha }}_{\mathrm{2}}+\mathrm{1}}\le \mathrm{0}.\end{array}\end{array}$$

When the brachiation robot does not reach the target point, V>0 and $\dot{V}<\mathrm{0}$. According to the Lyapunov theorem for global stability, it can be deduced that the target point is globally asymptotically stable. Next, we will prove the convergence law of tracking error. According to Eq. (10) we can get

$$\begin{array}{}\text{(11)}& \dot{V}\le -\mathit{\alpha }V,\mathrm{0}<\mathit{\alpha }\le \mathrm{2}min\left\{k_{\mathrm{1}},k_{\mathrm{3}}\right\}.\end{array}$$

According to Lemma 3.2.4 in Ioannou and Sun (1995), we can get

$$\begin{array}{}\text{(12)}& V\left(t\right)\le e^{-\mathit{\alpha }\left(t-t_{\mathrm{0}}\right)}V\left(t_{\mathrm{0}}\right).\end{array}$$

So, V exponentially converges to zero, and the convergence rate depends on α.

4 Simulation and result analysis

To verify the efficiency of the robot brachiation controller we design, the brachiation robot is established in the simulation software Gazebo as shown in Fig. 2a, and we establish the control system by using ROS-Gazebo. ROS is a popular operating system in robot development, and Gazebo is physical simulation software compatible with ROS. The control parameters are set: c₁=10, c₂=10, k₁=100, k₂=0.5, k₃=1000, k₄=0.5, α₁=0.5 and α₂=0.5. Next, the simulation experiment of single and continuous brachiation motion is carried out.

4.1 The single brachiation movement

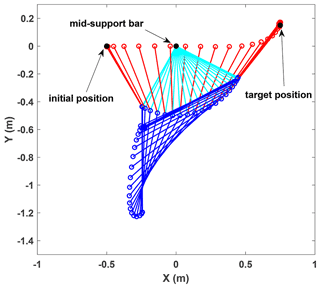
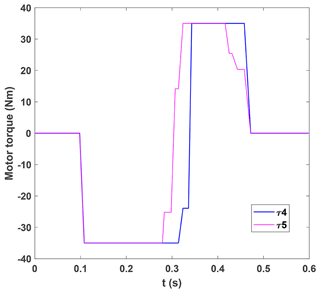
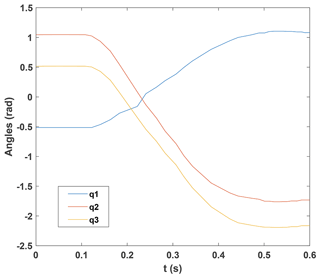
The single swing process of the brachiation robot is shown in Fig. 4. We select the initial position ($x=-\mathrm{0.5}$ m, y=0 m) and the target position (x=0.75 m, y=0.15 m). Compared with the distance between the initial position and the mid-support bar, the distance between the target position and the mid-support bar changes in the horizontal and vertical directions. This ensures the arbitrariness of the target point. Control torque is shown in Fig. 5. Due to the limitation of motor torque, the saturation constraint is applied to Eq. (2). The motor torque is limited to [−35, 35] N m. This reflects the robustness of the controller to the motor torque limitation. The angle value of the brachiation robot is shown in Fig. 6. We can see that the torque control starts to work at 0.08 s. It ends at 0.47 s and the torque of the motor returns to zero. The brachiation robot reaches the target bar only through the first swing, which improves the movement efficiency.

Besides, the controller is designed based on the plane control mode without considering joint friction and the action of the grippers in Eq. (1). However, it is used to control the three-dimensional brachiation robot with grippers and joint friction in Gazebo. Simulation results show that the controller has strong robustness for the robot with the uncertainties model and the action of the grippers.

Figure 4 The single swing process of the brachiation robot.

Figure 5 The motor torque of the brachiation robot.

Figure 6 The angles of the brachiation robot.

To evaluate the swing ability of different brachiation robots, we define two evaluation indexes: swing efficiency and swing height.

Definition 1: swing efficiency is the horizontal distance that the robot can reach with a single swing, divided by the length of the two arms.

Definition 2: swing height is the height that the robot can reach with a single swing.

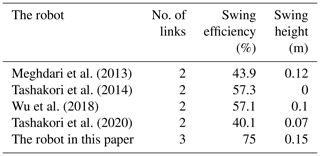
Through the two evaluation indexes, the three-link robot in this paper is compared with the two-link brachiation robots as shown in Table 2. We can see that the three-link structure improves the swing efficiency and swing height of the brachiation robot. The three-link robot has one more motor than the two-link robot. Therefore, the three-link robot has a stronger adjustment force. In addition, the third link adds mass and moment of inertia to the dynamic system of the robot, which enhances the balance ability of the system and increases the range of motion of the two arms.

Table 2 Swing ability of different robots.

4.2 The continuous brachiation movement

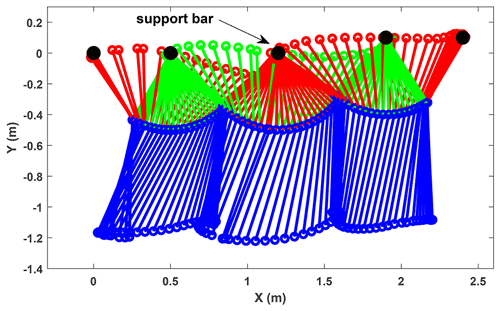
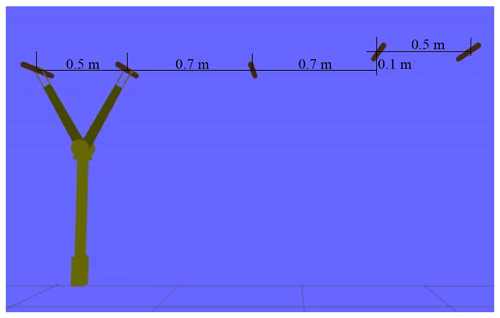
The continuous swing process of the brachiation robot on irregularly distributed bars is shown in Fig. 7. The positions of the five support bars are (x=0 m, y=0 m), (x=0.5 m, y=0 m), (x=1.2 m, y=0 m), (x=1.9 m, y=0.1 m) and (x=2.4 m, y=0.1 m). Compared with evenly distributed bars, the positions of the irregularly distributed bars have changed in the horizontal and vertical directions. In Fig. 7 we can observe the position and posture of the robot at different moments in the swing process. The robot continuously completes three single brachiation motions. The initial positions relative to the mid-support bar of each swing are ($x=-\mathrm{0.5}$ m, y=0 m), ($x=-\mathrm{0.7}$ m, y=0 m) and ($x=-\mathrm{0.7}$ m, $y=-\mathrm{0.1}$ m). The target positions relative to the mid-support bar of each swing are (x=0.7 m, y=0 m), (x=0.7 m, y=0.1 m) and (x=0.5 m, y=0 m). In each single swing motion, the initial positions and target positions have changed. The simulation results show that the controller is robust to different initial positions and target positions.

Figure 7 The continuous swing process of the brachiation robot.

Figure 8 The simulation environment in Gazebo.

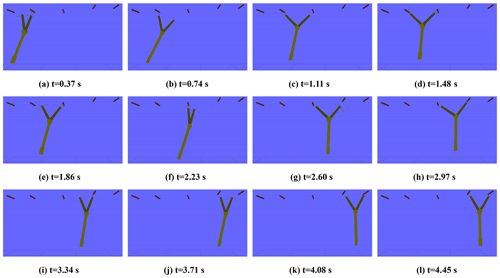
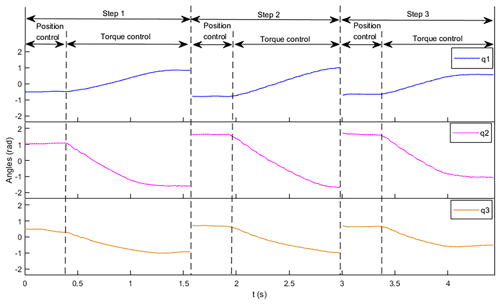
The simulation environment is set up in Gazebo as shown in Fig. 8, which shows the initial state of the brachiation robot and the distribution of support bars. The simulation of the continuous swing motion in Gazebo is shown in Fig. 9. The robot performs the first single swing motion in Fig. 9a–d, the second one in Fig. 9e–h and the third one in Fig. 9i–l. The angle value of the continuous swing is shown in Fig. 10. The robot completes the first single swing motion at 1.58 s, the second one at 2.94 s and the third one at 4.43 s. After every single swing, the roles of the swing arm and the support arm are swapped. Meanwhile, the angle value of the control model also changes, which is not continuous, as shown in Fig. 10. In the position control phase, the angle value is relatively stable. The robot can maintain a certain state, which provides a stable initial posture for the next swing process. In the torque control phase, the angle changes monotonously. The robot quickly reaches the target position.

Figure 9 The continuous swing process of the brachiation robot in Gazebo.

Figure 10 The angles of the brachiation robot.

4.3 Disturbance analysis

The swing motion of the brachiation robot is often influenced by various disturbances. To verify the effectiveness of the proposed control scheme under complex disturbances, a disturbance analysis is performed. The disturbance term is added to the control input, and Eq. (1) can be rewritten as follows:

$$\begin{array}{}\text{(13)}& \begin{array}{rl}& {\ddot{q}}_{\mathrm{1}}=n_{\mathrm{11}}\left(-h_{\mathrm{1}}\right)+n_{\mathrm{12}}\left({\mathit{\tau }}_{\mathrm{2}}-h_{\mathrm{2}}\right)+n_{\mathrm{13}}\left({\mathit{\tau }}_{\mathrm{3}}-h_{\mathrm{3}}\right)+d_{\mathrm{1}},\\ & {\ddot{q}}_{\mathrm{2}}=n_{\mathrm{21}}\left(-h_{\mathrm{1}}\right)+n_{\mathrm{22}}\left({\mathit{\tau }}_{\mathrm{2}}-h_{\mathrm{2}}\right)+n_{\mathrm{23}}\left({\mathit{\tau }}_{\mathrm{3}}-h_{\mathrm{3}}\right)+d_{\mathrm{2}},\end{array}\end{array}$$

where, supposing that $d_{\mathrm{1}}=A\cos \left(\frac{\mathrm{2}\mathit{\pi }}{T}t\right)$ and $d_{\mathrm{2}}=A\sin \left(\frac{\mathrm{2}\mathit{\pi }}{T}t\right)$, A is the amplitude and T is the period. Substituting ${\ddot{q}}_{\mathrm{1}}$ and ${\ddot{q}}_{\mathrm{2}}$ from Eq. (13) into Eq. (4) yields

$$\begin{array}{}\text{(14)}& \dot{\mathit{S}}=\left[\begin{array}{c}{\dot{s}}_{\mathrm{1}}\\ {\dot{s}}_{\mathrm{2}}\end{array}\right]=\left[\begin{array}{l}{c}_{\mathrm{1}}{\dot{q}}_{\mathrm{1}}+n_{\mathrm{11}}\left(-h_{\mathrm{1}}\right)+n_{\mathrm{12}}\left({\mathit{\tau }}_{\mathrm{2}}-h_{\mathrm{2}}\right)\\ +n_{\mathrm{13}}\left({\mathit{\tau }}_{\mathrm{3}}-h_{\mathrm{3}}\right)+d_{\mathrm{1}}\\ c_{\mathrm{2}}{\dot{q}}_{\mathrm{2}}+n_{\mathrm{21}}\left(-h_{\mathrm{1}}\right)+n_{\mathrm{22}}\left({\mathit{\tau }}_{\mathrm{2}}-h_{\mathrm{2}}\right)\\ +n_{\mathrm{23}}\left({\mathit{\tau }}_{\mathrm{3}}-h_{\mathrm{3}}\right)+d_{\mathrm{2}}\end{array}\right].\end{array}$$

Through Eqs. (14) and (7) we can get the control torque as follows:

$$\begin{array}{}\text{(15)}& \begin{array}{rl}\left[\begin{array}{c}{\mathit{\tau }}_{\mathrm{2}}\\ {\mathit{\tau }}_{\mathrm{3}}\end{array}\right]& ={\left[\begin{array}{cc}{n}_{\mathrm{12}}& n_{\mathrm{13}}\\ n_{\mathrm{22}}& n_{\mathrm{23}}\end{array}\right]}^{-\mathrm{1}}\\ & \cdot \left[\begin{array}{l}-k_{\mathrm{1}}{s}_{\mathrm{1}}-k_{\mathrm{2}}{\left|s_{\mathrm{1}}\right|}^{{\mathit{\alpha }}_{\mathrm{1}}}sgn\left(s_{\mathrm{1}}\right)-c_{\mathrm{1}}{\dot{q}}_{\mathrm{1}}\\ +n_{\mathrm{11}}{h}_{\mathrm{1}}+n_{\mathrm{12}}{h}_{\mathrm{2}}+n_{\mathrm{13}}{h}_{\mathrm{3}}-d_{\mathrm{1}}\\ -k_{\mathrm{3}}{s}_{\mathrm{2}}-k_{\mathrm{4}}{\left|s_{\mathrm{2}}\right|}^{{\mathit{\alpha }}_{\mathrm{2}}}sgn\left(s_{\mathrm{2}}\right)-c_{\mathrm{2}}{\dot{q}}_{\mathrm{2}}\\ +n_{\mathrm{21}}{h}_{\mathrm{1}}+n_{\mathrm{22}}{h}_{\mathrm{2}}+n_{\mathrm{23}}{h}_{\mathrm{3}}-d_{\mathrm{2}}\end{array}\right].\end{array}\end{array}$$

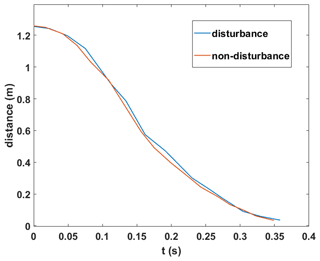
Using the disturbance control input Eq. (15) and the non-disturbance control input Eq. (8) model, respectively, the swing motion is carried out from the initial position ($x=-\mathrm{0.5}$ m, y=0 m) to the target position (x=0.75 m, y=0.15 m). During the swing period from opening the gripper to closing the gripper, the simulation experiment records the distance from the gripper to the target position. By comparing the distance curve of the above two models, the effect of disturbance on the control scheme is obvious, as shown in Fig. 11. Under the disturbance term with A=5 and T=0.1, the recorded distance approaches zero; in other words, the gripper reaches the target position and completes the swing motion. Compared with the case without disturbance, when there is disturbance, the distance curve has a small range of fluctuations and is relatively stable overall. In addition, Fig. 11 shows that the distance takes a longer time to approach zero under disturbance. We can conclude that the proposed control algorithm is effective under disturbances.

Figure 11 The distance to the target point.

5 Conclusions

The main contribution of this paper is to apply the sliding-mode control to the swing motion of the brachiation robot. The sliding-mode control has robustness to the initial point, the target point, the action of the gripper, the uncertainties model and the motor torque limitation, which realizes the continuous swing of the robot on irregularly distributed bars. Besides, compared with the two-link structure as shown in Table 2, the three-link structure introduced in this paper improves the swing efficiency and increases the swing height of the brachiation robot. The simulation experiment in ROS-Gazebo shows that the robot completes the single swing motion to the target bar (x=0.75 m, y=0.15 m), and the swing efficiency reaches 75 %. Meanwhile, the robot carries out the continuous swing motion on irregularly distributed bars. Compared to evenly distributed bars, the positions of the irregularly distributed bars have changed by 0.2 m in the horizontal direction and by 0.1 m in the vertical direction. The simulation results show that the sliding-mode control and three-link structure significantly improve the robustness and swing efficiency of the brachiation robot. The direction for future work is to build the physical brachiation robot. To further verify the reliability of the controller, we will carry out the swing motion on the physical robot.