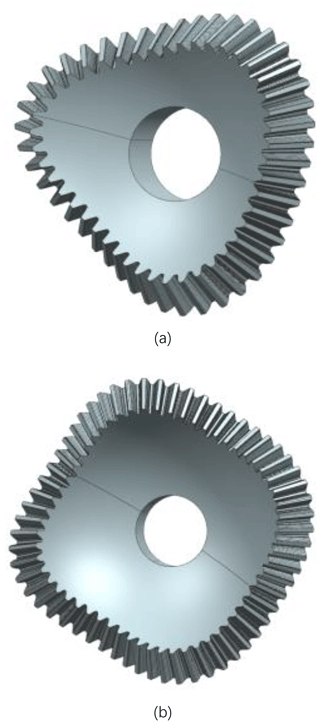
Synthesis of the base curves for n-lobed noncircular bevel gears

As a type of spatial transmission mechanism, noncircular bevel gears can transfer power and motion between two intersecting axes with variable transmission. In this paper, the relation of arc length is expressed by Angle in spatial polar coordinate system, utilizing the spherical triangle theorem, the parametric equations of base curves are established by applying arc length relation. Further, an example is given to verify whether pitch curves is concave on osculating circle of noncircular bevel gear section cone. Similarly, this example illustrates the cause of the mutation for the base curves.

1 Introduction

Gear is the most widely used transmission part in mechanical field. Cylindrical gear can achieve fixed transmission ratio between two fixed shafts while bevel gear can achieve fixed transmission ratio of intersecting shafts. Variable transmission ratio is need in more occasions, examples of its application include printing machinery, textile machinery, liquid flow meter, hydraulic motor and so on (Fan, 2018). Olsson (1953) system introduced noncircular gear in his book in 1953.

While in other case, the machine needs to achieve the transmission of intersecting shaft with variable transmission ratio. As a type of spatial transmission mechanism, noncircular bevel gears can transfer power and motion between two intersecting axes with variable transmission, as shown in Fig. 1. Noncircular bevel gear integrates the advantages of noncircular gear and bevel gear, and it has a broad application prospect. However, there are relatively few studies on noncircular bevel gears both at home and abroad. Many researches have studied tooth profile equation and 3D modeling of noncircular bevel gear (Zheng et al., 2016; Shi et al., 2013; Chen et al., 2014; Xia et al., 2008, 2014). The finite element analysis software ANSYS was used to simulate contact stress and mechanical properties (Ke et al., 2018a, b). Jia et al. (2008a) took a more unique approach, adopting the space-plane-space research method to obtain an approximate solution of tooth profile curve. Determination results of the processing method of noncircular bevel gears are reported in Jia et al. (2008b, c). Tooth profile shapes can be involute, cycloid, arc and other shapes, which directly affect the performance of gear (Meng et al., 2009). The intersecting line between the evolute surface of tooth profile surface and the spherical surface of noncircular bevel gear is spherical base curve. The curvature of tooth profile can be estimated by studying base curve of tooth profile, and the limit condition without undercut of noncircular bevel gear is analyzed. Since the left and right tooth profiles of noncircular bevel gears are asymmetric, the spherical base curves of their tooth profiles are different. For noncircular bevel gears, if the transmission ratio function and the included angle between two axes are given, the tooth profile curve and its base curve can be determined after determining the pitch curve and tooth shape of cutting tool. Figliolini et al. (2016) proposed the base curves of involute cylindrical gears according to Aronhold's first theorem and the return circle. In the latest research, utilizing the spherical triangle theorem and meshing principle, a formulation of the tooth profile of a noncircular bevel gear is deduced using an analytic method by Shi et al. (2020).

Figure 1 3D modeling of noncircular bevel gears. (a) 3-lobed, (b) 4-lobed.

2 The Angle is used to represent the arc length

Referring to Fig. 2, the polar angle of pitch curve corresponding to intersection angle is λ_l and λ_r, which is between the great arc of sphere and tooth profile on the left and right sides. The pitch circle 1 of bevel gear cutter and the pitch curve 2 of noncircular bevel gear make tangential pure roll, and and are normal arcs of intersection line, formed by normal plane and sphere at meshing point of tooth profile on left and right side of cutter.

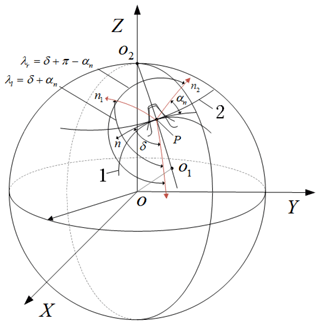
Figure 2 The intersection Angle between the normal arcs of tooth profile. 1 – Bevel gear cutter pitch circle of noncircular bevel gear. 2 – Noncircular bevel gear pitch curve of noncircular bevel gear.

When cutting, no matter where tooth profile of tool and noncircular bevel gear contact, the intersection angle between tooth profile normal arc and the intersecting line of pitch curve at common tangent plane of node P and spherical surface equals to the tool profile angle α_n. At mesh node P, the polar angle of pitch curve corresponds to the intersection angle between the great arc of sphere surface and tooth profile normal arc and on left and right sides, and the intersection angle are λ_l and λ_r.

The polar angle of pitch curve corresponding to intersection angle between the great arc of sphere surface and the normal arc of tooth profile on left and right sides, and therefore

$$\begin{array}{}\text{(1)}& \left\{\begin{array}{l}{\mathit{\lambda }}_{\mathrm{l}}=\mathit{\delta }+{\mathit{\alpha }}_n\\ {\mathit{\lambda }}_{\mathrm{r}}=\mathit{\delta }+\mathit{\pi }-{\mathit{\alpha }}_n\end{array}\right.,\end{array}$$

α_n: Tool profile angle, φ: Pitch curve polar angle, δ: Tangent azimuth angle, $\tan \mathit{\delta }=\frac{\sin \mathit{\phi }}{{\mathit{\phi }}^{\prime }\left(\mathit{\theta }\right)}$.

The polar angle φ of the pitch curve of noncircular bevel gear changes periodically with perigon θ, the tangent azimuth δ of each point on the corresponding pitch curve also changes periodically. Therefore, the polar angle at the intersection of tooth profile normal arc and pitch curve on the left and right sides of gear, corresponding to the intersection angle of sphere great arc, is also variate, while the difference between λ and δ is constant.

The spherical base curves of left and right tooth profiles of noncircular bevel gears are different. The relation between the pitch curve of noncircular bevel gear and the tooth profile base curves are illustrated in Fig. 3. Among then, point $A_i^{\prime }$ on the spherical base curve of pitch curve is the projection of osculating circle center (curvature circle) at point $P_i^{\prime }$ on sphere pitch curve. Utilizing the law of spherical cosines, we can get the osculating bevel angle $P_i^{\prime }{A}_i^{\prime }={\mathit{\rho }}^{\prime }$. The normal plane of tooth profile curve intersects with the sphere at arc $P_i^{\prime }{C}_i^{\prime }$, $P_i^{\prime }{C}_i^{\prime }$ intersects with the tooth profile curve at point $P_i^{\prime }$, and $P_i^{\prime }{C}_i^{\prime }$ is tangent to the spherical base curve of tooth profile curve at point $C_i^{\prime }$. Arc $P_i^{\prime }{A}_i^{\prime }$ is in the normal plane of pitch curve, and $P_i^{\prime }{A}_i^{\prime }$ is normal arc. Arcs $A_i^{\prime }{C}_i^{\prime }$, $C_i^{\prime }{P}_i^{\prime }$ and $P_i^{\prime }{A}_i^{\prime }$ form spherical triangle $C_i^{\prime }{P}_i^{\prime }{A}_i^{\prime }$.

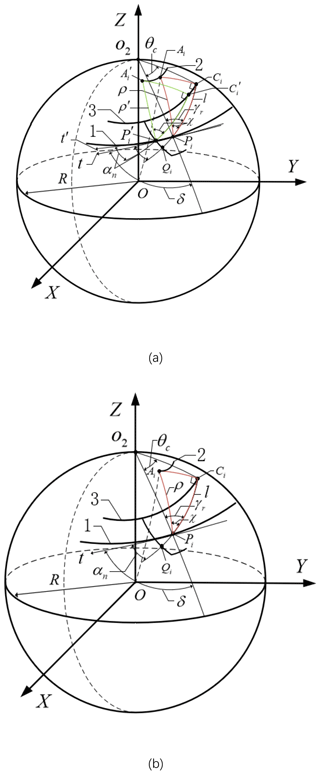
Figure 3 Relationship between pitch curve and base curves of tooth profile. (a) On the left side of the tooth profile. (b) The right side of the tooth profile. 1 – Pitch curve of circular bevel gear. 2 – Spherical base curve of pitch curve. 3 – Spherical base curve of tooth profile curve.

$P_i^{\prime }{A}_i^{\prime }$ is perpendicular to P_it, and the intersection angle between each normal arc of the tooth profile arc family of noncircular bevel gear and the tangent arc of its corresponding pitch curve is the tooth angle α_n of the cutter, so $\mathrm{\angle }{C}_i^{\prime }{P}_i^{\prime }{A}_i^{\prime }=\mathit{\chi }=\frac{\mathit{\pi }}{\mathrm{2}}-{\mathit{\alpha }}_n$. When an arc $P_i^{\prime }{A}_i^{\prime }$ of a spherical triangle $C_i^{\prime }{P}_i^{\prime }{A}_i^{\prime }$ rolls along the spherical base curve of pitch curve, the normal arc family of tooth profile curve can be reproduced. Direction of velocity at any point on tooth profile normal arc is perpendicular to the instantaneous radius of rotation around point $A_i^{\prime }$, and the velocity direction of tangent point $C_i^{\prime }$ on spherical base curve of tooth profile curve and normal arc should follow the normal direction of tooth profile, so $P_i^{\prime }{C}_i^{\prime }\perp A_i^{\prime }{C}_i^{\prime }$, and the trajectory of point $C_i^{\prime }$ is the spherical base curve of noncircular bevel gear tooth profile curve. Assume that spherical triangle $C_i^{\prime }{P}_i^{\prime }{A}_i^{\prime }$ rolls an angle around the base curve of its pitch curve to form triangle C_iP_iA_i. Similarly, P_iC_i⊥A_iC_i, and point C_i is also on the spherical base curve of tooth profile curve, forming a spherical involute tooth profile curve.

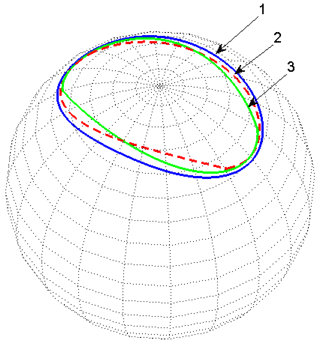
Figure 4 Spherical base curve of tooth profile curve of second order elliptic bevel gear. 1 – Pitch curve. 2 – Spherical base curve of right tooth profile. 3 – Spherical base curve of left tooth profile.

Figure 5 Spherical base curve of tooth profile curve of high order noncircular bevel gear (Small eccentricity). (a) ϕ=3^∘, λ=74^∘, n=3. (b) ϕ=1^∘, λ=74^∘, n=4. 1 – Pitch curve. 2 – Spherical base curve of right tooth profile.

3 Spherical base curve equation of tooth profile curve

In spherical right triangle A_iP_iC_i, according to the cotangent theorem of spherical triangles, the length of P_iC_i is given by:

$$\begin{array}{}\text{(2)}& l=\arctan \left(\sin {\mathit{\alpha }}_n\cdot \tan \mathit{\rho }\right),\end{array}$$

The projection of osculating circle center of the noncircular bevel gear pitch curve on sphere is not the projection of its rotation center. In the spherical triangle ${\mathit{\gamma }}_{\mathrm{r}}={\mathit{\lambda }}_{\mathrm{r}}-\mathit{\pi }=\mathit{\delta }-{\mathit{\alpha }}_n$, the perigon θ_c and polar angles φ_c of spherical polar coordinates at any point on the spherical base curve of right tooth profile are obtained by using the cosine theorem of spherical triangles, and

$$\begin{array}{}\text{(3)}& \left\{\begin{array}{l}{\mathit{\phi }}_{\mathrm{c}}=\arccos \left[\cos \mathit{\phi }\cdot \cos l+\sin \mathit{\phi }\cdot \sin l\cdot \cos {\mathit{\gamma }}_{\mathrm{r}}\right]\\ {\mathit{\theta }}_{\mathrm{c}}=\arccos \left(\frac{\cos l-\cos \mathit{\phi }\cdot \cos {\mathit{\phi }}_{\mathrm{c}}}{\sin \mathit{\phi }\cdot \sin {\mathit{\phi }}_{\mathrm{c}}}\right)\end{array}\right.,\end{array}$$

Any point on the noncircular bevel gear pitch curve corresponds to the point on the spherical base curve of right tooth profile curve, which the coordinates can be calculated according to Eqs. (2) and (3), and its trajectory forms the spherical base curve of the right tooth profile. Similarly, the spherical base curve equation of the left tooth profile curve can be obtained, and

$$\begin{array}{}\text{(4)}& {\mathit{\gamma }}_{\mathrm{l}}=\mathit{\pi }-{\mathit{\lambda }}_{\mathrm{l}}=\mathit{\pi }-\mathit{\delta }-{\mathit{\alpha }}_n,\end{array}$$

According to the spherical triangle theorem, the Angle γ between the rotation axis of the osculating circle cone and the rotation axis of the noncircular bevel gear satisfies:

$$\begin{array}{}\text{(5)}& \cos \mathit{\gamma }=c\mathrm{os}\mathit{\phi }\cdot \cos \mathit{\rho }+\sin \mathit{\rho }\cdot \sin \mathit{\phi }\cdot \cos \mathit{\varsigma },\end{array}$$

Then, check concavity of pitch curve:

$$\begin{array}{}\text{(6)}& \tan \mathit{\rho }=-{\displaystyle \frac{{\left[{\sin }^{\mathrm{2}}\mathit{\phi }+{\mathit{\phi }}^{\prime \mathrm{2}}\left(\mathit{\theta }\right)\right]}^{\frac{\mathrm{3}}{\mathrm{2}}}}{\cos \mathit{\phi }\cdot {\sin }^{\mathrm{2}}\mathit{\phi }+\mathrm{2}\cos \mathit{\phi }\cdot {\mathit{\phi }}^{\prime \mathrm{2}}\left(\mathit{\theta }\right)-\sin \mathit{\phi }\cdot {\mathit{\phi }}^{\prime \prime }\left(\mathit{\theta }\right)}}.\end{array}$$

If tan ρ<0, pitch curve is convex. If tan ρ>0, pitch curve is concave.

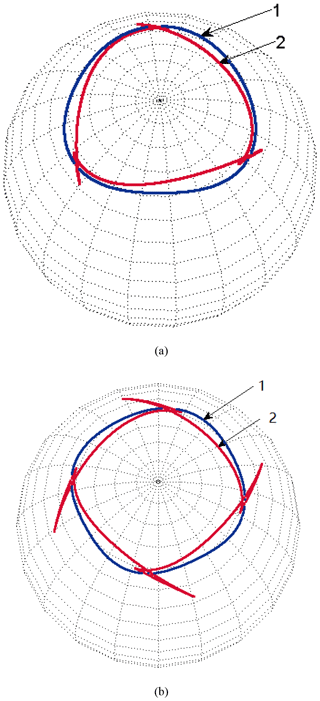
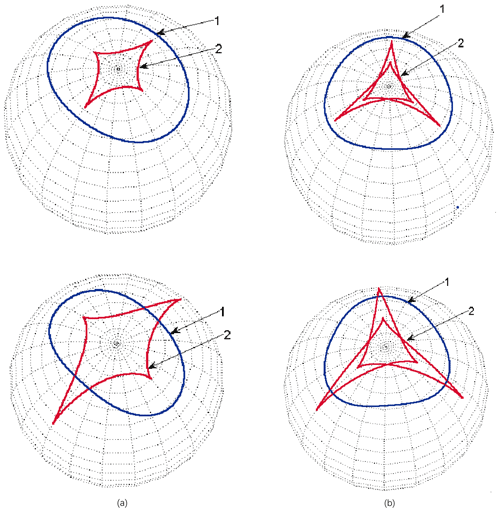
Figure 6 Spherical base curve of tooth profile curve of high order noncircular bevel gear (Large eccentricity). (a) ϕ=5^∘, λ=74^∘, n=3. (b) ϕ=3^∘, λ=74^∘, n=4. 1 – Pitch curve. 2 – Spherical base curve of right tooth profile.

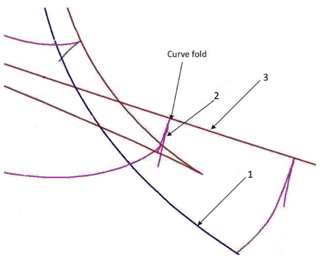
Figure 7 Tooth profile produces prismatic phenomenon. 1 – Pitch curve. 2 – Right tooth profile curve. 3 – Spherical base curve of right tooth profile.

Figure 8 Spherical base curve of pitch curve. (a) n=2, top: ϕ=10^∘, λ=74^∘, bottom: ϕ=18^∘, λ=74^∘. (b) n=3, top: ϕ=5^∘, λ=74^∘, bottom: ϕ=7^∘, λ=74^∘. 1 – Pitch curve. 2 – Spherical base curve of pitch curve.

4 Examples

Spherical base curves of left and right tooth profiles of noncircular bevel gears are related to various rules of order and pitch curves. Corresponding to the noncircular bevel gears without concave pitch curves, the spherical base curve of tooth profiles should be included in the pitch curves. When the pitch curve is concave, the concave point is equivalent to the internal gear. Therefore, the spherical base curve of the corresponding point on the tooth profile curve should be outside the pitch curve.

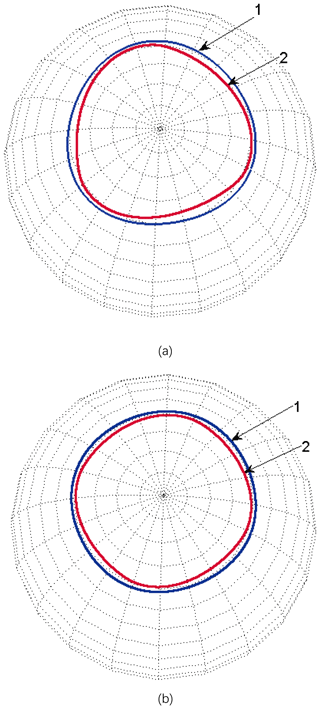
The spherical base curves of the left and right tooth profiles of second-order elliptic bevel gears are illustrated in Fig. 4. Equations (5) and (6) can verify that the pitch curve has no concave. As can be seen from the figure, the spherical base curve of left and right tooth profile is not the spherical equidistance line of pitch curve, so different tooth profile curves are formed.

The spherical base curves of the tooth profile curves of the third and fourth order noncircular bevel gears are illustrated in Fig. 5. According to Eq. (4), the pitch curve is verified to have no concave. The spherical base curve of tooth profile curve is inside the pitch curve with small eccentricity.

For different λ and ϕ, the shape of spherical base curve of left and right tooth profile curve is different. With the increase of eccentricity, mutation occur in the spherical base curve of tooth profile curve, as shown in Fig. 6. In addition, the mutation is also related to the order of the gear. With the increase of the order, the extremely small eccentricity change will also cause mutation of base curve.

Since there is a correspondence between the involute tooth profile curve and the spherical curve, when the spherical base curve changes suddenly, the tooth profile curve fold, meanwhile the curve has no concave at this time, as shown in Fig. 7. There is a pair of noncircular bevel gears engaged, the range of transmission ratio fluctuations is proportional to the relative curvature between tooth surfaces. When the eccentricity of spherical ellipse (pitch curve) increases, the variation range of its velocity ratio increases and the relative curvature between tooth surfaces increases rapidly. It folds on the tooth surface near the dedendum.

The relation between spherical base curves of noncircular bevel gear pitch curves and eccentricity of pitch curves are illustrated in Fig. 8.

5 Conclusions

In this paper, the noncircular bevel gear is studied in spatial polar coordinate system. The relation of arc length in space is expressed by Angle. The mathematical model of base curves is established by applying arc length relation. An example illustrates the cause of the mutation for the base curves.

Above all, the mutation of tooth profile base curve is related to eccentricity but not to the convexity of noncircular bevel gear pitch curve. The eccentricity of spherical ellipse (pitch curve) increases and flattens horizontally when achieving the transmission ratio with large fluctuation range. Since the intersection angle between the tangent arc of pitch curve and the tooth profile arc is tooth profile angle of the cutter, the osculating conical angle of pitch curve tends to be infinite, which shows mutation of the spherical base curve of tooth profile curve. When the base curve of tooth profile mutates, it is not suitable to draw involute tooth profile.