Stress state of a polygonal plate having a central circular hole with two linear cracks in the small physical non-linear condition

In this study, the stress state of a polygonal plate having a central circular hole with two linear cracks was considered. External forces were applied to the contours of polygonal plate and internal forces were applied to the contours of the circular hole. Conformal mapping function, initially developed by Kuliyev, was used to the make stress analysis of the polygonal plate in physical non-linear statement. As a result, stress concentrations were determined by using conformal mapping function at the end points of cracks. Critical loads where fracture began were defined for different loads. Analytical results of solutions were compared and found to be in agreement with the numerical results in the literature.

1 Introduction

In recent years, solution of physical non-linear problems in the fields of physics and engineering that cannot be solved through linearization of assumptions and principal equations (such as stress-strain relationship), has necessitated making improvements in classical elasticity theory, which in turn has led to the development of non-linear elasticity theory.

All assumptions and resulting errors mentioned in elasticity theory up to date have shown that, there is insufficient information on the new variants of non-linear elasticity theory. In classic elasticity theory, linearization is mainly assumed to be in two directions. The first one is the geometry of a deformable body and the other is physical properties of material (relationship of stress-strain, i.e. the Hooke's law).

Since classical elasticity theory cannot be applied for non-linear materials, Muskhelishvili (1962) developed a method to solve the stress states of non-linear materials, in which complex variable functions are used to make stress analysis.

Stress concentration around a hole in an infinite plate subjected to a uniform load was investigated by Batista (2011) using Muskhelishvili's (1962) conformal mapping complex variable method. Pan et al. (2013) performed the stress analysis of a finite plate having a rectangular hole subjected to uniaxial tension using a modified form of Muskhelishvili's (1962) conformal mapping function. Sharma (2012) examined the stress distribution around polygonal holes in an infinite plate subjected to arbitrary biaxial in-plane loadings at infinity also by using Muskhelishvili's (1962) complex variable method. In his study, plane stress finite models were prepared in ANSYS and the results were compared with those of the complex variable method (Sharma, 2012). Sharma (2015) obtained a general solution in hypocycloidal hole with cusps in infinite anisotropic plate in order to calculate the stress intensity factors by using Muskhelishvili's (1962) complex variable method. Kuliyev (2003), on the other hand, investigated the stress-strain state of a polygonal plate weakened by a central elliptic hole with two linear cracks by using modified conformal mapping function. Kuliyev (2010) also obtained the solution for critical angular velocity in polygonal plate weakened by elliptic holes using a modified version of conformal mapping function.

In this paper, stress components of a polygonal plate having central circular hole with two linear cracks were obtained. Conformal mapping function which was developed by the author (Kuliyev, 1991, 2017) was used to determine the stress intensity factors for complex geometries. In this work, a complex geometry with additional two linear cracks is solved for the first time using Kuliyev's mapping function, and the results were compared with the literature findings which proved to be in good agreement.

2 Problem statement and solution methods

Physical law of deformability, i.e., relationship of stress-strain components is explained in two ways:

1. General functional relationship of stress and strain (between two different power symmetric tensor components) (Kauderer, 1961).

2. Inclusion of deformation energy function into elasticity potential (Globenko, 1974).

As mentioned above, determination of real physical relationships between stress-strain components and solution of some complex problems in engineering constitute the essence of non-linear elasticity theory.

As reported in the literature (Kuliyev, 1991, 2001; Amenzade, 1976; Berezhnitskii et al., 1919; Sherman, 1947, 1951) Airy Stress Function F⁽ⁿ⁾ is determined by two analytic functions, namely φ(z) and ψ(z) in linear elasticity theory (plane problems)

$$\begin{array}{}\text{(1)}& F^{\left(\mathrm{0}\right)}=\text{Re}\left[\stackrel{\mathrm{‾}}{z}\cdot \mathit{\phi }\left(z\right)+\int \mathit{\psi }\left(z\right)\mathrm{d}z\right]\end{array}$$

where, Re shows the real part of the expression in bracket.

The functions of elasticity theory named as φ(z) and ψ(z) in finite or infinite form of bodies (plate, cylinder, prism and etc.) and connected domains are taken as follows (Kuliyev, 1991, 2001; Amenzade, 1976; Berezhnitskii et al., 1919; Sherman, 1947, 1951).

2.1 For finite doubly – connected domains

The regular functions φ(z) and ψ(z) are as follows (Kuliyev, 1991, 2001; Amenzade, 1976; Sherman, 1947, 1951).

$$\begin{array}{}\text{(2)}& \begin{array}{rl}\mathit{\phi }\left(z\right)& =\sum _{k=\mathrm{1}}^{\mathrm{\infty }}{\mathit{\alpha }}_k\cdot {\mathit{\xi }}_{\mathrm{1}}^{-k}+\sum _{k=\mathrm{0}}^{\mathrm{\infty }}{A}_k{\left({\displaystyle \frac{z}{A}}\right)}^k\\ \mathit{\psi }\left(z\right)& =\sum _{k=\mathrm{1}}^{\mathrm{\infty }}{\mathit{\beta }}_k\cdot {\mathit{\xi }}_{\mathrm{1}}^{-k}+\sum _{k=\mathrm{0}}^{\mathrm{\infty }}{B}_k{\left({\displaystyle \frac{z}{A}}\right)}^k\end{array}\end{array}$$

where ξ₁ is the function of ξ=χ(z), inverse function (z=ω(ξ₁)) of which conforms L₁ inner contour around the unit circle in Fig. 1 (Kuliyev, 1991, 2001).

Figure 1 A hexagonal cross-section under interior and exterior pressure.

The coefficients A_k and B_k of analytic functions are as follows:

$$\begin{array}{}\text{(3)}& \begin{array}{rl}{A}_k& =\sum _{n=k}^{\mathrm{\infty }}{}^{\ast }{a}_n^{\left(k\right)}\cdot a_{\frac{n-k}{q}}^{\left(n\right)}\\ B_k& =\sum _{n=k}^{\mathrm{\infty }}{}^{\ast }{b}_n\cdot a_{\frac{n-k}{q}}^{\left(n\right)}\end{array}\end{array}$$

The coefficient $a_n^{\left(k\right)}$ in Eq. (3) is found for total contour and given in table form in (Kuliyev, 2017). The symbol ^∗ indicates the indices in series Eq. (3) with increment q. We assume that contours L₁ and L₂ are concentric in doubly connected domains.

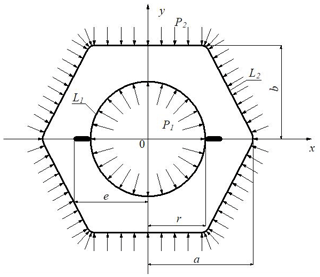
Here, F⁽⁰⁾ is the Airy stress function in zero approximation. The function F⁽⁰⁾ is given by the known formula (the plate is under the influence of internal p₁ and external pressure p₂ equi-distributed hydrostatic pressure in Fig. 1) for polygonal doubly connected plates (Kuliyev, 1991, 2001; Muskhelishvili, 1962; Amenzade, 1976; Berezhnitskii et al., 1919).

In the considered case, the boundary conditions are as follows in zero approximation:

• on the inner contour L₁ (with r radius circle and two linear cracks)

  $$\begin{array}{}\text{(4)}& {\mathit{\sigma }}_{\mathit{\rho }}^{\left(\mathrm{0}\right)}\left|{}_{\mathit{\rho }=t_{\mathrm{1}}}\right.=-P_{\mathrm{1}}\end{array}$$

  on the outer contour L₂ (equilateral polygon)

  $$\begin{array}{}\text{(5)}& {\mathit{\sigma }}_{\mathit{\rho }}^{\left(\mathrm{0}\right)}\left|{}_{\mathit{\rho }=t_{\mathrm{2}}}\right.=-P_{\mathrm{2}}\end{array}$$

For the next approximations (the first and the second), the boundary conditions are as follows:

$$\begin{array}{}\text{(6)}& {\mathit{\sigma }}_{\mathit{\rho }}^{\left(\mathrm{1}\right)}\left|{}_{\mathit{\rho }=t_{\mathrm{1}}}=\mathrm{0}\right.,{\mathit{\sigma }}_{\mathit{\rho }}^{\left(\mathrm{1}\right)}\left|{}_{\mathit{\rho }=t_{\mathrm{2}}}=\right.\mathrm{0}\end{array}$$

In Eqs. (4), (5), (6), t₁ and t₂ are the affixes of the points of the contours $L_j\left(j=\mathrm{1};\mathrm{2}\right)$, respectively. The function F⁽¹⁾ is found from the solution of Eq. (1).

$$\begin{array}{}\text{(7)}& \mathrm{\Delta }\mathrm{\Delta }{F}^{\left(\mathrm{2}\right)}+L_{\mathrm{2}}\left[F^{\left(\mathrm{0}\right)},F^{\left(\mathrm{1}\right)}\right]=\mathrm{0}\end{array}$$

The solution of Eq. (7) is found from the sum of general solution ΔΔF⁽¹⁾=0 of the first differential equation $\left(F_{\mathrm{gen}.}^{\left(\mathrm{1}\right)}\right)$ and the special solution $\left(F_{\mathrm{spec}.}^{\left(\mathrm{1}\right)}\right)$ of the mentioned differential equation.

$$\begin{array}{}\text{(8)}& F^{\left(\mathrm{1}\right)}=F_{\mathrm{gen}.}^{\left(\mathrm{1}\right)}+F_{\mathrm{spec}.}^{\left(\mathrm{1}\right)}\end{array}$$

It is known that the general solution of the homogeneous differential equation ΔΔF⁽¹⁾=0 is taken in the following way (in the general case):

$$\begin{array}{}\text{(9)}& F_{\mathrm{gen}.}^{\left(\mathrm{1}\right)}=c_{\mathrm{1}}\cdot \ln \mathit{\rho }+c_{\mathrm{2}}\cdot {\mathit{\rho }}^{\mathrm{2}}\end{array}$$

Note that, if we pass to polar (ρ,θ) coordinates, we get the following differential equation for the function F⁽¹⁾ (Kuliyev, 2017).

$$\begin{array}{}\text{(10)}& \mathrm{\Delta }\mathrm{\Delta }{F}^{\left(\mathrm{1}\right)}=\sum _{k=\mathrm{1}}^{\mathrm{\infty }}{\mathit{\rho }}^{-k}\cdot V_{\mathrm{1}}\left(k\right)+\sum _{k=\mathrm{0}}^{\mathrm{\infty }}{\mathit{\rho }}^k\cdot V_{\mathrm{2}}\left(k\right)\end{array}$$

In this equation, the quantities V₁(k) and V₂(k) are algebraic sums of the same power terms of the variable p (for the fixed θ angle). The special solution $F_{\mathrm{spec}.}^{\left(\mathrm{1}\right)}$ is found from fourfold integration of Eq. (10) in the following way (Kuliyev, 1991, 2001):

$$\begin{array}{}\text{(11)}& \begin{array}{rl}{F}_{\mathrm{spec}.}^{\left(\mathrm{1}\right)}& =\sum _{k=\mathrm{0}}^{\mathrm{\infty }}{\mathit{\rho }}^{-k+\mathrm{4}}\cdot \mathit{\alpha }\cdot V_{\mathrm{1}}\left(k\right)\\ & +\sum _{k=\mathrm{0}}^{\mathrm{\infty }}\mathit{\beta }\cdot {\mathit{\rho }}^{k+\mathrm{4}}\cdot V_{\mathrm{2}}\left(k\right)\end{array}\end{array}$$

where

$$\begin{array}{}\text{(12)}& \begin{array}{rl}\mathit{\alpha }& ={\left[{\left(\mathrm{4}-k\right)}^{\mathrm{2}}\cdot {\left(\mathrm{2}-k\right)}^{\mathrm{2}}+{\mathit{\alpha }}_{\mathrm{1}}+{\mathit{\alpha }}_{\mathrm{2}}\right]}^{-\mathrm{1}}\\ \mathit{\beta }& ={\left[{\left(k+\mathrm{4}\right)}^{\mathrm{2}}\cdot {\left(\mathrm{2}+k\right)}^{\mathrm{2}}+{\mathit{\beta }}_{\mathrm{1}}+{\mathit{\beta }}_{\mathrm{2}}\right]}^{-\mathrm{1}}\end{array}\end{array}$$

The unknown coefficients c₁ and c₂ in Eq. (9) are found from the boundary conditions of the considered problem (stress-strain state of a doubly-connected polygonal plate subjected to equi-distributed internal pressure p₁ and external pressure p₂) (Kuliyev, 1991, 2001).

If on the L₁ inner contour

$$\mathit{\rho }=t_{\mathrm{1}}\text{ then }{\mathit{\sigma }}_{\mathit{\rho }}^{\left(\mathrm{1}\right)}=\mathrm{0}$$

If on the L₂ external contour

$$\begin{array}{}\text{(13)}& \mathit{\rho }=t_{\mathrm{2}}=A\text{ then }{\mathit{\sigma }}_{\mathit{\rho }}^{\left(\mathrm{1}\right)}=\mathrm{0}\end{array}$$

After finding the expression $F(\mathit{\rho },\mathit{\theta },\mathit{\lambda }t)=F^{\left(\mathrm{0}\right)}\left(\mathit{\rho },\mathit{\theta }\right)+\mathit{\lambda }{F}^{\left(\mathrm{1}\right)}\left(\mathit{\rho },\mathit{\theta }\right)+{\mathit{\lambda }}^{\mathrm{2}}\cdot F^{\left(\mathrm{2}\right)}\left(\mathit{\rho },\mathit{\theta }\right)+\mathrm{\dots }$ for the stress components σ_ρ and σ_θ we get the following expressions in the form of the following series:

$$\begin{array}{}\text{(14)}& \begin{array}{rl}{\mathit{\sigma }}_{\mathit{\rho }}& ={\mathit{\sigma }}_{\mathit{\rho }}^{\left(\mathrm{0}\right)}+\mathit{\lambda }\cdot {\mathit{\sigma }}_{\mathit{\rho }}^{\left(\mathrm{1}\right)}+{\mathit{\lambda }}^{\mathrm{2}}\cdot {\mathit{\sigma }}_{\mathit{\rho }}^{\left(\mathrm{2}\right)}+\mathrm{\dots }\\ {\mathit{\sigma }}_{\mathit{\theta }}& ={\mathit{\sigma }}_{\mathit{\theta }}^{\left(\mathrm{0}\right)}+\mathit{\lambda }\cdot {\mathit{\sigma }}_{\mathit{\theta }}^{\left(\mathrm{1}\right)}+{\mathit{\lambda }}^{\mathrm{2}}\cdot {\mathit{\sigma }}_{\mathit{\theta }}^{\left(\mathrm{2}\right)}+\mathrm{\dots }\\ {\mathit{\tau }}_{\mathit{\rho }\mathit{\theta }}& ={\mathit{\tau }}_{\mathit{\rho }\mathit{\theta }}^{\left(\mathrm{0}\right)}+\mathit{\lambda }\cdot {\mathit{\tau }}_{\mathit{\rho }\mathit{\theta }}^{\left(\mathrm{1}\right)}+{\mathit{\lambda }}^{\mathrm{2}}\cdot {\mathit{\tau }}_{\mathit{\rho }\mathit{\theta }}^{\left(\mathrm{2}\right)}+\mathrm{\dots }\end{array}\end{array}$$

The obtained general solution is demonstrated by the numerical examples.

2.2 Numerical Results

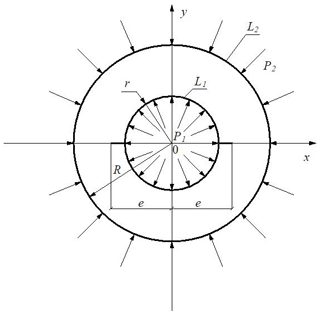
2.2.1 Stress state of a cylinder made of small physical nonlinear material and possessing an annular hole and two linear cracks

In linear elasticity theory, this problem was solved completely (within Hooke's law). Therefore, here we give only the results obtained in Kuliyev (1991, 2001).

Figure 2 Hollow round cylinder under interior and exterior pressure.

The ratio of the main measures of the cross section is given in two variants (Fig. 2):

• Variant I: $r/R=\mathrm{0.5}$; e=0.6 R; l=0.1 R

• Variant II: $r/R=\mathrm{0.7}$; e=0.8 R; l=0.1 R.

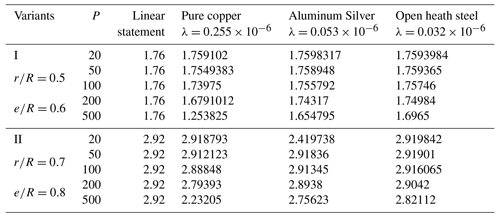
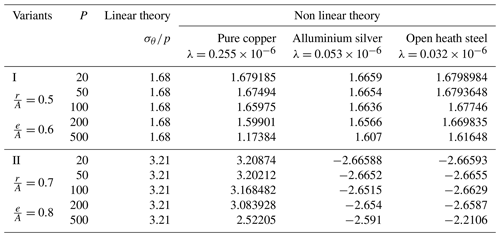
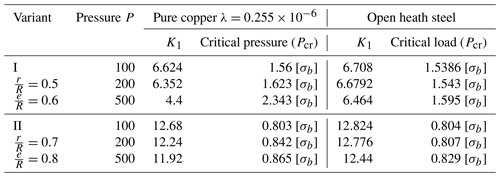
The stresses ${\mathit{\sigma }}_{\mathit{\rho }}^{\left(\mathrm{0}\right)}$ and ${\mathit{\sigma }}_{\mathit{\theta }}^{\left(\mathrm{0}\right)}$ found from characteristic points of the section (as tangential stresses τ_ρθ are too small, accepted τ_ρθ≈0) are given in Table 1. Stress intensities and critical stress values are given in Table 2.

At the most critical point of the section (at the end points of the cracks: $z=\pm e)$, we get the following values of $\mathrm{10}{K}_{\mathrm{1}}/p_{\mathrm{1}}\sqrt{l}$ for the stress intensity factor K₁:

• 7.00 for variant I and

• 11.68 for variant II.

The following estimates are found for the critical value of the internal pressure p₁=p (i.e. fracture of the body-minimal stress for elongation of cracks):

• For variant I: $P_{\mathrm{cr}}=\mathrm{1},\mathrm{46}\left[{\mathit{\sigma }}_b\right]$

• For variant II: $P_{\mathrm{cr}}=\mathrm{0},\mathrm{883}\left[{\mathit{\sigma }}_b\right]$ (Table 2)

where technical ultimate stress [σ_b] (maximum stress of the material) is known from references (Kuliyev, 1991, 2001).

Table 1 Stress coefficient concentrations.

Table 2 Stress intensity (by $\mathrm{10}{K}_{\mathrm{1}}/P\sqrt{l}$) and critical value of stress.

After finding the functions φ(z) and ψ(z), within the linear elasticity theory (in zero approximation), the stress function $F^{\left(\mathrm{0}\right)}\left(x,y\right)=F^{\left(\mathrm{0}\right)}\left(\mathit{\rho },\mathit{\theta }\right)$ is found by Eq. (1). Then F⁽¹⁾(ρ,θ) is found from Eq. (10) of the stress function in the first approximation. According to the found expression of the stress function F⁽¹⁾(ρ,θ), the stress σ_θ found from the characteristic points of the section by means of Eq. (14) is given in and Fig. 3.

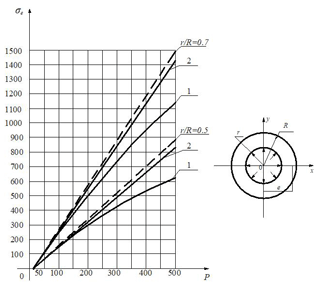
Figure 3 Hollow cylinder under interior pressure. The dotted line indicates a linear problem, the solid line a non-linear problem. (1: pure copper; 2: open heath steel).

Table 3 Stress concentrain of a hexogonal plate.

Table 4 Stress intensity coefficient ($\mathrm{10}{K}_{\mathrm{1}}/\mathit{\P }\sqrt{l}$) and critical value of load (P_cr) (hexagonal cylinder).

2.2.2 Stress state of a hexagonal plate with annular hole and two linear cracks in physical non-linear statement

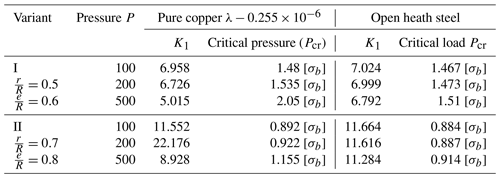
The solution of this problem in linear elasticity theory is known from references (Kuliyev, 1991, 2001). The stresses $\left({\mathit{\sigma }}_{\mathit{\theta }}^{\left(\mathrm{0}\right)}\right)$ found at any point of a hexagonal plate are calculated for different variants (for different values of the ratio of cross section measures) and given in the table. The stress intensity factor (K₁) and critical value P_cr of internal pressure are found and given for each variant at the end of Tables 3 and 4 according to the stresses found at the end points of the linear cracks. The known expression of the function is taken into account in differential Eq. (10) obtained for the solution of physical non-linear problem and accordingly, the stress for different values of internal pressure P_cr at the most critical points $F^{\left(\mathrm{0}\right)}\left(x,y\right)=F^{\left(\mathrm{0}\right)}\left(\mathit{\rho },\mathit{\theta }\right)$ of the section are found and given in table form.

The following expressions were considered for the stresses at the tips of the cracks.

• Variant I: $r/A=\mathrm{0.5}$; $e/A=\mathrm{0.6}$; m=0.04; $b=\mathrm{1},\mathrm{922}$;

  $${\mathit{\sigma }}_{\mathit{\theta }}/p={\mathit{\sigma }}_{\mathit{\theta }/p}^{\left(\mathrm{0}\right)}+\mathit{\alpha }{\mathit{\sigma }}_{\mathit{\theta }}^{\left(\mathrm{1}\right)}/p=\mathrm{1.68}-\mathrm{9.2}\cdot \mathit{\alpha }\cdot p^{\mathrm{2}}$$

• Variant II: $r/A=\mathrm{0.7}$; $e/A=\mathrm{0.8}$; m=0.04; b=1.37r

  $${\mathit{\sigma }}_{\mathit{\theta }}/p={\mathit{\sigma }}_{\mathit{\theta }/p}^{\left(\mathrm{0}\right)}+\mathit{\alpha }{\mathit{\sigma }}_{\mathit{\theta }}^{\left(\mathrm{1}\right)}/p=\mathrm{3.21}-\mathrm{14.62}\cdot \mathit{\alpha }\cdot p^{\mathrm{2}}$$

  where

  $$\mathit{\alpha }=\mathit{\lambda }={\displaystyle \frac{g_{\mathrm{2}}k}{\left(\mathrm{3}K+G\right)G^{\mathrm{2}}}}=\mathrm{0.225}\times {\mathrm{10}}^{-\mathrm{6}}{\mathrm{cm}}^{\mathrm{4}}{\mathrm{kg}}^{-\mathrm{2}}$$

  for pure copper.

  $$\mathit{\alpha }=\mathit{\lambda }=\mathrm{0.032}\times {\mathrm{10}}^{-\mathrm{6}}{\mathrm{cm}}^{\mathrm{4}}{\mathrm{kg}}^{-\mathrm{2}}$$

  for open-hearth steel.

As indicated by the numerical results of both problems in physical non-linear statement, the maximal values of stresses are smaller than that of the linear statement (peak points of stress diagrams are smoothened) (Fig. 1).

2.2.3 Stress state of a thick-walled pipe (Lame problem) in small physical non-linear statement

In classic elasticity theory, the following formula is obtained for the stress function F⁽⁰⁾ (Kuliyev, 1991, 2001).

$$\begin{array}{}\text{(15)}& F^{\left(\mathrm{0}\right)}\left(\mathit{\rho },\mathit{\theta }\right)={\mathit{\beta }}_{\mathrm{1}}\cdot {\displaystyle \frac{{\mathit{\rho }}^{\mathrm{2}}}{r^{\mathrm{2}}}}+d_{\mathrm{1}}\cdot r\cdot \ln \mathit{\rho }\end{array}$$

When the pipe is under the internal pressure p₁ and external hydrostatic pressure p₂, the coefficients β₁ and d₁ are determined by the following expressions (Kuliyev, 1991, 2001).

$$\begin{array}{}\text{(16)}& {\mathit{\beta }}_{\mathrm{1}}={\displaystyle \frac{r}{\mathrm{2}}}\cdot {\displaystyle \frac{p_{\mathrm{1}}\cdot r^{\mathrm{2}}-p_{\mathrm{2}}\cdot R^{\mathrm{2}}}{R^{\mathrm{2}}-r^{\mathrm{2}}}};d_{\mathrm{1}}={\displaystyle \frac{r^{\mathrm{2}}{R}^{\mathrm{2}}\cdot \left(p_{\mathrm{2}}-p_{\mathrm{1}}\right)}{\left(R^{\mathrm{2}}-r^{\mathrm{2}}\right)\cdot r}}\end{array}$$

if the Eq. (16) is written in Eq. (15);

$$\begin{array}{}\text{(17)}& \begin{array}{rl}{F}^{\left(\mathrm{0}\right)}\left(\mathit{\rho },\mathit{\theta }\right)& ={\displaystyle \frac{r^{\mathrm{2}}{R}^{\mathrm{2}}\cdot \left(p_{\mathrm{2}}-p_{\mathrm{1}}\right)}{R^{\mathrm{2}}-r^{\mathrm{2}}}}\cdot \ln \mathit{\rho }\\ & +{\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}{\displaystyle \frac{p_{\mathrm{1}}\cdot r^{\mathrm{2}}-p_{\mathrm{2}}\cdot R^{\mathrm{2}}}{R^{\mathrm{2}}-r^{\mathrm{2}}}}{\mathit{\rho }}^{\mathrm{2}}\end{array}\end{array}$$

The obtained expression completely coincides with the expressions obtained by Tsurpal (1962). The measures of thick-walled pipes (the ratio of radius R of external circle with radius r of internal circle) were given in two variants (pure copper, aluminum, bronze and open–heath steel were chosen as pipe's materials. The following expressions are obtained for stress concentration on the inner circle for the considered problem (Lame Problem).

• Variant I: ${\mathit{\sigma }}_{\mathit{\theta }}/p=\mathrm{1.666}-\mathrm{4.444}\cdot \mathit{\lambda }\cdot p^{\mathrm{2}}$; p₁=p

• Variant II: ${\mathit{\sigma }}_{\mathit{\theta }}/p=\mathrm{4.55}-\mathrm{25.3}\cdot \mathit{\lambda }\cdot p^{\mathrm{2}}$; p₁=p

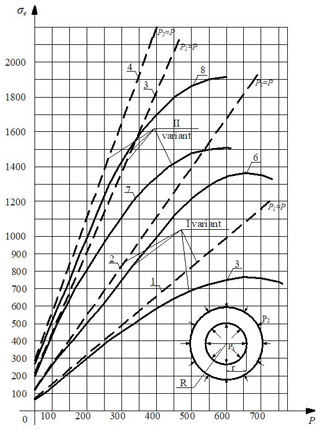
The stresses “σ_θ” were calculated for different values of internal pressure (p₁) ($\mathrm{20}\le p\le \mathrm{500}$) by means of the formulas given in graphic form in both variants (Fig. 4). In the graph, the straight line represents the problem in non–linear statement and the dotted line represents the problem in linear statement.

As seen in the tables, a decline at a rate of 0.1 % occurs for the values lower than 100 MPa, resulting in a negligible difference between linear and non-linear states. As for the values higher than or equal to 100 MPa, the stress difference between linear and nonlinear states is observed to be significantly high.

Figure 4 The Lame problem statement.

3 Conclusion

In this work, stress concentrations were determined by using conformal mapping function at the end points of cracks. Critical loads where fracture began were defined for different loads. Analytical results of solutions were compared and found to be in agreement with the numerical results in the literature. The obtained numerical calculations show that, as the nonlinearity of the materials increase, the stress distributions at the peak points of the stresses become more regular and physical–nonlinearity of the material smoothens the peaks of stresses by decreasing maximum value of stresses and moderately increasing minimum values. Also, the physical nonlinearity of the material decreases the stress concentration, thus decreasing the maximum stress at the inner points of the cross-section.

Appendix A: Nomenclature

K	bulk modulus
k(s0)	mean stress of s0 function
$g\left(t_{\mathrm{0}}^{\mathrm{2}}\right)$	intensity function
G	shear modulus
s0	expression for the reduced mean stress
E	Young modulus
F	Airy stress function
I1	strain tensor
L(n)	linear operator
λij	the coefficients which determine the physical properties of the considered materials
τ0	expression for intensity of the reduced tangential stresses
υ	Poisson ratio
χ	elongation function
Υ	shear strain function
εij	strain components
δij	the coefficients which determine the physical properties of the considered materials
σij	stress components
Δ	Laplace operator
φ(z), ψ(z)	analitic functions
q	symmetry axis number