Effect of compliant linkages on suspension under load

A numerical investigation is performed into the effects of rigid and compliant suspension linkages, respectively, on: the kinematics and handling performance of a lightweight electric vehicle (EV). CAE models of the front and rear suspension systems are first established based on the measured parameters of the target vehicle. The validity of the CAE models is confirmed by comparing the results obtained for the camber angle and kingpin inclination angle with those obtained mathematically using the vector loop method. CAE models are then performed using half-vehicle and whole-vehicle models. Quarter-vehicle simulations are then performed to compare the solutions obtained from the compliance and rigid-body models for the forces acting on the hardpoints of the two suspension systems under pothole impact conditions. Finally, whole-vehicle simulations are conducted using both the rigid-body model and the compliance model to evaluate the handling performance of the EV in impulse steering tests conducted at vehicle speeds of 40, 60 and 80 km h⁻¹, respectively. In general, the results show that the choice of a rigid-body model or a compliance model has a significant effect on the forces computed at some of the hardpoints in the front and rear suspension systems. Furthermore, the rigid-body model predicts a better vehicle body stability following high-speed turns than the compliance model.

1 Introduction

The chassis is the backbone of any vehicle and serves as the main mounting point for all of the major components, including the engine, axles, wheels, suspension units, electrical harness, body, and so on. As the vehicle travels over the ground, the chassis transmits the ground force through the tires to the suspension system. The transmitted force causes the suspension linkages to undergo geometric deformation, and therefore changes the load taken by each hardpoint. As a consequence, the handling performance of the entire vehicle is also critically affected. To ensure a satisfactory ride quality, the relationships between the transmitted force, suspension deformation, and vehicle kinematics must be properly understood. However, it is difficult to measure the chassis kinematics directly when the vehicle is running. The suspension is an assembly of linkages which are subjected to deformation under load. Simulation during the design process shows the geometric changes to the mechanism and their effect on suspension design values, which in turn affects the load taken by each joint and the hardpoints. It is important to understand how forces act on the suspension to make specific adjustments to the linkages and the joints under uneven load and verify the deformation of each member when the whole vehicle is running and their effect on the original suspension kinematic parameters.

The geometry changes and loads to which a vehicle suspension are exposed during running are usually evaluated by Kinematics and Compliance (K&C) testing. Holdmann et al. (1998) developed a K&C test rig that used 12 sets of hydraulic actuators to control the longitudinal, lateral and vertical loads acting on each wheel in order to evaluate the suspension displacement and suspension side load. Morse (2004) proposed several practical methods for using K&C measurements to perform chassis tuning and development. Mitchell et al. (2008) compared the theoretical results obtained for the kinematic movement of a car suspension system with the results obtained from K&C testing and found a good qualitative agreement between them.

The rapid development of Computer-Aided Engineering (CAE) software in the automotive industry has dramatically shortened the development cycle and reduced costs. Li et al. (2007) proposed a method for optimizing the handling performance of a vehicle by tuning the suspension design parameters, steering system design parameters, and operating parameters. Notably, the suspension design parameters included both the kinematic parameters (e.g., the coordinates of the hardpoints in the front and rear suspensions) and the compliance parameters (e.g., the stiffness values of the springs). Analyses were conducted on the assumption that each moving part is a rigid body totally free from deformation. However, in real vehicle kinematics, each moving part is subject to partial deformation under load, and this affects vehicle performance. It was shown that combining the compliance and rigid properties of the suspension components allowed the analyses to approach the real vehicle condition more closely and improved the handling performance as a result. Huang and Lin (2017) constructed a Strut-SLA front suspension model and then applied the Taguchi method to examine the effects of different levels of flexibility in the suspension parts on the suspension performance parameters and suspension loading conditions. Krishna et al. (2000) examined the effects of compliance on the suspension forces experienced by a vehicle using a Finite Element (FE) model constructed using flexible elements. Comparing the results with those obtained using a rigid-body model, it was found that the flexibility of the suspension components resulted in a local effect, but had no significant global effect. Using dynamic testing, Yi (2000) constructed three vehicle models, namely a FE model based on nodal coordinates, a FE model based on modal coordinates, and a rigid-body model. The modeling results obtained for sinusoidal depression loads and pulse steering operations showed that a significantly different system response was obtained when the dynamic effects of chassis flexibility were taken into account.

In general, the results presented in the studies above confirm the importance of considering the flexibility of the suspension components when examining the kinematic response and handling performance of a vehicle. Accordingly, the present study constructs CAE models of the front and rear suspension units of a light-weight electric vehicle (EV) based on a double-A type design and trailing arm design, respectively. The validity of the CAE models is confirmed by comparing the results obtained for the camber angle and toe-in angle with those obtained mathematically. Quarter-vehicle simulations are then performed to compare the effects of the rigid-body and compliance assumptions, respectively, on the forces produced at the hardpoints of the two suspension systems under pothole impact loads. Finally, Quarter-vehicle simulations are conducted to evaluate the vehicle handling performance in impulse steering tests conducted using the rigid-body model and compliance model, respectively. Overall, the simulation results confirm that the choice of suspension model (i.e., compliance or rigid-body) has a significant effect on the simulation outcomes for the suspension kinematics and vehicle handling performance.

2 Design procedure

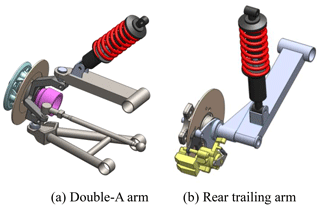
As for all passenger vehicles, two of the main considerations for the EV considered in the present study are agile handling and passenger comfort. Accordingly, as described above, the EV adopts a double-A arm type configuration for the front suspension in order to provide a good turning performance and enhanced road surface adherence (see Fig. 1a), and a trailing arm type configuration for the rear suspension to provide good passenger comfort and more rear axle space (see Fig. 1b).

Figure 1 Front and rear suspension systems in target EV.

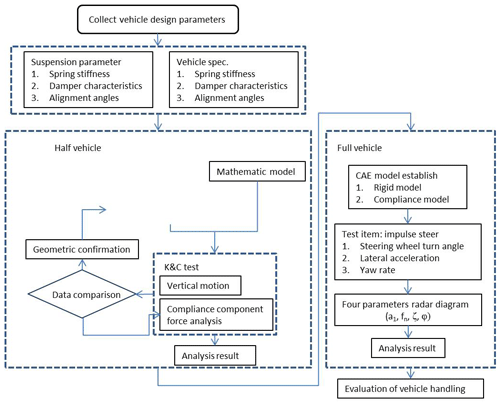
Figure 2 shows the research framework employed in the present study. The study commenced by collecting all the vehicle design parameters of interest, including the mass distribution, the position of the center of gravity, the spring stiffness, the damper characteristics, the alignment angles of the suspension components, and so on. The parameters were used to construct CAE models of the front and rear suspension units, respectively. The models were verified mathematically using the vector loop method and the linkages in the front and rear suspensions were then meshed to facilitate CAE analyses of the suspension kinematics using a Quarter-vehicle model. For comparison purposes, the forces acting at the hardpoints of the two suspension systems were evaluated using both a compliance suspension model and a rigid-body model. Finally, full-vehicle simulations were performed using both models of the suspension linkages to evaluate the kinematics and handling performance of the vehicle in impulse steering tests.

Figure 2 Research framework.

3 Vehicle specification

For a light electric vehicle, the mass should be less than 350 kg (excluding battery mass) and the maximum speed should be no greater than 45 km h⁻¹. The dimensions of the vehicle body ($L\times W\times H$) is limited to $\mathrm{4000}\times \mathrm{2000}\times \mathrm{2500}$ (mm). According to the total mass of the target vehicle comprised the mass of the suspension system (i.e., the front and rear suspension units and brakes), the power system (i.e., the motor, battery, transmission, transmission shaft, and driver), the steering system (i.e., the steering box, steering wheel, and steering column) and the body structure (including the seats). Table 1 shows the mass values of the main EV system components that fit the requirement of the light electric vehicle.

Table 1 Measured mass values of main EV system components.

The x and y coordinates of the center of gravity (CG) of the EV were determined using Eqs. (1) and (2) below with the vehicle placed on level ground. Note that the origin of the coordinate frame was located at the midpoint position of an imaginary line drawn between the centers of the two front wheels. Substituting the mass of the vehicle, together with that of the front and rear axles, into Eqs. (1) and (2), the x and y coordinates of the COG were determined to be 831.45 and 623.72 mm, respectively. Furthermore, raising the rear wheels of the EV off the ground such that the vehicle was tilted at an angle of 15^∘ to the horizontal, the y coordinate value of the COG of the EV was found from Eq. (3) to be 217.6 mm.

$$\begin{array}{}\text{(1)}& {\displaystyle }{X}_{\mathrm{CG}}={\displaystyle \frac{M_{\mathrm{r}}\times l}{M_{\mathrm{v}}}}={\displaystyle \frac{\left(\mathrm{142.6}\times \mathrm{2590}\right)}{\mathrm{444.2}}}=\mathrm{831.45},\text{(2)}& {\displaystyle }{Y}_{\mathrm{CG}}={\displaystyle \frac{(M_{\mathrm{fr}}+M_{\mathrm{rr}})\times w}{M_{\mathrm{v}}}}={\displaystyle \frac{\mathrm{234}\times \mathrm{1184}}{\mathrm{444.2}}}=\mathrm{623.72}\text{(3)}& {\displaystyle }{Z}_{\mathrm{CG}}={\displaystyle \frac{l}{M_{\mathrm{v}}}}\times {\displaystyle \frac{M_{\mathrm{\Delta }}}{\tan \mathit{\alpha }}}={\displaystyle \frac{\mathrm{2590}}{\mathrm{444.2}}}\times {\displaystyle \frac{\mathrm{10}}{\tan \mathrm{15}{}^{\circ }}}=\mathrm{217.6}\end{array}$$

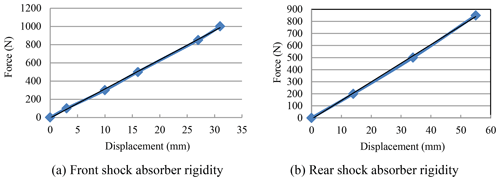
The stiffness values of the front and rear shock absorbers were determined by measuring the spring displacement under applied loads ranging from 0–1000 kg. The corresponding results are presented in Fig. 3a and b, respectively. From inspection, the stiffness of the front shock was determined to be 32 N mm⁻¹, while that of the rear shock was 15.44 N mm⁻¹.

Table 2 Basic parameters of EV.

Figure 3 Rigidity curves for front and rear shock absorbers in EV.

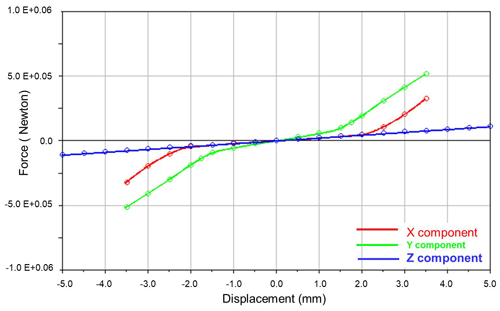
The bushing is an indispensable part of any vehicle suspension system, and serves to reduce noise, transmit direction forces and torque, and isolate the members from direct impact. The bushings used in the present EV consisted of a steel sleeve encased in rubber and placed around a central shaft. Figure 4 shows the corresponding measured force-displacement relationship.

Figure 4 Bushing characteristic curve.

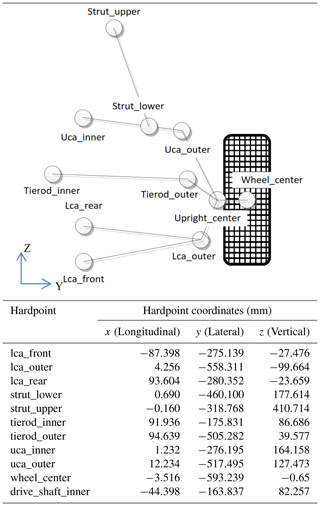
In a vehicle suspension system, the hardpoints are the non-adjustable joints or mounting points in the system and have a critical effect on the kinematics of the structure in response to the application of an external horizontal or vertical load. Table 3 shows the main hardpoints in the left front suspension of the present EV.

Table 3 Hardpoint coordinates of left front suspension.

Figure 5 Compliance model processing flowchart.

4 Construction and validation of CAE models

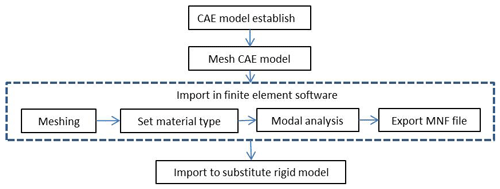
Finite element analysis software was used in this study and analyzed data was imported into the simulation software for preparation of the model. As described in Sect. 2, two models were constructed for each suspension (front and rear), namely a compliance model and a rigid-body model. The main steps in the CAE modeling process for the compliant suspension model are shown in Fig. 5 below and are summarized as follows:

Import model. The CAE model was constructed and imported into FE software.

Selection of element type. The model was implemented using eight-node elements; with each node having three DOF (see Table 4).

Meshing. The model was discretized in accordance with the meshing scheme shown in Table 4.

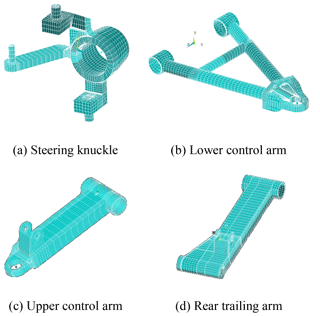
Set material properties. Appropriate values of the Poisson's ratio, elastic modulus and material density were assigned to the four compliant members of the suspension systems, namely the upper control arm, the lower control arm and the steering knuckle in the front suspension and the trailing arm in the rear suspension (see Table 4).

Modal analysis. A modal analysis was performed to determine the modal vibration type and natural frequency of the structure.

Export MNF file. The modal neutral file (MNF) was exported in the file type required by the simulation software of compliance body.

Table 4 Model construction details and material parameters for compliant members of front and rear suspensions.

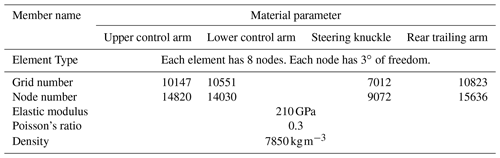
Figure 6 shows the meshed models of the upper control arm, lower control arm, steering knuckle and rear trailing arm, respectively.

Figure 6 Meshed models of compliant members of front and rear suspensions.

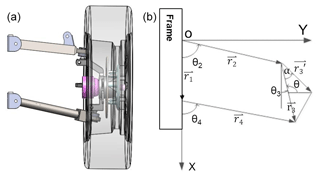
A mathematical model of the front double-A arm suspension system was constructed by calculating the angle of each linkage and the displacement of each joint using the vector loop method. The double-A arm suspension system acts independently within the chassis system such that the right tire is unaffected by bouncing of the left tire, and vice versa. Therefore, in constructing the mathematical model, a 1∕4 vehicle model was deemed to be sufficient, as shown in Fig. 7a. The vector loop method was used to analyze the mechanical positions of the front suspension members and to determine the trend of the camber and toe-in angles for various displacements of the wheel in the vertical direction. The main steps in the mathematical modeling procedure were as follows:

1. Set Point O as the origin of the coordinate frame (see Fig. 7b). The positive values of the y axis were thus equivalent to those of the inverse rotation of the x axis.

2. The vector for each linkage was expressed as r₁, r₂, r₃ and r₄ as shown in Fig. 7b. The vector loop equation was thus given as

   $$\begin{array}{}\text{(4)}& -{\mathit{r}}_{\mathrm{1}}+{\mathit{r}}_{\mathrm{2}}+{\mathit{r}}_{\mathrm{3}}-{\mathit{r}}_{\mathrm{4}}=\mathrm{0}.\end{array}$$

3. Equation (4) was resolved in the x and y directions respectively as

   $$\begin{array}{}\text{(5)}& {\displaystyle }-r_{\mathrm{1}}+r_{\mathrm{2}}\cos {\mathit{\theta }}_{\mathrm{2}}+r_{\mathrm{3}}\cos {\mathit{\theta }}_{\mathrm{3}}-r_{\mathrm{4}}\cos {\mathit{\theta }}_{\mathrm{4}}=\mathrm{0},\text{(6)}& {\displaystyle }{r}_{\mathrm{2}}\sin {\mathit{\theta }}_{\mathrm{2}}+r_{\mathrm{3}}\sin {\mathit{\theta }}_{\mathrm{3}}-r_{\mathrm{4}}\sin {\mathit{\theta }}_{\mathrm{4}}=\mathrm{0}.\end{array}$$

   Simplifying Eqs. (5) and (6) yields

   $$\begin{array}{}\text{(7)}& A\cos {\mathit{\theta }}_{\mathrm{4}}+B\sin {\mathit{\theta }}_{\mathrm{4}}=C\end{array}$$

   where $A=\mathrm{2}{r}_{\mathrm{4}}(r_{\mathrm{1}}-r_{\mathrm{2}}\cos {\mathit{\theta }}_{\mathrm{2}})$, $B=-\mathrm{2}{r}_{\mathrm{2}}{r}_{\mathrm{4}}\sin {\mathit{\theta }}_{\mathrm{2}}$, $C=(r_{\mathrm{3}}^{\mathrm{2}}-r_{\mathrm{4}}^{\mathrm{2}}-r_{\mathrm{1}}^{\mathrm{2}}-r_{\mathrm{2}}^{\mathrm{2}})+\mathrm{2}{r}_{\mathrm{1}}{r}_{\mathrm{2}}\cos {\mathit{\theta }}_{\mathrm{2}}$.

4. Substituting the known values of r₁, r₂, r₃ and r₄ into Eq. (7) together with θ₂ gives θ₄ as

   $${\mathit{\theta }}_{\mathrm{4}}=\mathit{\phi }\pm \cos \left({\displaystyle \frac{C}{\sqrt{A_{\mathrm{2}}+B_{\mathrm{2}}}}}\right),$$

   where $\mathit{\phi }={\cos }^{-\mathrm{1}}\frac{A}{\sqrt{A_{\mathrm{2}}+B_{\mathrm{2}}}}$.

5. Substituting θ₄ into Eqs. (5) and (6) gives θ₃ as

   $${\mathit{\theta }}_{\mathrm{3}}={\tan }^{-\mathrm{1}}\left({\displaystyle \frac{r_{\mathrm{4}}\sin {\mathit{\theta }}_{\mathrm{4}}-r_{\mathrm{2}}\sin {\mathit{\theta }}_{\mathrm{2}}}{r_{\mathrm{1}}+r_{\mathrm{4}}\cos {\mathit{\theta }}_{\mathrm{4}}-r_{\mathrm{2}}\cos {\mathit{\theta }}_{\mathrm{2}}}}\right).$$

   Note that θ₃ is the kingpin inclination(KPI), i.e. $\mathrm{camber}=\mathit{\theta }-\mathrm{90}-{\mathit{\theta }}_{\mathrm{3}}$

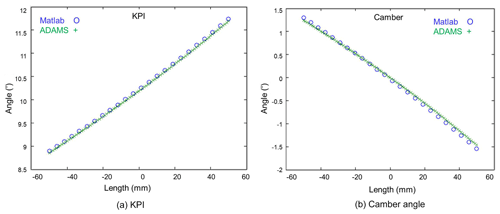
Figure 8a and b compare the ADAMS simulation results for the variations of the KPI and camber angle with the tire displacement, respectively, with the mathematical results obtained from the vector loop method.

Figure 7 1∕4 vehicle CAD model (a) and corresponding vector loop diagram (b).

Figure 8 Comparison of simulation and mathematical results with tire displacement.

A close inspection of the two figures shows that the simulation results for the toe-in angle deviate from the mathematical solutions by just 0.3 %, while the results for the camber angle vary from the mathematical solutions by no more than 4.2 %. In other words, the validity of the CAD suspension model is confirmed.

5 Force analysis

The validated 1∕4 vehicle models were used in a series of simulations to investigate the forces acting on the hardpoints of the two suspension systems under realistic road impact conditions. For comparison purposes, the forces were computed using both the compliance model and the rigid-body model.

5.1 Boundary condition settings

Table 5 (left column) shows five typical load conditions considered in the development of a vehicle suspension system. For each condition, the applied load can be resolved in three directions , namely longitudinal, lateral and vertical, where the dynamic load coefficients for the three directions are shown in the second, third and fourth columns, respectively. The present study focused on the first loading condition, namely that of the wheel falling into a pothole. Based on the measured mass values of the front and rear single wheels, the longitudinal and vertical forces acting on the two wheels were computed as follows:

Front suspension vertical load. F_Y= front single wheel mass $\times \mathrm{4}=\mathrm{4939.2}$ N,

Front longitudinal load. F_x= front single wheel mass $\times \mathrm{3}=\mathrm{3704.4}$ N,

Rear suspension vertical load. F_z= rear single wheel mass $\times \mathrm{4}=\mathrm{2234.4}$ N,

Rear suspension longitudinal load. F_x= rear single wheel mass $\times \mathrm{3}=\mathrm{1675.8}$ N.

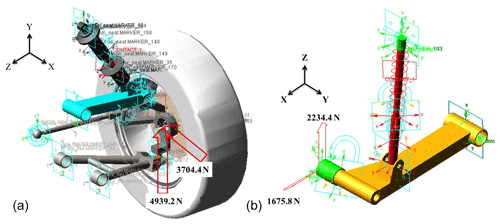
The calculated forces were applied as boundary conditions for the corresponding CAE models, as shown in Fig. 9a and b, respectively. Simulations were then performed to determine the forces acting at each of the hardpoints in the two suspension systems (see Fig. 10a and b).

Table 5 Dynamic load coefficients (Happian-Smith, 2008). Front single wheel mass: 126 kg, rear single wheel mass: 57 kg.

Figure 9 Mechanical kinematics models of: (a) front suspension, and (b) rear suspension.

5.2 Simulation results

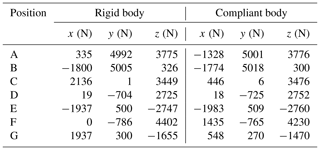
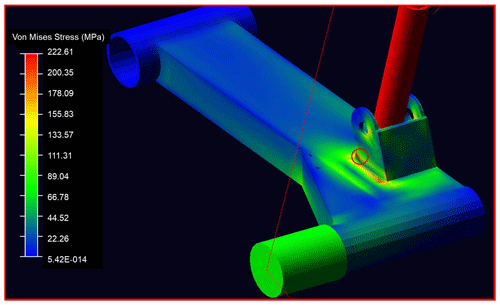
The simulation results obtained for the force distributions at the hardpoints in the front and rear suspension systems are shown in Tables 6 and 7, respectively. Note that results are presented for both the compliance model and the rigid-body model. Observing the results presented in Table 6 for the upper control arm, it is seen that the greatest difference between the results obtained using the two models occurs in the x direction at Points A and C. In the rigid-body model, the suspension members do not deform under load. Hence, the revolute joint at Point C produces a reaction force of 2136 N to counteract the displacement in the x direction. By contrast, in the compliance model, the reaction force is reduced to just 446 N since the control arm deforms under the effects of the applied load. However, the deformation of the control arm leads to a high reaction force of 1328 N at Point A, whereas the reaction force in the rigid-body model is equal to just 335 N. For the lower control arm, the maximum difference in the force results obtained from the two models occurs in the x direction at Points F and G. Point G represents the revolute joint on the inner side of the control arm. In the rigid-body model, the control arm undergoes no deformation under load, and hence all of the longitudinal force developed at Point E is borne at Point G. As a result, Point G has a high load of 1937 N in the x direction, while Point F has no load. By contrast, in the compliance model, a force of 1435 N is developed at Point F due to the linkage deformation required to counteract the force acting at Point G. For the rear suspension, the trailing arm bounces vertically under the effects of the vertical and longitudinal loads. As a result, no force components are produced in the lateral direction at any of the hardpoints in the rigid-body model (see Table 7). However, in the compliance model, a stress of 222.61 MPa is induced at the lower hardpoint of the shock absorber, as shown in Fig. 11. As a result, a side force of 1991 N is produced at both fulcrum points of the suspension system (see Table 7).

Figure 10 Force analysis at hardpoints in: (a) front suspension and (b) rear suspension.

Table 6 Forces acting at hardpoints in front suspension system in rigid-body and compliance models.

Table 7 Forces acting at hardpoints in rear suspension system in rigid-body and compliance models.

Figure 11 Trailing arm stress distribution contours.

6 Dynamic simulations

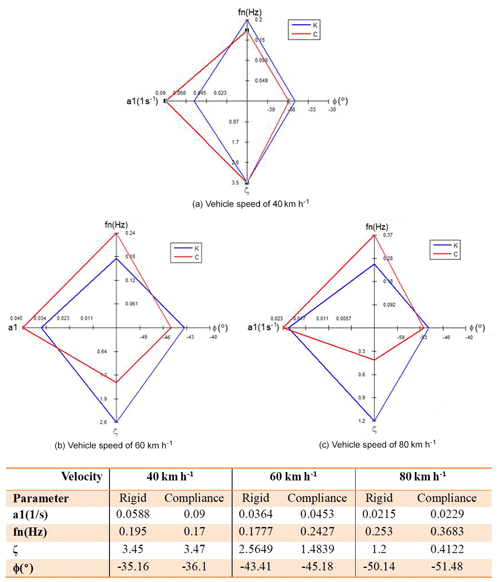
When the front and rear suspensions are subjected to forces from different directions, flexibility of the linkages changes the suspension parameters and the forces acting at the joints. Consequently, the dynamic parameters of the entire vehicle are also affected. In the present study, the dynamic behavior of the EV was investigated by means of simulated impulse steering tests; with the results represented diagrammatically in the form of four-parameter radar plots (Mimuro et al., 1990).

6.1 Impulse steering test

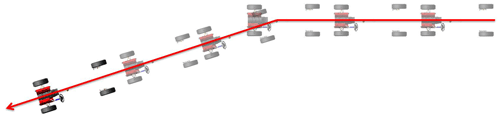
The main use of impulse steering in practical situations is to avoid an object that suddenly appears in the vehicle path while traveling at normal driving speeds. The steering characteristics of the vehicle after impulse steering provide a useful evaluation of the vehicle handling performance in terms of both the response speed and the stability. In performing an impulse steering test, the vehicle is steered at a certain angle when traveling at 70 % of its maximum speed and, when the vehicle reaches a lateral acceleration rate of 4 m s⁻², the steering wheel is returned abruptly (within 0.5 s) to the origin. The corresponding vehicle trajectory is shown in Fig. 12. The speed, steering turn angle, yaw rate and lateral acceleration rate are recorded continuously throughout the test and are then used to evaluate the handling performance.

Figure 12 Schematic illustration of impulse steering test travel route.

6.2 Two-wheel simplified model

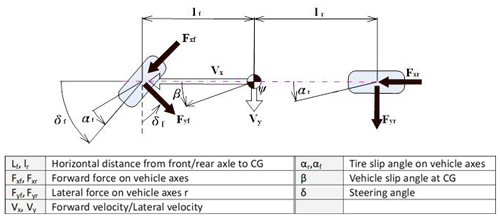
Under normal driving conditions, when a slight turn is made, the lateral acceleration rate response of the vehicle increases initially and then reduces in a linear way. However, in the impulse steering test condition, the vehicle reaches a side acceleration rate of 0.4 g under constant speed. The lateral motion of the whole vehicle therefore remains entirely within the linear range and thus a simplified two-wheel model can be used to investigate the dynamic steering behavior of the vehicle, as shown in Fig. 13.

Figure 13 Simplified two-wheel steering model.

Based on the simplified steering model, the dynamic behavior of the whole vehicle can be expressed as

$$\begin{array}{}\text{(8)}& {\displaystyle }m\left(\dot{V_x}-V_y{\mathit{\psi }}_z\right)=F_{x\mathrm{f}}\cos {\mathit{\delta }}_{\mathrm{f}}+F_{x\mathrm{r}}{F}_{y\mathrm{f}}\sin {\mathit{\delta }}_{\mathrm{f}},\text{(9)}& {\displaystyle }m\left(\dot{V_y}-V_x{\mathit{\psi }}_z\right)=F_{y\mathrm{f}}\cos {\mathit{\delta }}_{\mathrm{f}}+F_{y\mathrm{r}}+F_{x\mathrm{f}}\sin {\mathit{\delta }}_{\mathrm{f}},\text{(10)}& {\displaystyle }{I}_z\dot{{\mathit{\psi }}_z}=l_{\mathrm{f}}{F}_{y\mathrm{f}}\cos {\mathit{\delta }}_{\mathrm{f}}{l}_{\mathrm{r}}{F}_{y\mathrm{r}}+l_{\mathrm{f}}{F}_{x\mathrm{f}}\sin {\mathit{\delta }}_{\mathrm{f}}.\end{array}$$

For simplicity, the following assumptions are introduced: (1) the longitudinal acceleration rate of the vehicle is equal to zero $(\dot{V_x}=\mathrm{0})$, and hence the wheel longitudinal force is also equal to zero (F_xf=0); and (2) the wheel turn angle (δ_f) is very small, and therefore cos δ_f=1.

Given these assumptions, Eqs. (8)–(10) can be simplified as

$$\begin{array}{}\text{(11)}& {\displaystyle }m\left(\dot{V_y}-V_x{\mathit{\psi }}_z\right)=F_{y\mathrm{f}}+F_{y\mathrm{r}},\text{(12)}& {\displaystyle }{I}_z\dot{{\mathit{\psi }}_z}=l_{\mathrm{f}}{F}_{y\mathrm{f}}{l}_{\mathrm{r}}{F}_{y\mathrm{r}}.\end{array}$$

Let the stiffnesses of the front and rear tires be denoted as K_f and K_r, respectively. The lateral force acting on the vehicle can then be expressed as

$$\begin{array}{}\text{(13)}& F_{y\mathrm{f}}=\mathrm{2}{K}_{\mathrm{f}}{\mathit{\alpha }}_{\mathrm{f}},F_{y\mathrm{r}}=\mathrm{2}{K}_{\mathrm{r}}{\mathit{\alpha }}_{\mathrm{r}},\end{array}$$

where α_f and α_r are the sideslip angles of the front and rear wheels, respectively, and are given by

$$\begin{array}{}\text{(14)}& {\mathit{\alpha }}_{\mathrm{f}}={\mathit{\delta }}_{\mathrm{f}}-\mathit{\beta }-{\displaystyle \frac{l_{\mathrm{f}}\times \dot{{\mathit{\psi }}_z}}{V}}\text{ and }{\mathit{\alpha }}_{\mathrm{r}}={\mathit{\delta }}_{\mathrm{r}}-\mathit{\beta }+{\displaystyle \frac{l_{\mathrm{r}}\times \dot{{\mathit{\psi }}_z}}{V}}.\end{array}$$

Combining Eqs. (11)–(14), the simplified two-wheel steering model can be expressed in the following dynamic matrix form:

$$\begin{array}{}\text{(15)}& \begin{array}{rl}& \left[\begin{array}{ll}m{V}_x+\frac{\mathrm{2}\left(l_{\mathrm{f}}{K}_{\mathrm{f}}-l_{\mathrm{r}}{K}_{\mathrm{r}}\right)}{V}& m{V}_x\times s+\mathrm{2}\left(K_{\mathrm{f}}+K_{\mathrm{r}}\right)\\ I_z\times s+\frac{\mathrm{2}\left(l_{\mathrm{f}}^{\mathrm{2}}{K}_{\mathrm{f}}-l_{\mathrm{r}}^{\mathrm{2}}{K}_{\mathrm{r}}\right)}{V}& \mathrm{2}\left(l_{\mathrm{f}}{K}_{\mathrm{f}}-l_{\mathrm{r}}{K}_{\mathrm{r}}\right)\end{array}\right]\left[\begin{array}{c}{\mathit{\psi }}_z\\ \mathit{\beta }\end{array}\right]\\ & ={\displaystyle \frac{\mathrm{2}}{i_s}}\left[\begin{array}{c}{K}_{\mathrm{f}}\\ l_{\mathrm{f}}{K}_{\mathrm{f}}\end{array}\right]\times {\mathit{\delta }}_H\end{array}\end{array}$$

From Eq. (15), the yaw angle gain (G_yaw) and lateral acceleration rate gain (G_acc) can be further derived as

$$\begin{array}{}\text{(16)}& {\displaystyle }{G}_{\mathrm{yaw}}={\displaystyle \frac{{\mathit{\psi }}_z}{{\mathit{\delta }}_H}}={\displaystyle \frac{a_{\mathrm{1}}(\mathrm{1}+T_{\mathrm{f}}s)}{\mathrm{1}+\frac{\mathrm{2}s\mathit{\zeta }}{{\mathit{\omega }}_{\mathrm{n}}}+s^{\mathrm{2}}{\mathit{\omega }}_{\mathrm{n}}^{\mathrm{2}}}},\text{(17)}& {\displaystyle }{G}_{\mathrm{acc}}={\displaystyle \frac{a_y}{{\mathit{\delta }}_H}}={\displaystyle \frac{a_{\mathrm{3}}(\mathrm{1}+b_{\mathrm{1}}s+b_{\mathrm{2}}{s}^{\mathrm{2}})}{\mathrm{1}+\frac{\mathrm{2}s\mathit{\zeta }}{{\mathit{\omega }}_{\mathrm{n}}}+s^{\mathrm{2}}{\mathit{\omega }}_{\mathrm{n}}^{\mathrm{2}}}}\end{array}$$

where s: Laplace transform operator, ψ: Yaw rate, a_y: Lateral acceleration rate, β: Angle of sideslip, I_z: Vehicle moment of inertia in z direction, δ_H: Steering wheel turn angle, ω_n: Natural frequency, ζ: System damping ratio, T_f: System constant.

6.3 Objective evaluation

In the present study, the simulation results obtained for the vehicle handling performance were visualized using radar diagrams constructed using four parameters, namely:

• The yaw rate gain (plotted along the left axis a₁). The yaw rate gain produced at each turn angle of the steering wheel represents the ease (or otherwise) of steering the corresponding heading. If the yaw rate gain is too small, the steering response will be sluggish and slow. Consequently, a better (i.e., more agile and responsive) handling performance is indicated by a higher (more leftward) value of the yaw rate gain in the radar plot.

• The steering heading (plotted along the upper vertical axis f_n). The steering heading represents the responsiveness of a particular steering heading and is quantified as the relationship between the steering wheel turn angle and the yaw rate. A better handling performance is indicated by a higher steering heading, which implies a shorter yaw rate response time.

• The directional damping (plotted along the lower vertical axis ζ). The directional damping is defined as the ratio of the steady yaw rate gain to the transient yaw rate gain. In general, the inhibition of the vehicle heading to sway deteriorates as the value of the directional damping reduces. When the vehicle speed is low, the damping effect is small and can be effectively ignored. However, as the vehicle speed rises, the damping effect becomes small, and thus the stability of the vehicle deteriorates. In other words, a better handling performance is indicated by a higher directional damping value.

• The controllability (plotted along the right axis ψ). The controllability is defined as the phase lag angle when the lateral acceleration rate has a 1 Hz frequency response. In general, a longer phase delay indicates a slower response of the vehicle to the lateral acceleration rate and steering wheel turn angle. By contrast, a smaller value indicates that the lateral acceleration rate reaches its peak value more rapidly. In other words, an improved drivability is achieved. Thus, a better handling performance is indicated by a smaller (more rightward) value of the controllability in the radar plot.

Based on the discussions above, it is clear that a greater diamond area of the radar plot represents a better handling performance. However, it should be noted that the four parameters used to construct the plot are mutually interactive. That is, an excessive value of one of the parameters may lead to a reduction in the effects of the other parameters.

In the present study, the impulse steering test was simulated for three different vehicle speeds, namely 40, 60 and 80 km h⁻¹, respectively. For each simulation, the steering wheel angle, yaw rate and lateral acceleration rate were obtained in the time domain and then converted into frequency-domain values using fast Fourier transformation. The transfer functions of the yaw rate gain and lateral acceleration rate gain, respectively, were acquired via data reconstruction and the system identification method. Finally, the transfer functions were used to determine the four parameters required to construct the radar diagrams. The simulations were performed using both the rigid-body suspension model and the compliance model. The results are presented in Fig. 14 for vehicle speeds of 40, 60 and 80 km h⁻¹, respectively.

Figure 14 Radar plots for different velocity.

Observing the three tables, it is clear that a significant difference exists in the handling performance of the vehicle when evaluated using the rigid-body model and compliance model, respectively. For example, for each of the vehicle speeds, the yaw rate gain computed using the compliance model is greater than that computed using the rigid-body model. For a low travel speed of 40 km h⁻¹, the steering heading calculated using the rigid-body model is higher than that calculated using the compliance model. However, at higher speeds of 60 and 80 km h⁻¹, a reverse tendency is observed. For higher values of the steering heading, the vehicle yaw rate response time to the steering wheel rotation decreases. In other words, the handling performance improves. For vehicle speeds of 60 and 80 km h⁻¹, the directional steering damping (ζ) computed using the rigid-body model is notably larger than that computed using the compliance model. In other words, the stability of the vehicle body following impulse steering is improved compared to that predicted by the compliance model. Finally, for all vehicle speeds, the controllability computed using the rigid-body model is smaller than that computed using the compliance model. In other words, the rigid-body model predicts a better vehicle handling performance (i.e., a faster vehicle lateral acceleration rate response in a turn) than the compliance model.

7 Conclusions

This study has conducted FE simulations to compare the suspension kinematics and handling performance of a lightweight EV when modeling the front and rear suspension systems using either a rigid-body model or a compliance model, respectively. The simulations have commenced by examining the forces acting at the hardpoints of the two suspension systems under a typical pothole impact loading condition. The effects of the linkage deformation behavior (i.e., rigid-body or compliant) on the handling performance of the EV have then been investigated by means of simulated impulse steering tests performed at vehicle speeds in the range of 40–80 km h⁻¹. The results of the impulse steering simulations have been visualized using radar plots based on four parameters, namely the yaw rate gain, the steering heading, the directional steering damping and the controllability. Overall, the simulation results obtained in the present study support the following main conclusions.

The validity of the CAE suspension models has been confirmed by comparing the simulation results obtained for the camber angle and toe-in angle with those obtained mathematically using the vector loop method. It has been shown that the analytical solutions deviate from the mathematical solutions by no more than 4.2 %.

For pothole impact loads, the forces computed at some of the hardpoints in the front and rear suspension systems vary significantly depending on whether a rigid-body model or a compliance model is employed. For example, in the front suspension system, the rigid-body model predicts a force of 2136 N at the end of the upper control arm, whereas the compliance model predicts a value of just 446 N. By contrast, in the rear suspension system, the rigid-body model indicates the absence of any lateral forces at the hardpoints, whereas the compliance model predicts a maximum lateral force of 1991 N.

In the impulse steering tests, the simulation outcomes for the vehicle handling performance depend on the choice of suspension model (i.e., rigid-body or compliance). For example, the compliance model predicts a better yaw rate response of the vehicle at all of the considered vehicle speeds, whereas the rigid-body model predicts an improved vehicle body stability.