Study on the tooth surface wear characteristics of helical gears under mixed elastohydrodynamic lubrication

Existing research on tooth surface wear of helical gears has insufficiently considered the complex and variable lubrication conditions between meshing tooth surfaces. This study constructed a mixed elastohydrodynamic lubrication (EHL) model based on the meshing characteristics of helical gears, analyzed the lubrication characteristics between the meshing tooth surfaces and the temperature changes induced by asperity contact and oil film shear, and introduced them into the improved Archard wear model to construct the surface wear calculation model under the mixed EHL conditions. Taking the changes in meshing characteristics of tooth profile during the tooth surface wear accumulation process as a connecting bridge, the mutual influence relationships among the tooth surface wear, lubrication characteristics, and tooth surface temperature rise were systematically clarified. The cumulative distribution law of tooth surface wear and the influence of tooth surface roughness, working conditions, and tooth profile parameters on the tooth surface wear depth were explored. The research indicates that the wear depth at the tooth root and top is deeper than that at the pitch position, the pinion's surface wear depth is greater than that of the gear, and the maximum wear appears at the pinion's tooth root. The wear depth under mixed EHL conditions is nearly 4 orders of magnitude lower than that under dry friction conditions. Reducing the magnitude of tooth surface roughness can effectively decrease the tooth surface wear depth. Appropriately increasing the velocity, module, tooth width, helix angle and tooth surface hardness is beneficial to improving the anti-wear ability of tooth surfaces. This study can provide a reliable theoretical basis for predicting and optimizing the tooth surface wear of helical gears under complex lubrication conditions.

1 Introduction

Helical gears are widely used in all kinds of mechanical equipment owing to their advantages of smooth transmission, large contact ratio, and strong load carrying capacity. During the operation of gears, motion and power are mainly transferred via the meshing tooth surfaces. Owing to factors like inadequate lubrication, overloaded operation, and tooth surface defects, tooth surface wear has emerged as one of the more prevalent failure modes in gear transmission systems. During the entire service life of a gear drive, the inescapable relative sliding between meshing tooth surfaces leads to tooth surface wear, which is an inevitable consequence of the frictional forces acting on the tooth surfaces (Zhou et al., 2018). Tooth wear leads to progressive degradation of the gear mesh interface. Severe tooth surface wear can cause the gear tooth thickness to decrease, trigger vibration and noise, lower the gear transmission efficiency and smoothness, and potentially induce or hasten gear failure (Wang, 2017; Jia et al., 2024). As the gear transmission system is developing towards the directions of high velocity, heavy load, high precision, high efficiency, and low vibration and noise, the demand for gear tooth surface wear resistance has increased dramatically. Therefore, it is highly significant to conduct research on gear tooth surface wear characteristics to slow down the tooth surface wear process, improve gear transmission performance, and increase service life and transmission efficiency.

Numerous scholars worldwide have conducted extensive research on gear tooth surface wear. The wear calculation models recognized as more authoritative and experimentally verified are mainly the Archard wear model and Bayer wear model. Among them, the Archard wear model, which takes contact stress and sliding distance between meshing tooth surfaces as the main influencing factors, is most widely used (Wang, 2016). Park and Kahraman (2009, 2012) combined the Archard wear model, the finite element method, and the semi-analytical contact model to put forward a method for calculating the tooth surface wear of hypoid gears. Flodin and Andersson (1997, 2000, 2001) proposed a point-to-point sliding distance formula based on the impact of tooth surface wear on the meshing characteristics of gears and improved the tooth surface wear calculation model of spur and helical gears, respectively. Zhang and Liu (2015) combined the finite element method and Archard wear formula to establish a tooth surface wear model of spur gears and investigated the influence of different factors on the wear depth. Zhang et al. (2017) and Zhou et al. (2021) established different tooth surface wear models of spur gears derived from the Hertz contact theory and the Archard wear formula. Wu and Cheng (1993) established a tooth face slip wear analysis model based on the equivalent contact model for spur gears and investigated the wear in the direction of the meshing line. Ding and Kahraman (2007) investigated the interactions between the tooth surface wear characteristics of gears and their dynamic response and proposed a dynamic gear tooth surface wear calculation model. Pan et al. (2012) applied the Archard wear model, fully considered the impact of gear load and velocity on the tooth surface wear of involute spur gears, and established a tooth surface wear life prediction model. Wei et al. (2023) combined the Archard wear calculation formula and Hertz contact theory to establish a wear model of VH-CATT cylindrical gears and investigated the tooth surface wear distribution under quasi-static working condition. Liu et al. (2016) and Liu (2022) proposed a dynamic tooth surface wear prediction method and investigated the coupling effect between tooth surface wear and dynamic characteristics of different gear forms. Wang et al. (2023) used Hertzian point contact simulation to solve the tooth edge contact stress concentration solution problem from the topological modification of ease-off differential surface and used the classical Archard wear model to obtain the wear depth of the contact tooth surface. Jiang et al. (2021) put forward a dynamic anti-wear modification design and analytical method, aiming to improve the dynamic performance of hypoid gears and reducing tooth surface wear. Most of the above studies on gear tooth surface wear characteristics are based on the classic Archard wear model, which is proposed according to the dry contact state, and the lubrication effect between the meshing tooth surfaces is not sufficiently considered, resulting in large inaccuracies between the calculated and actual tooth surface wear depth.

The actual tooth surface presents roughness and irregularity. The lubricant film existing between the meshing tooth surfaces in the lubrication station is comparable to the roughness by orders of magnitude, so the gear meshing interface is usually in the mixed elastohydrodynamic lubrication (EHL) state (Wu et al., 2020). In recent years, domestic and foreign scholars have successively proposed a number of improved mixed EHL solution models for gears, laying a solid foundation for the contact analysis and wear analysis of the gear interface (Ren et al., 2009; Dong et al., 2018; Wu et al., 2022). In order to accurately predict the tooth surface wear, Zhang et al. (2018) proposed an oil-lubricated spur gear tooth surface wear analysis model based on the measured tooth morphology characteristics and studied the tooth surface wear process from the microscopic scale. Akbarzadeh and Khonsari (2009) constructed a tooth surface wear prediction model based on the load sharing theory for the tooth surface wear under the mixed EHL conditions and validated the precision of the model by experiments. Masjedi and Khonsari (2012, 2015) derived the film thickness equation and the prediction formula of the asperity load ratio under mixed EHL conditions and proposed a fast method for predicting tooth surface wear. Yin and Fan (2022) established the tooth surface wear prediction model of double involute gears under the mixed EHL conditions based on its meshing characteristics and investigated the tooth surface wear depth and wear life of this type of gears. Liu et al. (2020) established a tooth surface wear model dependent on the contact pressure distribution obtained from the generalized Reynolds equation, combined with the Archard wear model and the multiaxial fatigue theory and investigated the competitive mechanism under the tooth surface wear inefficiency mode. Wang et al. (2021) put forward a method for predicting the tooth surface wear life of herringbone gears in the mixed EHL conditions. Chen et al. (2024) simulated the rough surface of a typical machined tooth profile by Fourier transform and Johnson transform and then calculated the surface wear under different machined tooth profiles. The above research on gear tooth surface wear characteristics has fully considered the effect of the lubrication state between the meshing tooth surfaces, but in the mixed EHL conditions, surface asperities and oil film shear will generate a large amount of heat, so the temperature of the tooth surfaces and the lubricating oil increases, resulting in the reduction of lubricating oil viscosity, which will affect the lubrication state. Alterations in the lubrication condition conversely influence the tooth surface wear procedure, while the tooth surface wear modifies the lubrication features between the meshing surfaces by transforming the tooth profile.

Figure 1 Contact line length in the plane of engagement: (a) ε_α≤ε_γ and (b) ε_α>ε_γ .

In summary, there is a mutual influence between gear tooth surface wear characteristics and tooth profile meshing characteristics, the lubrication state, and tooth surface temperature rise. The current research on this aspect is relatively limited, resulting in a lack of regular understanding of the gear tooth surface wear mechanism. To address this issue, this paper first adopts the segmentation method to study the meshing characteristics of helical gears and, on this basis, establishes a mixed EHL model and a tooth surface wear prediction model. By capturing the influence of tooth surface wear on the geometric parameters of gear tooth profiles, the meshing parameters of helical gears are updated in real time and fed back to the next round of lubrication analysis and tooth surface wear analysis, thus forming a real-time interaction mechanism among meshing characteristics, lubrication state, and tooth surface wear characteristics. This allows for a systematic exploration of the distribution of helical gear tooth surface wear under lubrication conditions and quantification of the impact of various parameters on tooth surface wear.

2 Meshing characteristics of helical gears

2.1 Contact line length and tooth load of helical gear

According to the relationship between the size of transverse ratio ε_α and overlap ratio ε_γ, the variation of the contact line length on the meshing plane of helical gearing can be categorized into two cases in Fig. 1.

When ε_α≤ε_γ, the ith contact line at time t is

$$\begin{array}{}\text{(1)}& l(i,t)=\left\{\begin{array}{ll}\frac{P_{\text{bt}}t}{\sin {\mathit{\beta }}_{\mathrm{b}}{T}_{\mathrm{c}}}& \mathrm{0}\le t\le {\mathit{\epsilon }}_{\mathit{\alpha }}{T}_{\mathrm{c}}\\ \frac{P_{\text{bt}}}{\sin {\mathit{\beta }}_{\mathrm{b}}}{\mathit{\epsilon }}_{\mathit{\alpha }}& {\mathit{\epsilon }}_{\mathit{\alpha }}{T}_{\mathrm{c}}<t\le {\mathit{\epsilon }}_{\mathit{\beta }}{T}_{\mathrm{c}}\\ \frac{P_{\text{bt}}}{\sin {\mathit{\beta }}_{\mathrm{b}}}\left({\mathit{\epsilon }}_{\mathit{\gamma }}-\frac{t}{T_{\mathrm{c}}}\right)& {\mathit{\epsilon }}_{\mathit{\beta }}{T}_{\mathrm{c}}<t\le {\mathit{\epsilon }}_{\mathit{\gamma }}{T}_{\mathrm{c}}\\ \mathrm{0}& {\mathit{\epsilon }}_{\mathit{\gamma }}{T}_{\mathrm{c}}\le t\le \text{ceil}\left({\mathit{\epsilon }}_{\mathit{\gamma }}\right)T_{\mathrm{c}}.\end{array}\right.\end{array}$$

When ε_α>ε_γ, the ith contact line at time t is

$$\begin{array}{}\text{(2)}& l(i,t)=\left\{\begin{array}{ll}\frac{P_{\text{bt}}t}{\sin {\mathit{\beta }}_{\mathrm{b}}{T}_{\mathrm{c}}}& \mathrm{0}\le t\le {\mathit{\epsilon }}_{\mathit{\beta }}{T}_{\mathrm{c}}\\ \frac{P_{\text{bt}}}{\sin {\mathit{\beta }}_{\mathrm{b}}}{\mathit{\epsilon }}_{\mathit{\beta }}& {\mathit{\epsilon }}_{\mathit{\beta }}{T}_{\mathrm{c}}<t\le {\mathit{\epsilon }}_{\mathit{\alpha }}{T}_{\mathrm{c}}\\ \frac{P_{\text{bt}}}{\sin {\mathit{\beta }}_{\mathrm{b}}}\left({\mathit{\epsilon }}_{\mathit{\gamma }}-\frac{t}{T_{\mathrm{c}}}\right)& {\mathit{\epsilon }}_{\mathit{\alpha }}{T}_{\mathrm{c}}<t\le {\mathit{\epsilon }}_{\mathit{\gamma }}{T}_{\mathrm{c}}\\ \mathrm{0}& {\mathit{\epsilon }}_{\mathit{\gamma }}{T}_{\mathrm{c}}\le t\le \text{ceil}\left({\mathit{\epsilon }}_{\mathit{\gamma }}\right)T_{\mathrm{c}},\end{array}\right.\end{array}$$

where T_c is the meshing period, ceil (ε_γ) is the smallest integer greater than ε_γ, and P_bt is the transverse distance.

Based on the contact line length percentage method, the load on the ith contact line at time t is

$$\begin{array}{}\text{(3)}& F(i,t)={\displaystyle \frac{l(i,t)}{L_{\mathrm{z}}\left(t\right)}}{F}_{\mathrm{z}}\left(t\right),\end{array}$$

where F_z(t) is the total load borne by all meshing tooth pairs at time t. l(i,t) is the ith contact line length at moment t. L_z(t) is the total length of all the contact lines corresponding to the meshing tooth pairs at moment t.

Figure 2 Equivalent modeling of helical gears meshing with a single pair of teeth: (a) engagement schematic and (b) segmentation model.

2.2 The motion characterization of helical gears

According to helical gears' meshing characteristics, one of its meshing transients can be equated to a pair of reversed conical roller contacts with parallel axes (Masjedi and Khonsari, 2015; Yin and Fan, 2022), as shown in Fig. 2a. During the meshing transmission of helical gears, the friction state of a specific meshing position on the tooth profile varies at different meshing moments, and the friction state also differs among different meshing positions at the same meshing moment. To accurately capture the contact states of the tooth profile at different meshing moments and positions, the idea of the segmentation method is adopted to segment the contact line (Fig. 2b), and then the comprehensive curvature radius of the ith contact line for the jth segment at point k is

$$\begin{array}{}\text{(4)}& R(i,j)={\displaystyle \frac{R_{\mathrm{1}}(i,j)R_{\mathrm{2}}(i,j)}{R_{\mathrm{1}}(i,j)+R_{\mathrm{2}}(i,j)}},\end{array}$$

where R_1,2(i,j) stands for the curvature radius of the pinion and gear tooth profiles at the meshing points, respectively.

$$\begin{array}{}\text{(5)}& \left\{\begin{array}{l}{R}_{\mathrm{1}}(i,j)=(N_{\mathrm{1}}{B}_{\mathrm{2}}+(i-\mathrm{1})L/i)/\cos {\mathit{\beta }}_{\mathrm{b}}\\ R_{\mathrm{2}}(i,j)=(N_{\mathrm{1}}{N}_{\mathrm{2}}-(N_{\mathrm{1}}{B}_{\mathrm{2}}+(i-\mathrm{1})L/i\left)\right)/\cos {\mathit{\beta }}_{\mathrm{b}},\end{array}\right.\end{array}$$

where N₁N₂ is the theoretical meshing line length.

The tangential velocities of the pinion and gear at meshing position k are

$$\begin{array}{}\text{(6)}& \left\{\begin{array}{l}{u}_{\mathrm{1}}(i,j)={\mathit{\omega }}_{\mathrm{1}}{R}_{\mathrm{1}}(i,j)\cos {\mathit{\beta }}_{\mathrm{b}}\\ u_{\mathrm{2}}(i,j)={\mathit{\omega }}_{\mathrm{2}}{R}_{\mathrm{2}}(i,j)\cos {\mathit{\beta }}_{\mathrm{b}},\end{array}\right.\end{array}$$

where ω_1,2 is the angular velocity of each of the two gears.

The relative sliding velocity u_s, entrainment velocity u_r and slide-to-roll ratio S_r at point k are

$$\begin{array}{}\text{(7)}& \left\{\begin{array}{l}{u}_{\mathrm{s}}(i,j)=\left|u_{\mathrm{1}}(i,j)-u_{\mathrm{2}}(i,j)\right|\\ u_{\mathrm{r}}(i,j)=\left[u_{\mathrm{1}}\right(i,j)+u_{\mathrm{2}}(i,j\left)\right]/\mathrm{2}\\ S_{\mathrm{r}}(i,j)=u_{\mathrm{s}}(i,j)/u_{\mathrm{r}}(i,j).\end{array}\right.\end{array}$$

According to the point-to-point sliding distance calculation method proposed by Flodin and Andersson (1997, 2000, 2001), the sliding distance at the meshing point of the pinion and gear tooth profile is denoted as

$$\begin{array}{}\text{(8)}& \left\{\begin{array}{l}{S}_{\mathrm{1}}(i,j)=\mathrm{2}b\left|u_{\mathrm{1}}(i,j)-u_{\mathrm{2}}(i,j)\right|/u_{\mathrm{1}}(i,j)\\ S_{\mathrm{2}}(i,j)=\mathrm{2}b\left|u_{\mathrm{1}}(i,j)-u_{\mathrm{2}}(i,j)\right|/u_{\mathrm{2}}(i,j),\end{array}\right.\end{array}$$

where b is the half contact width, and $b=\sqrt{\mathrm{4}wR/\left(\mathit{\pi }{E}^{\prime }\right)}$. w is the unit line load, and $w=F/l$. E^′ refers to the integrated elastic modulus, and the formula for its calculation is

$$\begin{array}{}\text{(9)}& {\displaystyle \frac{\mathrm{1}}{E^{\prime }}}={\displaystyle \frac{\mathrm{1}-{\mathit{\upsilon }}_{\mathrm{1}}^{\mathrm{2}}}{E_{\mathrm{1}}}}+{\displaystyle \frac{\mathrm{1}-{\mathit{\upsilon }}_{\mathrm{2}}^{\mathrm{2}}}{E_{\mathrm{2}}}},\end{array}$$

where υ_1,2 and E_1,2 stand for the Poisson's ratio and elastic modulus, respectively.

3 Tooth surface wear model of helical gears

3.1 The mixed EHL model of line contact

In line with the load sharing theory, the load acting on the meshing tooth surfaces under mixed EHL station is borne by the oil film and the asperities. To quickly estimate the tooth surface wear under mixed EHL conditions, this paper adopts the calculation formulas of film thickness and asperity load put forward by Masjedi et al. The central oil film thickness h_c, minimum oil film thickness h_min, asperity load ratio L_a, and film thickness ratio Λ are (Masjedi and Khonsari, 2015)

$$\begin{array}{}\text{(10)}& \left\{\begin{array}{l}{h}_{\mathrm{c}}=\mathrm{2.691}R{W}^{-\mathrm{0.135}}{U}^{\mathrm{0.705}}{G}^{\mathrm{0.556}}\\ \times (\mathrm{1}+\mathrm{0.2}{\stackrel{\mathrm{‾}}{\mathit{\sigma }}}^{\mathrm{1.222}}{\stackrel{\mathrm{‾}}{H}}^{\mathrm{0.223}}{W}^{-\mathrm{0.229}}{U}^{-\mathrm{0.748}}{G}^{-\mathrm{0.842}})\\ h_{min}=\mathrm{1.652}R{W}^{-\mathrm{0.077}}{U}^{\mathrm{0.716}}{G}^{\mathrm{0.695}}\\ \times (\mathrm{1}+\mathrm{0.026}{\stackrel{\mathrm{‾}}{\mathit{\sigma }}}^{\mathrm{1.12}}{\stackrel{\mathrm{‾}}{H}}^{\mathrm{0.185}}{W}^{-\mathrm{0.312}}{U}^{-\mathrm{0.809}}{G}^{-\mathrm{0.977}})\\ L_{\mathrm{a}}=\mathrm{0.005}{W}^{-\mathrm{0.408}}{U}^{-\mathrm{0.088}}{G}^{\mathrm{0.103}}\\ \times \ln (\mathrm{1}+\mathrm{4470}{\stackrel{\mathrm{‾}}{\mathit{\sigma }}}^{\mathrm{6.015}}{\stackrel{\mathrm{‾}}{H}}^{\mathrm{1.168}}{W}^{\mathrm{0.485}}{U}^{-\mathrm{3.741}}{G}^{-\mathrm{2.898}})\\ \mathrm{\Lambda }=h_{min}/\mathit{\sigma },\end{array}\right.\end{array}$$

where the film thickness ratio Λ serves as a significant criterion for evaluating the lubrication state between meshing tooth surfaces. When Λ≤ 0.4, the load is all borne by the asperities, and the gear pair is in dry contact conditions. When 0.4 $<\mathrm{\Lambda }\le$ 1, the load is mainly borne by the asperities, and the gear pair is in a boundary lubrication conditions. When 1 $<\mathrm{\Lambda }\le$ 3, the load is carried jointly by the asperities and the oil film, and the gear pair is in the mixed EHL state. When Λ>3, the entire load is borne by the oil film, with the gear pair being in the fluid lubrication state. W, U, $\stackrel{\mathrm{‾}}{\mathit{\sigma }}$, G, $\stackrel{\mathrm{‾}}{H}$, and σ stand for dimensionless load, velocity, tooth surface roughness, material parameter, tooth surface hardness, and dimensional tooth surface roughness. The calculation formulas are

$$\begin{array}{}\text{(11)}& \begin{array}{rl}& W=w/R{E}^{\prime },U={\mathit{\mu }}_{\mathrm{0}}{u}_{\mathrm{r}}/R{E}^{\prime },\stackrel{\mathrm{‾}}{\mathit{\sigma }}=\mathit{\sigma }/R,G=\mathit{\alpha }{E}^{\prime },\\ & \stackrel{\mathrm{‾}}{H}=H/E^{\prime },\end{array}\end{array}$$

where μ₀ is the initial lubricating oil viscosity, α is the pressure viscosity coefficient, and H is tooth hardness.

3.2 Tooth surface wear model

According to Masjedi and Khonsari's modeling of tooth surface wear under mixed EHL conditions, the gear tooth surface wear volume V_lub per unit time is (Wu et al., 2022; Liu et al., 2020)

$$\begin{array}{}\text{(12)}& V_{\text{lub}}=K\mathit{\psi }\left({\displaystyle \frac{L_{\mathrm{a}}}{\mathrm{100}}}\right){\displaystyle \frac{F{u}_{\mathrm{s}}}{H}},\end{array}$$

where ψ is the fractional film defect, and its calculation formula is

$$\begin{array}{}\text{(13)}& \mathit{\psi }=\mathrm{1}-\exp \left[-{\displaystyle \frac{X}{u_{\mathrm{s}}{t}_{\mathrm{0}}}}\exp \left(-{\displaystyle \frac{E_{\mathrm{a}}}{R_{\mathrm{g}}{T}_{\mathrm{s}}}}\right)\right],\end{array}$$

where X is the molecular diameter of the lubricant, t₀ is the basic time of molecular vibration in the adsorbed state, E_a is the heat adsorbed by the interfacial lubricant, and R_g is the molar gas constant. T_s is the interface flash temperature, and $T_{\mathrm{s}}=T_{\mathrm{0}}+\mathrm{\Delta }T$. T₀ is the bulk temperature of the gears, and ΔT is the surface temperature rise. In accordance with the flash temperature theory put forward by Tian and Kennedy, its calculation formula is (Wang et al., 2021)

$$\begin{array}{}\text{(14)}& \mathrm{\Delta }T={\displaystyle \frac{\mathrm{2}bq}{\sqrt{\mathit{\pi }}\left(K_{\mathrm{1}}\sqrt{\mathrm{1}+P_{\mathrm{e}\mathrm{1}}}+K_{\mathrm{2}}\sqrt{\mathrm{1}+P_{\mathrm{e}\mathrm{2}}}\right)}},\end{array}$$

where K_i ($i=\mathrm{1},\mathrm{2}$) is the thermal conductivity of gears. P_ei denotes the Péclet coefficients of the contact surfaces, $P_{\mathrm{e}i}=b{u}_{\mathrm{s}}/\left(\mathrm{2}{k}_i\right)$, and k_i represents the thermal diffusivity of gears. q indicates the average heat value of gears under the state of the mixed EHL, which is composed of heat q_a generated by asperities contact and heat q_h generated by oil film shear. The calculation formulas are as follows:

$$\begin{array}{}\text{(15)}& \left\{\begin{array}{l}q=q_{\mathrm{a}}+q_{\mathrm{h}}\\ q_{\mathrm{a}}=f_{\mathrm{c}}{u}_{\mathrm{s}}{p}_{\mathrm{a}}=f_{\mathrm{c}}{u}_{\mathrm{s}}p(L_{\mathrm{a}}/\mathrm{100})\\ q_{\mathrm{h}}={\mathrm{\Lambda }}_{\text{lim}}{u}_{\mathrm{s}}{p}_{\mathrm{h}}={\mathrm{\Lambda }}_{\text{lim}}{u}_{\mathrm{s}}p(\mathrm{1}-L_{\mathrm{a}}/\mathrm{100}),\end{array}\right.\end{array}$$

where f_c denotes the asperity friction coefficient. Λ_lim is the ultimate shear stress coefficient. p denotes the average contact pressure, which is composed of the oil film pressure p_h and the asperity contact pressure p_a, and their calculation formulas are

$$\begin{array}{}\text{(16)}& \left\{\begin{array}{l}p=p_{\mathrm{a}}+p_{\mathrm{h}}=\mathrm{4}F(i,t)/\mathrm{3}\mathit{\pi }bl(i,t)\\ p_{\mathrm{a}}=p(L_{\mathrm{a}}/\mathrm{100})\\ p_{\mathrm{h}}=p(\mathrm{1}-L_{\mathrm{a}}/\mathrm{100}).\end{array}\right.\end{array}$$

Both sides of Eq. (12) are simultaneously divided by the sliding velocity u_s and contact area A to obtain the gear tooth surface's wear depth per unit sliding distance:

$$\begin{array}{}\text{(17)}& {\displaystyle \frac{V_{\text{lub}}}{A{u}_{\mathrm{s}}}}=K\mathit{\psi }\left({\displaystyle \frac{L_{\mathrm{a}}}{\mathrm{100}}}\right){\displaystyle \frac{F{u}_{\mathrm{s}}}{HA{u}_{\mathrm{s}}}}\iff {\displaystyle \frac{h_{\text{lub}}}{u_{\mathrm{s}}}}=K\mathit{\psi }\left({\displaystyle \frac{L_{\mathrm{a}}}{\mathrm{100}}}\right){\displaystyle \frac{p}{H}},\end{array}$$

where wear volume V_lub=Ah_lub, and average contact pressure $p=F/A$.

Thus, in the mixed EHL conditions, the wear depth at any engagement point on the pinion and gear after a single engagement is

$$\begin{array}{}\text{(18)}& h_{\text{lub}\mathrm{1},\mathrm{2}}(i,j)={\int }_{\mathrm{0}}^{s}K\mathit{\psi }\left({\displaystyle \frac{L_{\mathrm{a}}}{\mathrm{100}}}\right){\displaystyle \frac{p(i,j)}{H}}\mathrm{d}{s}_{\mathrm{1},\mathrm{2}}(i,j).\end{array}$$

After N times of engagements, the cumulative tooth surface wear depth at the pinion and gear's engagement point is

$$\begin{array}{}\text{(19)}& \begin{array}{rl}{h}_{\text{lub}\mathrm{1},\mathrm{2}\left(N\right)}(i,j)=& h_{\text{lub}\mathrm{1},\mathrm{2}(N-\mathrm{1})}(i,j)+{\int }_{\mathrm{0}}^{s}K\mathit{\psi }\left({\displaystyle \frac{L_{\mathrm{a}}}{\mathrm{100}}}\right)\\ & \times {\displaystyle \frac{p(i,j)}{H}}\mathrm{d}{s}_{\mathrm{1},\mathrm{2}}(i,j).\end{array}\end{array}$$

Figure 3 Calculation flow chart for tooth surface wear depth of helical gears in mixed EHL conditions.

4 Tooth surface wear analysis of helical gears

The parameters of helical gears in terms of geometry, lubricant, and working conditions are presented in Table 1, and Fig. 3 presents the tooth surface wear depth calculation process of helical gears in the mixed EHL conditions. First, the segmentation method is employed to calculate the variations in meshing parameters of helical gears during the initial meshing cycle, including equivalent radius of curvature, relative sliding velocity, sliding distance, and tooth surface load. These parameters are then substituted into the mixed EHL model proposed by Masjedi et al. to obtain the variation of tooth surface contact pressure, tooth surface flash temperature, and asperity load ratio. Subsequently, these results are put into the modified Archard tooth surface wear model, yielding the tooth surface wear depth for a single meshing cycle. Based on the instantaneous tooth surface wear condition, the gear tooth profile is updated in real time to acquire the meshing characteristics of the worn tooth profile. Then, the updated meshing parameters that incorporate tooth surface wear are substituted back into the mixed EHL model and the wear model, allowing recalculation of the lubrication characteristics and the corresponding tooth surface wear depth. This process is repeated cyclically until the number of wear cycles reaches the predetermined threshold, ultimately obtaining the cumulative tooth surface wear depth after the specified number of cycles.

Figure 4 Meshing characteristics of helical gears.

Table 1 Parameters of helical gears' geometry, lubricant, and working conditions.

4.1 Tooth surface wear depth distribution

Figure 4 shows the distribution of contact line length, tooth load, relative sliding velocity, and relative sliding distance of helical gear transmission under quasi-static loads. Figure 4a shows that during the meshing transmission of the gear pair, both the single contact line length and the total contact line length change continuously with the meshing time. From the meshing-in to meshing-out process, the length of single contact line gradually increases at first, remains unchanged in the middle meshing area, and then gradually decreases. The total contact line length varies periodically throughout the meshing process. Affected by the variation in contact line length, the tooth surface load of helical gears changes continuously, as seen in Fig. 4b. The relative sliding velocity u_s and relative sliding distance S are important factors affecting the tooth surface wear depth, and they are relatively large at both end positions while smaller near the pitch position, as seen in Fig. 4c and d.

Figure 5 Distribution of parameters affecting the tooth surface wear.

The tooth surface wear depth is a straightforward function of the average contact pressure, asperity load ratio, frictional film defect, and relative sliding distance. The relative sliding velocity and interface flash temperature are important factors influencing the frictional film defect. Therefore, the variation laws of the parameters related to the tooth surface wear depth of helical gears were investigated, as seen in Fig. 5. Figure 5a shows that the average contact pressure across the meshing tooth surfaces exhibits time-varying characteristics, and the contact pressure near the meshing-in position is significantly higher than that near the meshing-out position. Influenced by the contact pressure, the central oil film thickness at the meshing-out position is significantly higher than that at the meshing-in position, as presented in Fig. 5b. The film thickness ratio is the ratio of the minimum oil film thickness to the tooth surface roughness, and its distribution law is similar to the central oil film thickness, as illustrated in Fig. 5c. Under the working conditions specified in this paper, the value of the film thickness ratio is from 1.9323 to 2.5297, indicating that the helical gear transmission is in the mixed EHL conditions. In Fig. 5d, the asperity load ratio distribution is exactly opposite to the distribution of central oil film thickness. During the meshing-in to meshing-out process, the asperity load ratio decreases firstly and then increases, but the increase is relatively small. The relative sliding velocities near the engaging and disengaging ends are relatively larger and smaller near the pitch position, resulting in a “V” shaped distribution of the tooth surface flash temperature of the helical gear, as shown in Fig. 5e. The frictional film defect correlates with the relative sliding velocity and surface flash temperature; this makes the frictional film defect near the pitch position relatively large, as illustrated in Fig. 5f.

Figure 6 The tooth surface wear depth distribution of helical gears.

Figure 6 presents the distribution of tooth surface wear depth in the helical gear transmission under the mixed EHL conditions after 1 × 10⁴ load cycles. It is evident from the figure that within the entire meshing region, the wear depth on the tooth surface of the pinion and the gear presents a non-uniform distribution pattern. The two gears meshed with each other have greater wear depth near the root and top meshing positions and smaller near the pitch position. The maximum tooth surface wear depth of the pinion occurs at the root engagement position, while the gears' maximum wear depth occurs at the top engagement position. In this paper, the transmission ratio of helical gears is 1.4. The number of meshing times of the pinion and the gear is 1 × 104 and 0.72 × 104, respectively, and the pinion has far more meshing cycles than the gear, resulting in a greater tooth surface wear depth.

Figure 7 Comparison of tooth surface wear depth under mixed EHL conditions and dry conditions.

4.2 Wear depth distribution of helical gears under different lubrication conditions

To investigate the influence of lubrication conditions on tooth surface wear characteristics, Fig. 7 compares the wear depth of helical gear tooth surfaces under mixed EHL and dry contact conditions with the same geometric parameters and operating conditions. The wear depth under dry contact is calculated using the classical Archard wear model. As shown in the figure, the distribution patterns of wear depth for both the pinion and gear under mixed EHL are generally consistent with those under dry contact. However, the wear depth under mixed EHL is significantly smaller than that under dry contact, with a difference of nearly 4 orders of magnitude. This discrepancy arises because, under dry contact, the lack of an effective lubricating oil film between meshing tooth surfaces leads to concentrated contact stress and significant frictional heat generation, resulting in severe tooth surface wear dominated by adhesive and abrasive wear mechanisms. In contrast, mixed EHL reduces the wear coefficient and suppresses tooth surface temperature rise by separating the tooth surfaces with a lubricating film, thereby mitigating wear severity. This study not only validates the accuracy of the proposed wear model for helical gears under mixed EHL but also quantitatively demonstrates the remarkable effect of proper lubricant application in reducing tooth surface wear, providing a theoretical basis for gear lubrication design.

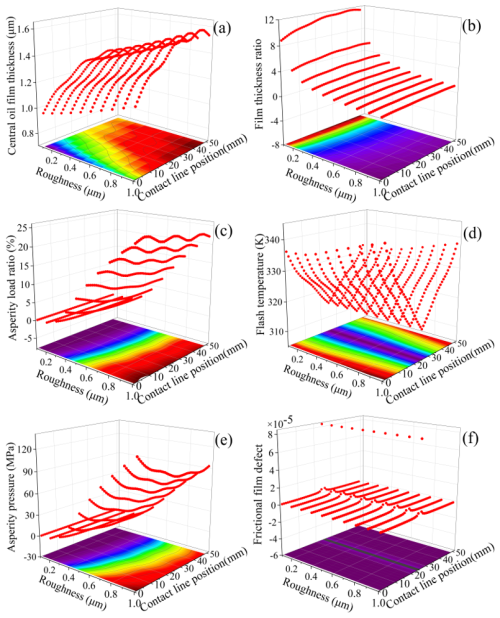
Figure 8 Variation of lubrication parameters between meshing tooth surfaces at different roughnesses.

Load directly acting on the asperities of the surface is the principal factor leading to tooth surface wear; tooth roughness is the main factor affecting the lubrication state between meshing tooth faces (Chen et al., 2024). Therefore, to study the tooth surface wear under different lubrication states, this paper first investigated the variation of relevant lubrication parameters between meshing tooth faces under different roughness conditions, as can be seen in Fig. 8. In Fig. 8a, with the increase in the tooth surface roughness, the central oil film thickness between meshing tooth surfaces also increases successively. Figure 8b and c illustrate the distribution of film thickness ratio Λ and asperity load ratio L_a under different roughness conditions, respectively. When the roughness σ is in the range of 0.1–0.3 µm, Λ varies between 3 and 11.6, and the maximum L_a is 1.3 %. The asperities hardly participate in the contact, and the helical gear pair is close to full-film lubrication. When σ is in the range of 0.4–1 µm, Λ varies between 1 and 3.1, and the L_a varies from 1.5 % to 26.3 %. At this time, the helical gear pair is in the mixed EHL conditions. This shows that the roughness can change the lubrication state between the meshing tooth surfaces, and the lubrication state gradually transitions from the full-film lubrication state to the mixed EHL state during the process of the roughness increasing from 0.1 to 1 µm. Under the full-film lubrication state, the difference in the flash temperatures of the tooth surfaces under different roughnesses is relatively small. However, under the mixed EHL conditions, the tooth surface flash temperature gradually increases as the surface roughness increases, as shown in Fig. 8d. This is due to the fact that both the L_a (Fig. 8c) and the asperity pressure (Fig. 8e) under the mixed EHL conditions increase with the increase in roughness, resulting in more heat generated by the frictional contact of the asperities. Figure 8f shows the variation of frictional film defect under different roughness conditions, but the variation of tooth roughness has almost no effect on the frictional film defect. According to Eq. (13), the frictional film defect is greatly affected by the relative sliding velocity and tooth surface flash temperature, but the change in tooth surface flash temperature caused by changing the value of roughness has little impact on the frictional film defect.

Figure 9 The tooth surface wear depth distribution of helical gears under different roughnesses.

Figure 9 shows the tooth surface wear depth distribution of helical gears under different roughness conditions. As depicted in Fig. 9a and b, when the tooth roughness goes up, the overall wear depth of the teeth on both the pinion and the gear exhibits an increasing trend. However, when the roughness is less than or equal to 0.3 µm, the helical gear pair is in an approximately full elastohydrodynamic lubrication state, at which time the change of the roughness value has a relatively small impact on the change in the tooth surface wear depth of the two gears. As depicted in Fig. 9c and d, the maximum tooth surface wear depth at the meshing positions of the tooth roots and tooth tops of the two gears was extracted. The analysis reveals that, under the working conditions defined in this research, the variation range of the wear depth at the meshing position of the pinion's tooth root is remarkably greater than that of the pinion's tooth top. When the roughness is less than or equal to 0.7 µm, the surface wear depth of the gear at the tooth root's meshing position is lower than that at the tooth top's meshing position. With the continuous increase in the roughness, the wear depth at the meshing position of the gear's tooth root gradually gets larger than that at the meshing position of the tooth top. This research indicates that the distribution of the tooth surface wear can be affected by the lubrication condition between the meshing tooth surfaces, good lubrication can effectively reduce tooth surface wear, and a large tooth roughness will accelerate the tooth surface wear process.

Figure 10 Effects of different factors on pinion tooth surface wear.

4.3 Influence of different factors on the helical gear tooth surface wear depth

Figure 10 shows the influence of the geometric parameters and working condition parameters of helical gears on tooth surface wear in the mixed EHL conditions. In Fig. 10a, with the increase in the module, the tooth surface wear depth of the pinion decreases gradually. This owes to an increase in the module results in an enlargement of the comprehensive curvature radius, which in turn causes a reduction in the tooth surface contact pressure induced by the normal load. According to the display in Fig. 10b and c, as the tooth width and helix angle increase, the tooth surface wear depth gradually diminishes. This arises from the increase in tooth width and the helix angle extending the contact line length, reducing the unit line load, and the average contact pressure acting on the contact line can consequently lower the tooth surface wear depth. Figure 10d shows the tooth surface wear depth of the pinion decreases with the increase in rotational velocity, and the impact of velocity changes on the tooth surface wear depth gradually decreases under high-speed working conditions. This is because the increase in rotational velocity leads to a greater amount of oil being entrapped between the meshing tooth surfaces; this leads to an increase in the thickness of the oil film and a decrease in the asperity load ratio, thereby reducing the tooth surface wear depth. However, the increase in rotational velocity also leads to an increment of the heat generated between the meshing tooth surfaces, which suppresses the increase in the oil film thickness. The higher the rotational velocity, the more heat is generated and the stronger the inhibitory effect on the increase in the oil film thickness. As shown in Fig. 10e, an increase in input torque raises the normal load on the tooth surface. Consequently, the unit line load, tooth contact pressure, and asperity load all increase, causing the gear's tooth surface wear depth to rise with the torque increase. Figure 10f shows the distribution of the pinion's tooth surface wear depth under various tooth hardness conditions. As is observable from the figure, with the augmentation of the tooth surface hardness, the wear depth of the pinion tooth surface exhibits a gradually diminishing trend. Additionally, alterations in the aforementioned parameters have a relatively obvious impact on the wear depth where the tooth root meshes but have a relatively limited impact on other meshing positions.

5 Conclusion

The average contact pressure of helical gears near the meshing-in position is significantly higher than that near the meshing-out position. The central oil film thickness and film thickness ratio show similar patterns, rising first and then falling from meshing in to meshing out. The asperity load ratio varies inversely to the ratio of the film thickness. The surface flash temperature peaks near meshing in and meshing out, while the frictional film defect is maximal near the pitch position.

Under the mixed EHL conditions, the distribution of tooth surface wear depth for helical gears is not uniform. The wear depths near the tooth root and the top regions of both the pinion and the gear exceed those near the pitch position, and the maximum tooth surface wear depth appears at the root of the pinion. Affected by the number of meshing cycles, the wear depth on the tooth surface of the pinion is greater than that of the gear.

The distribution of wear depth on helical gear tooth surfaces under the mixed EHL conditions and the dry contact state is basically consistent, but the tooth surface wear depth under the mixed EHL conditions is about 4 orders of magnitude lower than that in the dry contact state. Tooth surface roughness influences tooth surface wear distribution by modifying the lubrication state between meshing tooth surfaces. Specifically, reduced tooth surface roughness not only enhances the lubrication performance at the meshing interface, but also effectively slows the progression of tooth surface wear.

Changes in the tooth profile and operating parameters of helical gears can affect the tooth surface wear depth under mixed lubrication conditions. Specifically, the tooth surface wear depth decreases with the increase in the module, face width, helix angle, rotational velocity, and tooth surface hardness, while it increases with the increase in torque. Furthermore, the variations in the aforementioned parameters exert a notably greater impact on the tooth surface wear depth at the meshing position of the pinion's root.