Effect of the gap between the diffuser blade and impeller blade on the internal complex flow and aerodynamic performance of a centrifugal compressor

In this paper, the impact of the ratio (R_d= $R_{\mathrm{2}}/R_{\mathrm{1}}$) between the diffuser inlet radius (R₂) and the impeller outlet radius (R₁) on internal complex flow and the aerodynamic performance of a centrifugal compressor is deeply studied through numerical simulations. The study investigates how variations in R_d affect the efficiency, differential pressure and minimum allowable mass flow rate of the compressor. The difference in pressure, velocity and turbulent kinetic energy of the centrifugal compressor is demonstrated at three different values of R_d. Additionally, the spatiotemporal evolution of the complex internal flow of the centrifugal compressor is captured under an unsteady operational state. The characteristics of pressure and velocity fluctuations in the centrifugal compressor are deeply analyzed by fast Fourier transform (FFT) spectral analysis, which reveals that with increasing R_d, the intake conditions are significantly improved at the diffuser inlet. The findings offer physical insights into enhancing the efficiency and lowest allowable mass flow rate of the centrifugal compressor by minimizing energy loss from airflow impacting the diffuser blades.

1 Introduction

Centrifugal compressors are widely utilized in a variety of industrial fields, including coal, power and petrochemicals, owing to their excellent efficiency and reliability. Diffusers are a crucial component of centrifugal compressors and have the capacity to significantly increase the pressurization efficiency of the compressor. Diffusers are commonly classified into two types: vaned and vaneless. The former have a greater capacity for pressurization and a more compact construction. The airflow distribution at the impeller outlet is uneven, both in the circumferential and width directions, which affects the diffuser blades. A small gap between the impeller and vaned diffuser improves the intake conditions at the diffuser inlet domain. The aerodynamic performance of a centrifugal compressor is influenced by the gap size. The purpose of this paper is to clarify the effect of gap size on the aerodynamic performance of centrifugal compressors using numerical simulation.

Numerous studies have focused on understanding the physical mechanisms by which diffusers impact centrifugal compressors. Lawless (1994) and Zhang et al. (2020) investigated how vaneless and vaned diffusers influence rotating stalls in centrifugal compressors and through air injection to control it. Engeda (1997) studied three different types of diffusers (vaneless diffuser, conventional vaned diffuser and low solidity vaned diffuser) that affect the rotating stall and surge characteristics of centrifugal compressors. Skoch (2003, 2005) and Spakovszky (2004) explored the rotating stall in high-speed centrifugal compressors, enhancing the stability of centrifugal compressors through air injection. Han et al. (2014) employed numerical simulations to analyze the rotating stalls of centrifugal compressors equipped with vaned diffusers. The results showed that the geometry of the diffusers significantly influences the aerodynamic performance of centrifugal compressors. Justen et al. (1999) utilized experimental methods to investigate the unsteady flow phenomena in centrifugal compressors with variable-geometry vaned diffusers. Hildebrandt and Genrup (2007) investigated how changes in back sweep angles and width affect flow patterns at the outlet of centrifugal compressors with vaneless diffusers. Numerous studies have examined various geometries, including leading-edge slotted, half-guide vaned, pipe and low solidity vaned diffusers, to enhance diffuser performance (Zhang et al., 2019; Yoshinaga et al., 1987; Reeves, 1977; Mukkavilli et al., 2002). Li et al. (2023a) investigated the impact of boundary conditions on the diffuser with non-uniform velocity on the characteristics of the jet and the internal flow field. Li et al. (2022) investigated new design principles for the vaned diffusers and proposed some design reference principles for it. Engeda and Messele (2018) and Wang et al. (2018) applied intelligent methods to optimize three-dimensional vaned diffusers, although these techniques are difficult to implement in industrial settings. Kim et al. (2008) compared three vaned diffuser types, finding that the NACA 65-4A10 diffuser has better performance and satisfied a more comprehensive operating range. Zeng et al. (2023) proposed an inverse design method using the blade load distribution for diffuser design, although its application as a universal principle remains challenging.

Koth (1981) first examined the interference between the internal flows of the impeller and the vaned diffuser and discovered that the internal flow of the diffuser had a negligible effect on the impeller. Arndt et al. (1990) explored the vaned diffuser and centrifugal impeller interaction through an experimental study and discovered that the pressure fluctuation at the front of the diffuser blade decreases with increasing radial gaps between the impeller and diffuser. Justen et al. (1999) experimented by examining the effects of the installation angle and the radial position of diffuser blades on the rotor–stator interaction flow field; they found that the installation angle exerts a more significant influence on the pressure fluctuation of the flow field than the radial position. Ziegler et al. (2003a, b) investigated the interaction mechanism of the impeller-diffuser and found that it is possible to optimize the flow configuration in the diffuser channel by adjusting the radial gap ratio for each specific scenario. Boncinelli et al. (2007) conducted a numerical simulation to examine the interaction between the impeller and diffuser by utilizing experimental data from existing literature to aid their investigation. The numerical simulation results are highly consistent with Ziegler's experimental results. Xue et al. (2019) conducted multi-position dynamic pressure measurements on an industrial centrifugal compressor equipped with a variable vaned diffuser through experiments and simulations, and there was a small error between the experimental results and the simulation results. Chen et al. (2021) investigated the influence of the diffuser-to-impeller gap length on centrifugal compressor performance and found that a suitable extension of the gap length will positively impact the aerodynamic performance of the centrifugal compressor. However, excessive gap length will reduce the aerodynamic performance of the compressor. Liu et al. (2025) developed a novel CFD model for centrifugal pump impeller angular misalignment, quantifying progressive hydraulic degradation and amplified radial forces/pressure pulsations, validated via pump performance curves. Xu et al. (2022) established a flexible rotor dynamics model integrating unbalanced mass effects and bearing forces. They experimentally verified the frequency prediction accuracy and captured nonlinear vibration transitions in rotating systems.

The comprehensive literature review and observations indicate that the geometry of the diffuser and its interaction with the impeller significantly influence the aerodynamic performance of centrifugal compressors. While prior studies have established the general trend that larger radial gaps R_d improve flow uniformity and compressor stability, this study provides three novel insights: first, increasing R_d ($\mathrm{1.06}\le R_{\mathrm{d}}\le \mathrm{1.14}$) significantly suppresses low-velocity zones at the impeller outlet, thereby enhancing flow uniformity in both the impeller and diffuser domains. Second, when R_d=1.14, high turbulent kinetic energy regions at the diffuser inlet are eliminated, reducing energy dissipation compared to R_d=1.06. Finally, fast Fourier transform analysis proves that larger R_d attenuates pressure/velocity fluctuation amplitudes, shifting dominant frequencies toward lower harmonics.

This paper is organized as follows: in Sect. 2, the numerical models and governing equations are first briefly described. After that, the detailed steady and unsteady numerical simulation results are discussed in Sect. 3. Finally, Sect. 4 summarizes some constructive conclusions.

2 Governing equations and numerical method

2.1 Governing equations of fluid flow

The Reynolds-averaged equations, composed of the conservation laws of mass, momentum and energy, can be utilized to solve the flow field of the centrifugal compressor under steady and unsteady conditions. The three-dimensional compressible continuity equation is as follows (Li et al., 2023b):

$$\begin{array}{}\text{(1)}& {\displaystyle \frac{\partial \mathit{\rho }}{\partial t}}+{\displaystyle \frac{\mathrm{1}}{r}}\left[{\displaystyle \frac{\partial \left(\mathit{\rho }{v}_{r}r\right)}{\partial r}}+{\displaystyle \frac{\partial \left(\mathit{\rho }{v}_{\mathit{\theta }}\right)}{\partial \mathit{\theta }}}+{\displaystyle \frac{\partial \left(\mathit{\rho }{v}_{z}r\right)}{\partial z}}\right]=\mathrm{0},\end{array}$$

where ρ is density, t is time and v_r, v_θ, v_z are velocities in different directions.

The momentum conservation equation is as follows:

$$\begin{array}{}\text{(2)}& {\displaystyle }\begin{array}{rl}\mathit{\rho }\left({\displaystyle \frac{\mathrm{d}{v}_r}{\mathrm{d}t}}-{\displaystyle \frac{v_{\mathit{\theta }}^{\mathrm{2}}}{r}}\right)& =\mathit{\rho }{F}_{br}+{\displaystyle \frac{\mathrm{1}}{r}}\left[{\displaystyle \frac{\partial \left(p_{rr}r\right)}{\partial r}}+{\displaystyle \frac{\partial \left(p_r\mathit{\theta }\right)}{\partial \mathit{\theta }}}\right.\\ & \left.+{\displaystyle \frac{\partial \left(p_{rz}r\right)}{\partial z}}-p_{\mathit{\theta }\mathit{\theta }}\right],\end{array}\text{(3)}& {\displaystyle }\begin{array}{rl}\mathit{\rho }\left({\displaystyle \frac{\mathrm{d}{v}_{\mathit{\theta }}}{\mathrm{d}t}}+{\displaystyle \frac{v_r{v}_{\mathit{\theta }}}{r}}\right)& =\mathit{\rho }{F}_{b\mathit{\theta }}+{\displaystyle \frac{\mathrm{1}}{r}}\left[{\displaystyle \frac{\partial \left(p_{r\mathit{\theta }}r\right)}{\partial r}}+{\displaystyle \frac{\partial \left(p_{\mathit{\theta }\mathit{\theta }}\right)}{\partial \mathit{\theta }}}\right.\\ & \left.+{\displaystyle \frac{\partial \left(p_{\mathit{\theta }z}r\right)}{\partial z}}+p_{r\mathit{\theta }}\right],\end{array}\text{(4)}& {\displaystyle }\mathit{\rho }{\displaystyle \frac{\mathrm{d}{v}_z}{\mathrm{d}t}}=\mathit{\rho }{F}_{bz}+{\displaystyle \frac{\mathrm{1}}{r}}\left[{\displaystyle \frac{\partial \left(p_{rz}r\right)}{\partial r}}+{\displaystyle \frac{\partial \left(p_{\mathit{\theta }z}\right)}{\partial \mathit{\theta }}}+{\displaystyle \frac{\partial \left(p_{zz}r\right)}{\partial z}}\right],\end{array}$$

where p is pressure.

The total energy equation is as follows:

$$\begin{array}{}\text{(5)}& \begin{array}{rl}\mathit{\rho }{\displaystyle \frac{\mathrm{d}H}{\mathrm{d}t}}& ={\displaystyle \frac{\mathrm{1}}{r}}\left[{\displaystyle \frac{\partial \left(rK\frac{\partial T}{\partial r}\right)}{\partial r}}+{\displaystyle \frac{\partial \left(\frac{K\partial T}{r\partial \mathit{\theta }}\right)}{\partial \mathit{\theta }}}+{\displaystyle \frac{\partial \left(rK\frac{\partial T}{\partial r}\right)}{\partial z}}\right]\\ & +\mathit{\rho }q+{\displaystyle \frac{\mathrm{d}p}{\mathrm{d}t}}+\mathit{\phi },\end{array}\end{array}$$

where K is the heat transfer coefficient of the fluid medium.

2.2 Turbulence model

In this study, the SSTk−ω turbulence model is implemented in the numerical simulations. The SST model utilizes the k−ω model near the wall and transitions to the k−ε model as it moves away from the boundary layer through a blending function. Bourgeois et al. (2014) determined the accuracy of the SST model, the SST-reattachment modification (RM) model, the k−e model, and the Speziale, Sarkar and Gatski Reynolds stress model (RSM-SSG). Their analysis identified the SST model as being suitable to predict the compressor performance (Ma et al., 2021; Zeng et al., 2023). The SSTk−ω turbulence model is mainly composed of turbulent kinetic energy and the specific dissipation rate; the expression is as follows (Li et al., 2024):

$$\begin{array}{}\text{(6)}& {\displaystyle \frac{D\left(\mathit{\rho }k\right)}{Dt}}=\underset{A}{\underbrace{P_k}}-\underset{B}{\underbrace{{\mathit{\beta }}^{\ast }\mathit{\rho }\mathit{\omega }k}}+\underset{C}{\underbrace{{\displaystyle \frac{\partial }{\partial x_j}}\left[(\mathit{\mu }+{\mathit{\sigma }}_k\mathit{\mu }{}_t){\displaystyle \frac{\partial k}{\partial x_j}}\right]}},\text{(7)}& {\displaystyle }\begin{array}{rl}{\displaystyle \frac{D\left(\mathit{\rho }\mathit{\omega }\right)}{Dt}}& =\underset{A{}^{\prime }}{\underbrace{{\displaystyle \frac{\mathit{\gamma }}{v_t}}{P}_k}}-\underset{B{}^{\prime }}{\underbrace{\mathit{\beta }\mathit{\rho }{\mathit{\omega }}^{\mathrm{2}}}}+\underset{C{}^{\prime }}{\underbrace{{\displaystyle \frac{\partial }{\partial x_j}}\left[(\mathit{\mu }+{\mathit{\sigma }}_{\mathit{\omega }}\mathit{\mu }{}_t){\displaystyle \frac{\partial \mathit{\omega }}{\partial x_j}}\right]}}\\ & +\underset{D}{\underbrace{\mathrm{2}(\mathrm{1}-F_{\mathrm{1}}){\displaystyle \frac{\mathit{\rho }{\mathit{\sigma }}_{\mathit{\omega }\mathrm{2}}\partial k\partial \mathit{\omega }}{\mathit{\omega }\partial x_j\partial x_j}}}},\end{array}\end{array}$$

where k is the turbulent kinetic energy; ω is the specific dissipation rate; β^∗, σ_k, γ, β, σ_ω, and ${\mathit{\sigma }}_{{\mathit{\omega }}^{\mathrm{2}}}$ are constants; μ_t is the kinetic viscosity; and F₁ is the mixing functions. v_t is the kinematic eddy viscosity, the expression of which is as follows:

$$\begin{array}{}\text{(8)}& {\displaystyle }{v}_t={\displaystyle \frac{a_{\mathrm{1}}k}{max(a_{\mathrm{1}}\mathit{\omega };S{F}_{\mathrm{2}})}},\text{(9)}& {\displaystyle }S=\sqrt{\mathrm{2}{S}_{ij}{S}_{ij}},S_{ij}={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}\left({\displaystyle \frac{\partial u_i}{\partial x_j}}-{\displaystyle \frac{\partial u_j}{\partial x_i}}\right),\end{array}$$

where a₁ is the structural parameter, the value of which is 0.31, and F₂ is the boundary layer mixing function.

$$\begin{array}{}\text{(10)}& {\displaystyle }{P}_k={\mathit{\tau }}_{ij}{\displaystyle \frac{\partial u_i}{\partial x_j}}\text{(11)}& {\displaystyle }{\mathit{\tau }}_{ij}={\mathit{\mu }}_t\left(\mathrm{2}{\mathrm{\Omega }}_{ij}-{\displaystyle \frac{\mathrm{2}\partial u_k}{\mathrm{3}\partial x_k}}{\mathit{\delta }}_{ij}\right)-{\displaystyle \frac{\mathrm{2}}{\mathrm{3}}}\mathit{\rho }k{\mathit{\delta }}_{ij}\text{(12)}& {\displaystyle }{\mathrm{\Omega }}_{ij}={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}\left({\displaystyle \frac{\partial u_i}{\partial x_j}}+{\displaystyle \frac{\partial u_j}{\partial x_i}}\right)\end{array}$$

Here, u_i is the velocity vector in the x direction in Cartesian coordinates, τ_ij is the Reynolds stress and δ_ij is the Kronecker symbol. The model constants are calculated by the mixing function F₁, which is expressed as follows:

$$\begin{array}{}\text{(13)}& \mathit{\varphi }=F_{\mathrm{1}}{\mathit{\varphi }}_{\mathrm{1}}+(\mathrm{1}-F_{\mathrm{1}}){\mathit{\varphi }}_{\mathrm{2}},\end{array}$$

where ϕ₁ is the model constant of the k−ω original model, ϕ₂ is the model constant of the k−ω standard model and ϕ is the model constant of the SST turbulence model. Other correlation functions are expressed as follows:

$$\begin{array}{}\text{(14)}& {\displaystyle }{F}_{\mathrm{1}}=\tanh \left\{{\left\{min\left[max\left({\displaystyle \frac{\sqrt{k}}{{\mathit{\beta }}^{\ast }wy}},{\displaystyle \frac{\mathrm{500}v}{y^{\mathrm{2}}\mathit{\omega }}}\right),{\displaystyle \frac{\mathrm{4}{\mathit{\sigma }}_{\mathit{\omega }\mathrm{2}}k}{C{D}_{k\mathit{\omega }}{y}^{\mathrm{2}}}}\right]\right\}}^{\mathrm{4}}\right\},\text{(15)}& {\displaystyle }{F}_{\mathrm{2}}=\tanh \left[{\left[max({\displaystyle \frac{\mathrm{2}\sqrt{k}}{{\mathit{\beta }}^{\ast }wy}},{\displaystyle \frac{\mathrm{500}v}{y^{\mathrm{2}}\mathit{\omega }}})\right]}^{\mathrm{2}}\right],\text{(16)}& {\displaystyle }C{D}_{k\mathit{\omega }}=max(\mathrm{2}{\displaystyle \frac{\mathit{\rho }{\mathit{\sigma }}_{\mathit{\omega }\mathrm{2}}\partial k\partial \mathit{\omega }}{\mathit{\omega }\partial x_j\partial x_j}},{\mathrm{10}}^{-\mathrm{20}}),\end{array}$$

where v is the viscosity coefficient of molecular motion and y is the minimum distance to the wall.

2.3 Geometry and mesh generation

The centrifugal compressor model used in this study was simplified to include only the impeller, diffuser and volute. The main geometrical parameters of the simplified centrifugal compressor are shown in Table 1.

Table 1 Main geometrical parameters of the compressor.

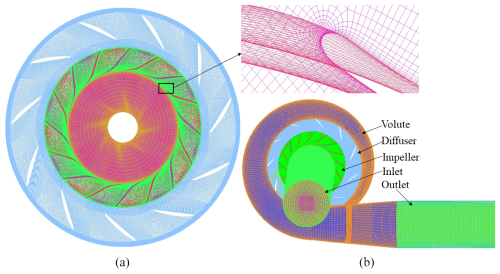
Figure 1 Mesh of the centrifugal compressor: (a) impeller and diffuser and (b) whole computational domain.

In addition to mesh division for the impeller, diffuser and volute, necessary extensions at the inlet and outlet are essential to accurately define the boundary conditions. The whole computational domain is shown in Fig. 1.

Figure 1 shows the mesh of the centrifugal compressor. Figure 1a shows the mesh of the impeller and diffuser, as well as some detailed views of the impeller. Figure 1b shows the entire numerical simulation model. The green part at the top of the impeller is the extended inlet computational domain, and the green part at the volute outlet is the extended outlet computational domain. To improve the quality of the numerical simulation and obtain accurate information about the flow field, the mesh near the wall of the blade, which is displayed in an enlarged view, represents densification. In this research, the meshes of all components for the compressor are structured meshes.

The designed rotation speed and mass flow rate of the centrifugal compressor used in this numerical simulation are 18 000 rpm and 0.47 kg s⁻¹, respectively. To investigate the relationship between the distance between the impeller blades and the diffuser and its effect on the aerodynamic performance of the compressor, three different diffusers were examined in a numerical model.

In the numerical simulation of centrifugal compressors, refinement of near-wall grids is crucial to ensure that y⁺ values meet the requirements of the SST k−ω model in ANSYS CFX (Ekradi and Madadi, 2020; Liu et al., 2022). The height of the first grid layer was set to $\mathrm{5}\times {\mathrm{10}}^{-\mathrm{6}}$ m, whereby y⁺ values throughout the computational domain are all less than 5.

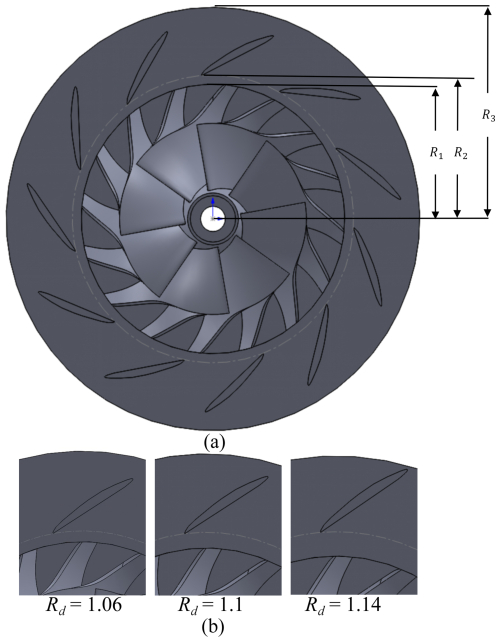
Figure 2 Relative position relationship of impeller and diffusers with three different R_d values: (a) impeller and diffuser and (b) three different diffusers.

Figure 2 depicts the relative position relationship of the impeller and diffusers with three different R_d values. Figure 2a shows the impeller and the diffuser, where R₁ represents the outlet radius of the impeller, R₂ represents the inlet radius of the vaned diffuser and R₃ represents the outlet radius of the vaned diffuser. R₁ and R₃ are constants, and $R_{\mathrm{d}}=R_{\mathrm{2}}/R_{\mathrm{1}}$ is a dimensionless parameter that indicates the gap size between the impeller and vaned diffuser. Figure 2b exhibits the relative position of the impeller and diffuser for R_d values of 1.06, 1.1 and 1.14.

The radial gap ratios (R_d=1.06, 1.10, 1.14) represent three critical design philosophies within the dominant industrial range ($\mathrm{1.06}\le R_{\mathrm{d}}\le \mathrm{1.14}$). The lower bound R_d=1.06 approaches structural limits for compact configurations, below which blade vibration amplification and premature rotating stall occur. The upper bound R_d=1.14 corresponds to efficiency-optimized designs where further clearance expansion incurs casing size penalties and diffusion efficiency degradation.

2.4 Simulation settings

In this paper, all numerical simulations are carried out using the software ANSYS CFX 2022 R1. Throughout these simulations, the SST turbulent model is employed. The fluid medium selected is the ideal gas, with the reference pressure set to 0. At the boundary conditions, a non-slip boundary and a smooth wall are adopted, and the heat transfer is configured as adiabatic. For the inlet boundary condition, the total pressure and total temperature are specified, with values of 101 325 Pa and 288.15 K, respectively. The simulation environment is closely aligned with that of Li et al. (2024).

Figure 3 Validation of mesh independence.

2.5 Verification of mesh independence

The accuracy of numerical simulations depends on the mesh quantity and quality. The mesh quality in this study exceeds 0.3, ensuring the accuracy of the numerical simulation. Increasing the number of meshes in the model enhances detail accuracy, but too many meshes will slow down the simulation. Therefore, it is imperative to conduct mesh independence tests to achieve an optimal equilibrium between computational fidelity and velocity.

Figure 3 illustrates the isentropic efficiency and pressure difference for six groups with varying grid numbers at the designed mass flow rate and R_d=1.1. The details of the mesh number for different components are shown in Table 2.

Table 2 Details of the mesh numbers for different components.

When the number of mesh cells is 1.63 million, the isentropic efficiency is 81.3 % and the pressure difference is 14.95 kPa. When the mesh resolution is increased to 3.0 million, the above values rise to 82.22 % and 15.25 kPa, respectively. Further refining the mesh to 3.79 million results in negligible changes. Therefore, when the number of mesh cells exceeds 3.0 million, its impact on the isentropic efficiency and pressure difference is negligible. Based on this result, 3.0 million mesh cells will be adopted in subsequent numerical simulations.

Figure 4 Polytropic efficiency and pressure differential curves of the centrifugal compressor: (a) polytropic efficiency curves and (b) pressure difference curves.

3 Numerical results and discussions

3.1 External characteristics of the centrifugal compressor

R_d is a crucial dimensionless parameter for a vaned diffuser equipped with centrifugal compressors. To investigate the effect of R_d on compressor aerodynamic performance, centrifugal compressors with three different R_d values were examined using numerical simulation.

Figure 4 presents the polytropic efficiency and the pressure differential curves for the centrifugal compressor. Figure 4a shows three polytropic efficiency curves: the blue curve denotes R_d=1.06, the red curve denotes R_d=1.1 and the yellow curve denotes R_d=1.14. The optimum efficiency point for all R_d values occurs at Q=0.47, which is consistent with the design. At the same mass flow rate, the polytropic efficiency of the compressor was determined to be maximum at R_d=1.14 and minimum at R_d=1.06 for the compressor. Figure 4b shows the pressure difference curves for the centrifugal compressor at three R_d values. R_d=1.14 yields the highest pressure difference, and R_d=1.06 results in the lowest at the same mass flow rate. As marked as the minimum allowable flow rate in the three curves, the minimum allowable mass flow rate is Q=0.41, 0.39 and 0.37 at R_d=1.06, 1.1 and 1.14, respectively. Consequently, the minimum allowable flow rate decreases as R_d increases.

The analysis of Fig. 4 shows that the polytropic efficiency and the pressure difference of the centrifugal compressor increase with increasing R_d at the same mass flow rate, and the minimum allowable mass flow rate of the centrifugal compressor decreases with increasing R_d. It is obtained that raising the value of R_d from 1.06 and 1.14 greatly enhances the aerodynamic performance of the compressor and increases its operating range, in alignment with the findings of Chen et al. (2021).

Figure 5 Velocity and streamline for ZX axial section: (a) position of the section, (b) R_d=1.06, (c) R_d=1.1 and (d) R_d=1.14.

3.2 Axial and circumferential analysis of the velocity and pressure fields

Airflow from the impeller outlet is unevenly distributed, circumferentially and widthwise, impacting the vaned diffuser blades and causing impact losses.

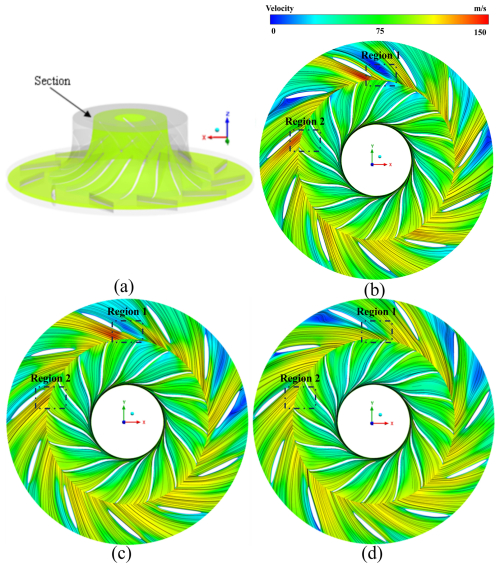
Figure 6 Velocity streamline for the circumferential cross-section: (a) position, (b) R_d=1.06, (c) R_d=1.1 and (d) R_d=1.14.

Figure 5 illustrates the velocity and streamline distributions at the axial interface for Q=0.47. Figure 5a shows the location of the section. The streamline and velocity distributions for R_d=1.06, 1.1 and 1.14 are presented in Fig. 5b, c and d, respectively. This analysis focuses on the variations in velocity and streamline patterns across three different R_d values in regions 1 and 2. In region 1, for R_d=1.06, there is a significant loss of energy in the mainstream resulting from low-velocity zones on the pressure surface of the blades caused by the uneven distribution of airflow width at the impeller outlet. At R_d=1.1, uneven distribution of the airflow at the impeller outlet in the width direction is improved, although the low velocity persists on the pressure surface of the vaned diffuser blades. As R_d increases to 1.14, airflow from the impeller outlet becomes uniform, and the low-speed airflow mass disappears. In region 2, The shape of the vaned diffuser primarily influences the velocity and streamline distributions. At R_d=1.06, the diffuser blade causes fluctuations in airflow velocity in the affected section. As the diffuser blade extends outward for R_d=1.1 and R_d=1.14, its influence on the flow field velocity diminishes due to the increased distance from the section.

Figure 6 indicates the velocity and streamline distributions at the circumferential section at 50 % blade height for Q=0.47. Figure 6a shows the location of the cross-section in the centrifugal compressor. Figure 6b, c and d present the streamline and velocity distributions for R_d values of 1.06, 1.1 and 1.14, respectively. As shown in Fig. 6b, it is easily observed that many low-velocity regions and high-velocity regions in the flow passage of the diffuser obstruct the mainstream and lead to energy losses. As shown in Fig. 6c, one can see that when R_d increased to 1.1, the regions of low-velocity airflow and the high-velocity region significantly decreased but still exist in region 1 and region 2. These internal flow phenomena reveal the internal mechanism of efficiency increase and operating margin widening with the increase in R_d. Additionally, low-velocity airflow on the suction surface of the trailing edge in the impeller domain for R_d=1.06, which obstructed the airflow in the impeller domain, is newly found. As R_d increases to 1.1, the low-velocity airflow gradually disappears.

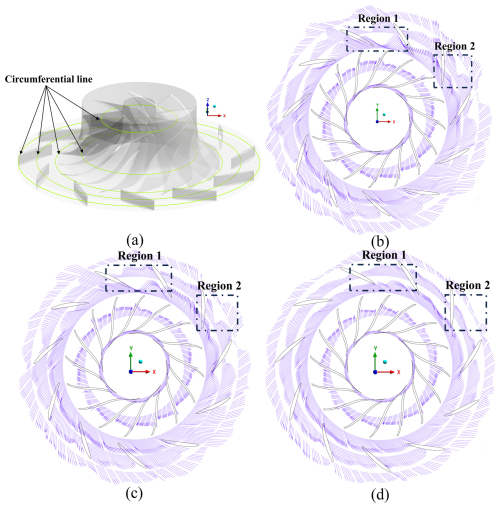
Figure 7 Absolute velocity vector for the circumferential line: (a) position of the circumferential line, (b) R_d=1.06, (c) R_d=1.1 and (d) R_d=1.14.

In region 1, plotted in Fig. 6d, the high-velocity region and low-velocity region in the diffuser domain noticeably decrease as R_d increases to 1.14, and the flow paths of the diffuser exhibit good overall permeability. The low-velocity airflow on the suction surface of the trailing edge in the impeller domain disappears, and the airflow in the impeller outlet becomes uniform. Increased R_d provides sufficient diffusion length for impeller wake energy dissipation before entering the diffuser passage. This mitigates jet-wake distortion impacts on the diffuser blades, as evidenced by suppressed velocity gradients in the circumferential distributions.

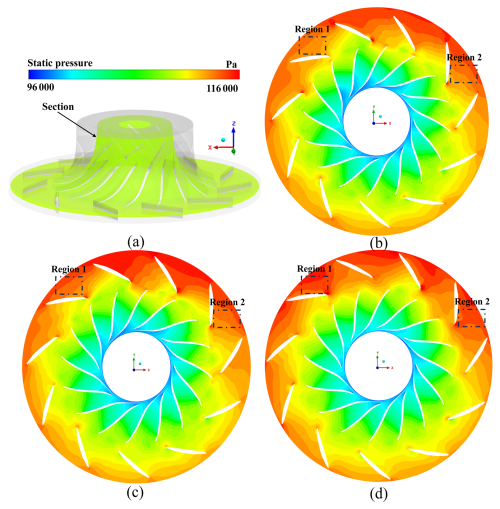
Figure 8 Static pressure for the circumferential section: (a) position of the section, (b) R_d=1.06, (c) R_d=1.1 and (d) R_d=1.14.

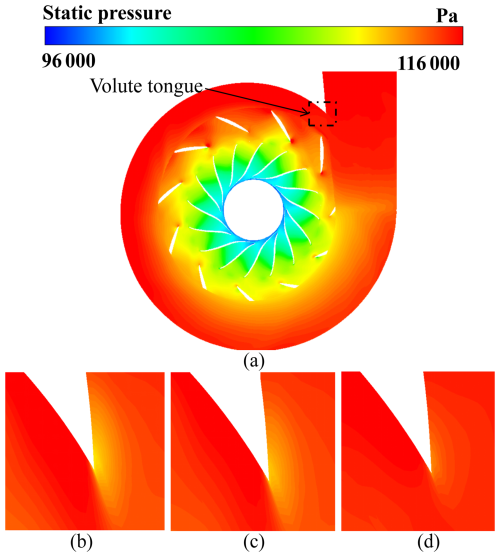
Figure 9 Pressure field near the volute tongue for different R_d values: (a) position of the section, (b) R_d=1.06, (c) R_d=1.1 and (d) R_d=1.14.

An analysis of the absolute velocity vectors is carried out to further understand the mechanism of the influence of R_d on the internal flow of centrifugal compressors. Figure 7 depicts the distribution of the absolute velocity vector at the circumferential section at 50 % blade height for Q=0.47. Figure 7b, c and d present distributions of the absolute velocity vectors for R_d values of 1.06, 1.1 and 1.14, respectively. The arrow and its length indicate the magnitude and direction of the absolute velocity. The distribution of velocity vectors offers an intuitive understanding of internal flow separation in the impeller and diffuser. It is evident by examining the diffuser's absolute velocity vector distribution that changing R_d causes the absolute velocity vector distributions to fluctuate significantly. Figure 7b displays the uneven distribution of absolute velocity vectors around the circumference of the impeller outlet. There might be inhomogeneous airflow in region 1, which could affect losses on the diffuser blades owing to the absolute velocity vector being shorter in length on the suction side and greater in length on the pressure side of the diffuser blade. Similarly, in region 2, the distribution of absolute velocity vectors in the middle of the diffuser is not uniform. As displayed in Fig. 7c, there is gradual uniformity in the absolute velocity vector distribution within the diffuser, although the airflows in regions 1 and 2 are still not uniform. As R_d increases to 1.14, Fig. 7d shows that the absolute velocity vector distribution at the inlet becomes more uniform, aligning closely with the diffuser blade design, and noticeably reduces fluctuations within the diffuser. The improved flow uniformity at larger R_d stems from reduced impeller wake distortion. At R_d=1.06, jet-wake structures directly impact the diffuser blades, creating secondary flows (region 1). Larger R_d allows wake dissipation before diffuser entry, enabling circumferential momentum redistribution.

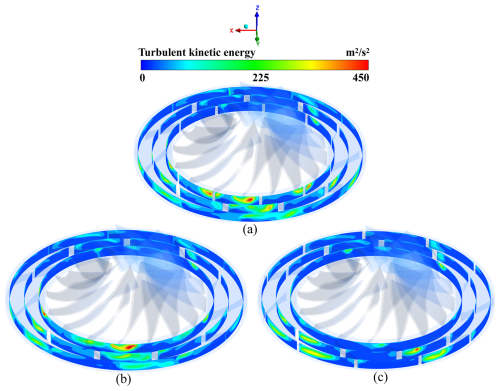
Figure 10 Circumferential surface distributions of TKE in the diffuser: (a) R_d=1.06, (b) R_d=1.1 and (c) R_d=1.14.

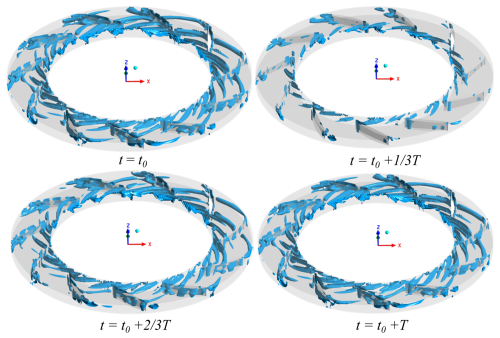
Figure 11 Temporal evolution of the vortex structure (Q-criterion) in a diffuser with R_d=1.1 and Q=0.47.

Figure 8 shows the static pressure distributions at the circumferential section at 50 % blade height for Q=0.47. The airflow entering the vaned diffuser from the impeller quickly transforms dynamic pressure into static pressure. Figure 8b, c and d present distributions of static pressure for R_d values of 1.06, 1.1 and 1.14, respectively. It is evident that an increase in R_d enhances the efficiency of converting dynamic pressure into static pressure in the airflow within the diffuser. As displayed in Fig. 8b, the static pressure is most minimal in regions 1 and 2, where the conversion efficiency is lowest. As displayed in Fig. 8c, the conversion efficiency is enhanced as R_d increases. As displayed in Fig. 8d, the conversion efficiency reaches peaks in these regions as R_d increases to 1.14. Increased R_d optimizes the coordination between the inflow direction and diffuser blade geometry, minimizing leading-edge flow separation through attenuated adverse pressure gradients. The effect is conclusively demonstrated by the elimination of low-pressure zones at the diffuser throat, where the most pronounced flow separation previously occurred under smaller R_d configurations.

Figure 12 The most and the fewest vortex structures in the diffuser region: (a) R_d=1.06, (b) R_d=1.1 and (c) R_d=1.14.

Figure 13 Locations of monitoring points for pressure and velocity measurements.

Figure 9 shows the pressure field near the volute tongue for different R_d values with Q=0.47. The non-uniform pressure field due to the volute tongue quickly decreases as R_d increases. Figure 9b, c and d present the pressure field near the volute tongue for R_d values of 1.06, 1.1 and 1.14, respectively. As displayed in Fig. 9b, the pressure field near the volute tongue fluctuates considerably. As illustrated in Fig. 9c, upon R_d reaching 1.1, a slight decline in the pressure field fluctuation near the volute tongue occurs. Further, as shown in Fig. 9d, when R_d is increased to 1.14, a substantially more pronounced reduction in the pressure field fluctuation within the identical region is evident.

Subsequent to the analysis, it is inferred that the augmentation of the R_d value facilitates the amelioration of inlet airflow conditions within the diffuser, thereby substantially mitigating the impact losses attributed to the airflow on the diffuser blades, which culminates in the amplification of the performance of the centrifugal compressor.

Figure 14 Pressure fluctuations with (a) R_d=1.06, (c) R_d=1.1 and (d) R_d=1.14.

Figure 15 Amplitude spectrum of pressure fluctuations with (a) R_d=1.06, (b) R_d=1.1 and (c) R_d=1.14.

3.3 Analysis of turbulent kinetic energy

Turbulent kinetic energy (TKE) is typically employed to evaluate the intensity of turbulent fluctuations, positively correlated with velocity fluctuations and indicative of energy dissipation in the flow region. The equation for TKE is

$$\begin{array}{}\text{(17)}& K={\displaystyle \frac{\mathrm{3}}{\mathrm{2}}}(vI{)}^{\mathrm{2}},\end{array}$$

where K represents the turbulent kinetic energy, v indicates velocity and I represent the intensity of turbulent flow.

Figure 10 displays the distribution of TKE over three circumferential surfaces within the diffuser domain for three different R_d values at Q=0.47.

Figure 10a demonstrates the turbulent kinetic energy (TKE) distribution at R_d=1.06, revealing intense energy dissipation in the circumferential section of the diffuser inlet. This phenomenon primarily stems from wake–impeller interaction suppression: close proximity amplifies impeller wake impacts on diffuser blades, generating high-shear layers and secondary flows that elevate TKE production. As R_d increases to 1.1 (Fig. 10b), TKE concentration decreases significantly due to improved flow alignment. Larger R_d allows circumferential velocity homogenization before diffuser entry, aligning inflow angles with the blade geometry. At R_d=1.14 (Fig. 10c), high TKE regions virtually disappear as energy dissipation transitions from turbulence-dominated to pressure-recovery-dominated regimes.

3.4 Unsteady flow of the centrifugal compressor

This subsection analyzes the complex internal flow characteristics of the centrifugal compressor by numerical simulation at different values of R_d. Time steps below $\mathrm{1.85}\times {\mathrm{10}}^{-\mathrm{5}}$ s (corresponding to 2° of impeller rotation) induce negligible changes in isentropic efficiency and pressure rise. Smaller steps significantly increase computational costs without improving accuracy. Therefore, this value was adopted for unsteady simulations, representing $\mathrm{2}/\mathrm{360}$ of the rotational period. The stability operation data after 16 rotations of the centrifugal compressor were chosen for data analysis to ensure the accuracy of the numerical simulation.

To precisely identify the flow-separation phenomenon in the diffuser domain, the Q-criterion was employed to analyze the spatiotemporal evolution of the vortex. The value of Q denotes the region occupied by the vorticity; a negative value indicates a region dominated by the strain rate or viscous stress (Xu et al., 2022). Therefore, the isosurfaces of the Q value can accurately represent the structure of turbulence. The equation of the Q-criterion is described as follows:

$$\begin{array}{}\text{(18)}& {\displaystyle }{\mathrm{\Omega }}_{ij}={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}\left({\displaystyle \frac{\partial u_i}{\partial x_j}}-{\displaystyle \frac{\partial u_j}{\partial x_i}}\right),\text{(19)}& {\displaystyle }{S}_{ij}={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}\left({\displaystyle \frac{\partial u_i}{\partial x_j}}+{\displaystyle \frac{\partial u_j}{\partial x_i}}\right),\text{(20)}& {\displaystyle }Q={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}\left({∥\mathrm{\Omega }∥}^{\mathrm{2}}-{∥S∥}^{\mathrm{2}}\right),\end{array}$$

where S_ij denotes the strain rate tensor and Ω_ij represents the vorticity tensor.

Figure 16 Velocity fluctuation with (a) R_d=1.06, (b) R_d=1.1 and (c) R_d=1.14.

Figure 17 Amplitude spectrum of velocity fluctuations with (a) R_d=1.06, (b) R_d=1.1 and (c) R_d=1.14.

Figure 11 captures the temporal evolution of vortex structures within the diffuser domain, revealing the complex internal flow at a Q level of 0.01. t₀ marks the moment at which the impeller completes 20 revolutions, t represents the current time and T denotes the time required for one full revolution of the impeller. Figure 11 depicts the evolution of the vortex structure distribution in the diffuser between the 20th and 21st impeller rotations. At t=t₀, the Q value was 5.06×10⁶ [s⁻²], and numerous vortices were observed simultaneously on the suction and pressure surfaces of the diffuser blades, in the flow passages, and at the diffuser inlet. These obstructions to the prevailing airflow led to energy losses. As time evolved to $t=t_{\mathrm{0}}+\mathrm{1}/\mathrm{3}T$, the Q value reached 1.38×10⁷ [s⁻²]. At this time, the vortex regions were observed to have decreased significantly compared to their state at t₀. Only a limited number of vortices were found at the diffuser inlet and along the leading and trailing edges of the vaned diffuser blades. As time evolved to $t=t_{\mathrm{0}}+\mathrm{2}/\mathrm{3}T$, the Q value decreased to 6.18×10⁶ [s⁻²], and vortices were observed to reappear in the flow passage and on both the suction and pressure surfaces of the diffuser blades, though their number remained lower than at t=t₀. At $t=t_{\mathrm{0}}+T$, the distribution of vortex structures mirrored that at t=t₀. For R_d=1.06 and R_d=1.14, the spatiotemporal evolution characteristics of the vortex structure are well consistent with $R_{\mathrm{d}}=\mathrm{1}.$1. The above phenomenon indicates that the distribution pattern of the vortex structure is periodic.

Figure 12 presents the variation in vortex structure density within the diffuser domain across different R_d values. Figure 12a, b and c depict the vortex structures for R_d=1.06, 1.1 and 1.14, respectively. Quantitative analysis revealed that the vortex density declined with increasing R_d. The maximum density occurred at R_d=1.06; the Q value min was 4.11×10⁶ [s⁻²], and the max was 1.35×10⁷ [s⁻²]. A slight decrease was evident at R_d=1.1; the Q value min was 4.20×10⁶ [s⁻²], and the max was 1.40×10⁷ [s⁻²]. The minimum vortex density was found at R_d=1.14; the Q value min was 4.24×10⁶ [s⁻²], and the max was 1.42×10⁷ [s⁻²].

Figure 13 illustrates the locations of monitoring points for measuring the pressure and velocity. Points 1 to 4 are situated in the diffuser region, 5.96 mm from the reference plane Z, while points 5 and 6 are in the volute region, 20 mm from the reference plane Z.

Figure 14 shows the pressure fluctuations and their amplitude spectrum of monitoring points at three different R_d values and Q=0.47. Figure 14a, b and c present the pressure fluctuation characteristics for R_d values of 1.06, 1.1 and 1.14, respectively. It is observed that the pressure fluctuation curves at each monitoring point exhibit periodic behavior, further verifying that the pressure fluctuations in the diffuser and the volute are periodic. The pressure fluctuations at points 5 and 6 are substantially less than those at the other monitoring locations because they are near the outlet of the volute and away from the impeller. Analyzing the variations in pressure fluctuation amplitudes at six monitoring points across three different R_d values reveals a clear trend: the pressure fluctuation amplitudes decrease as R_d increases. The above phenomena verify that the airflow becomes more uniform as R_d increases from 1.06 to 1.14.

Figure 15a, b and c present the amplitude spectrum of pressure fluctuations based on the fast Fourier transform (FFT) at monitoring points for R_d values of 1.06, 1.1 and 1.14, respectively. The x axis results from the dimensionless normalization of the frequency relative to the rotational frequency of the impeller. The y axis denotes the different monitoring points. The z axis represents the amplitude. As illustrated by the three figures above, the rotational frequency of the impeller and its multipliers are the dominant characteristic frequencies of pressure fluctuations for the monitoring points. The amplitude changes with frequency for neighboring monitoring points in Fig. 15a and b are almost identical. In Fig. 15c, the amplitudes at all monitoring points are significantly lower than in the other figures. This suggests that the stability of the pressure improves with increasing R_d.

Figure 16 shows the velocity fluctuation and the amplitude spectrum of monitoring points at three different R_d values and Q=0.47. Figure 16a, b and c present velocity fluctuation characteristics for R_d values of 1.06, 1.1 and 1.14, respectively. In Fig. 16a and c, points 5 and 6 are located close to the outflow of the volute and distant from the rotating center, experiencing a significant drop in velocity. Velocity fluctuation curves at all monitoring points exhibit periodic behavior. The fluctuation curves of points 1 and 2 are almost overlapping. In Fig. 16b, points 1 and 4 are situated on the pressure surface of the blade, while points 2 and 3 are located on the suction surface. Consequently, the average velocity at points 2 and 3 is higher than at points 1 and 4.

Figure 17a, b and c show the FFT analysis of velocity fluctuations at all monitoring points for different R_d values. The dominant characteristic frequencies are the impeller's rotational frequency and its octave, which are similar to the FFT of pressure fluctuations. The variation in amplitude at points 5 and 6 is minimal.

The spectral characteristics revealed by FFT analysis qualitatively correlate with the acoustic performance. Pressure fluctuation harmonics at blade-passing frequencies exhibit amplitude attenuation with increasing R_d, suggesting reduced discrete tone generation. Concurrently, suppression of sub-synchronous velocity fluctuation energy correlates with diminished broadband noise excitation sources. These spectral modifications align with improved flow uniformity observed in circumferential distributions, indicating potential acoustic benefit.

4 Conclusions

This study conducts numerical simulations to analyze the aerodynamic performance of the centrifugal compressor, examining both steady and unsteady flow characteristics with three different R_d values. The primary findings are outlined as follows.

First of all, the aerodynamic performance of centrifugal compressors can be significantly improved by increasing R_d, as it reduces the energy lost from airflow collisions and the structural stress carried on by airflow pulsation. Additionally, the operational range of the compressor is effectively expanded by increasing the pressure differential between the inlet and outlet of the centrifugal compressor. The impact of R_d on the aerodynamic performance of the compressor shows a high degree of consistency with previous research findings.

Furthermore, the study of the mechanism of the centrifugal compressor is mainly affected by R_d through internal flow field analysis. The velocity and streamline distributions demonstrate that with increases in R_d, as the diffuser blades extend outward, the intake conditions are enhanced and minimize the impact loss produced by the airflow colliding with the diffuser blade. In addition, a new finding is that R_d not only affects the airflow in the diffuser inlet area but also the airflow in the impeller outlet area. The distribution of static pressure shows that increasing R_d will enhance the pressurization effect in centrifugal compressors. According to the distribution of turbulent kinetic energy, the diffuser domain exhibits a notable region of high turbulence at R_d=1.06, which results in a significant loss of kinetic energy.

Finally, the temporal evolution analysis of the centrifugal compressor suggests the periodicity of the velocity and pressure. The characteristics of the pressure and velocity fluctuation distribution at various monitoring locations with varying R_d values show that increases in R_d will decrease both pressure and velocity fluctuation. Therefore, the internal complex flow characteristics of a centrifugal compressor are improved by increasing the value of R_d. In addition, the rotational frequency of the impeller and its multipliers are the dominant characteristic frequencies of pressure fluctuations, so the main noise resource of the diffuser is the rotational impeller.