Gait planning of a 4–5R rolling mechanism based on the planar 6R single-loop chain

This paper proposes a 4–5R rolling mechanism based on the spatial extension design of a planar 6R single-loop chain. By analyzing the locomotion of the planar equivalent form, a modular gait theory integrating different modes of gait with high efficiency, low energy consumption, and high speed is established. A unified kinematic strategy expression, encapsulated in the form of the gait period table, is tailored for the kinematic chain's gait on the flat terrain. A contrast gait is conducted to ascertain its velocity parameters and volatility of the center of mass (CM). By optimizing the corresponding indicators, two distinct gait patterns are achieved: a faster speed gait that prioritizes increased speed and a steady gait that emphasizes stability with reduced CM volatility. Drawing from the mobility analysis and simulation outcomes of the planar 6R single-loop kinematic chain, a theory of locomotion for a closed-chain linkage mechanism in space is proposed. A locomotion strategy on the flat ground is derived, and a unified evaluation index is proposed. Finally, the feasibility of the two working modes is verified using a physical prototype. The theoretical work in this paper simplifies the design process of closed-chain linkage robots and improves the mobility performance of closed-chain linkage robots. It lays the foundation for researching new types of closed-chain linkage robots.

1 Introduction

Mobile robots have been a substantial contributor in various sectors, including industry, service, medical, and socialization sectors (Tzafestas, 2018). The application of mobile robots has gradually extended to the research of photographic equipment carriers in ecological photography and terrain mapping engineering. Photographic robots include underwater (Debruyn et al., 2020), aerospace (Ivosevic et al., 2015), and terrestrial types (Ross et al., 2021; Mortezapoor et al., 2022). Terrestrial robots are further categorized into wheeled, tracked, footed, and closed-chain linkage types (Teng et al., 2024; Nodehi et al., 2022; Zi et al., 2024; Hu et al., 2023). Ecological photography environments are variable (Pringle et al., 2023), and traditional mobile robots present certain limitations. Among them, the closed-chain linkage can be referred to as closed kinematic chains or closed-chain mechanisms. These types of mobile robots typically consist of multiple links or modules arranged in polygon configurations and interconnected through rotating joints. Compared to open-chain robots, the moving parts of closed-chain robots can be lighter, which can lead to greater acceleration and higher efficiency of the end effector (Guo et al., 2001). Therefore, the planar 6R single-loop chain is particularly suitable for terrestrial ecological photography due to its simple structure, high motion efficiency, and operational space that mimics natural movements. The planar 6R single-loop chain is derived from the conventional six-bar mechanism. This chain eschews a rigid frame and is propelled by actively rotating joints that correspond to its degrees of freedom. Through structural and gait planning optimization, the problem of disturbing animals (Adams et al., 2022) has been effectively solved while improving the quality of captured images and videos.

Closed-chain linkage robots were proposed to solve the problems of open-chain structures with many degrees of freedom, limited stiffness, and complex control systems for footed robots (Kim et al., 2011). Typically, not all joints of closed-chain mechanisms are actuated (Ghorbel et al., 2000). Early on, Bicchi and Prattichizzo (2000) proposed kinematic manipulability indices for active and passive joints for closed-chain robots, and Mori and Omata (2002) coupled open kinematic chains and reconfigured them into closed-chain robots. The tetrahedron (TET) walker has a closed-chain linkage mechanism with good mobility (Curtis et al., 2007). To et al. (2012) proposed an improved kinematic model for calibration purposes. Nguyen et al. (2014) developed a global kinematic model to improve the position accuracy.

For partially closed-chain linkage robots, the plane of motion can be equated to a planar 6R single-loop kinematic chain. He et al. (2019) proposed adding wheels to the platform of a planar 6R single-loop kinematic chain to achieve faster speeds and spatial steering. Wang et al. (2018) proposed a multi-mode 4-RSR parallel mobile mechanism moving in a 6R chain rolling mode. Park et al. (2019) proposed a variable geometry truss robot (VGT), with a movement strategy that is similar to a planar 6R single-loop kinematic chain. Li et al. (2020) and Zhao et al. (2023) proposed a novel deformable tetrahedron rolling mechanism based on the URU branch (Li et al., 2020; Zhao et al., 2023). A novel hexagon rolling mechanism designed by Zhang et al. (2022) is driven by a central actuator. Additionally, a hexagonal kinematic chain robot has been designed to exhibit four different rolling gaits and tested experimentally (Stanley et al., 2022). While closed-chain systems have advantages over open chains in terms of rigidity of the overall mechanism, motion planning is more complex due to the need to maintain a closed-ring structure (Szynkiewicz et al., 2011).

The basic idea of a closed-chain linkage robot is to be able to achieve stable and continuous periodic movement, which requires stability criterion and gait planning. The zero moment point method (ZMP) solves the problem of discriminating the dynamic stability of a robot (Kim et al., 2018). For the closed-chain link robots, the problem of how to make the robot more stable translates into the issue of how to make the unstable state of the robot controllable. There are two research directions for gait planning. One is based on bionic principles and is more typically a motion control approach with a central pattern generator (CPG) (Yu et al., 2016). CPG-based robot control can achieve multi-modal gaits through a single network model (Zhang et al., 2021). Another type of control idea is model-based control. The best-known model is the spring-loaded inverted pendulum (SLIP) model, whose simplicity and effectiveness in modeling gait make it possible to better interpret walking and running gait and integrate them into a single model (Saar et al., 2017; Piovan and Byl, 2015). Current research on closed-chain linkage mobile robots has mainly focused on demonstrating the feasibility of mobility, with only minor coverage of their mobility capabilities and evaluation systems.

In this paper, a theoretical study of a planar 6R single-loop kinematic chain has been carried out, which is used as the basis for the mathematical modeling, kinematics analysis, and gait planning of a 4–5R rolling mechanism. A unified kinematic strategy expression, encapsulated in the form of the gait period table, is tailored for the kinematic chain's gait on the flat terrain. On this basis, three evaluation indicators are proposed: gait period, τ; drive effectiveness, η; and the volatility of CM, δ. By constraining these three evaluation indicators, different gaits can be proposed. Furthermore, by optimizing the corresponding indicators, two distinct gait patterns are achieved: a faster speed gait that prioritizes increased speed and a steady gait that emphasizes stability with reduced CM volatility. A novel theory concerning speed and steady gait has been introduced that is aimed at enhancing performance metrics when compared to the conventional gait.

The rest of the paper is organized as follows. The mechanism design and kinematic model are introduced in Sect. 2. The analyses of three gaits on flat ground are presented in Sect. 3. Sections 4 and 5 present the simulation and prototype experiments to test and verify the theoretical model, respectively. Section 6 provides a summary and outlook.

2 Mechanism design

2.1 Structure design

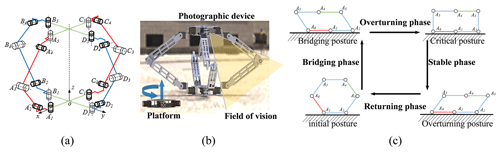
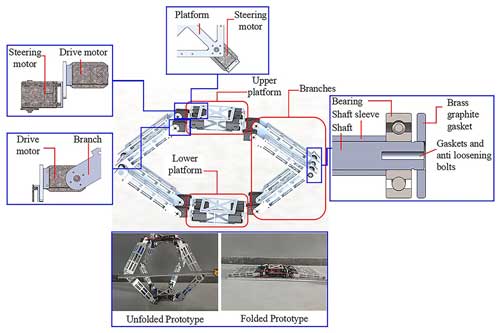
The sketch model of the 4–5R rolling mechanism is depicted in Fig. 1a. The mechanism comprises two identical platforms: the upper platform (A₅B₅C₅D₅) and the lower platform (A₁B₁C₁D₁) along with four symmetrical branches (A₂A₃A₄, B₂B₃B₄, C₂C₃C₄, and D₂D₃D₄) (Tian et al., 2017). The upper links (A₅C₅ and B₅D₅) and the lower links (A₁C₁ and B₁D₁) are constructed as diagonal lines of two identical platforms. The mechanism is equipped with a total of 20 revolute joints (R joints), consisting of 12 active R joints and 8 passive R joints.

Figure 1 The 4–5R rolling mechanism: (a) sketch model, (b) 3D model, and (c) one-step locomotion.

The 12 motors are strategically placed on each active joint to control the locomotion of the mechanism. The four branches are capable of rotating around the corners of the square platforms independently. During turning maneuvers, these branches execute coordinated rotations, facilitating the mechanism's change in direction. The parallel structure enables the platform to vertically and horizontally maneuver in working mode (Li et al., 2017), which extends its detection capabilities and adaptability to diverse environments as illustrated in Fig. 1b. Therefore, the mechanism has the prospect of using cameras as variant gimbals, suitable for use in ecological photography and topographic survey engineering.

The locomotion plane of the mechanism is analogous to a planar 6R single-loop kinematic chain, where a single step of locomotion involves at least four distinct phases and postures (Li et al., 2018) as shown in Fig. 1c. By considering the various stages and postures during locomotion, a variety of motion modes and gaits can be engineered to suit specific operational requirements.

2.2 Mathematical model

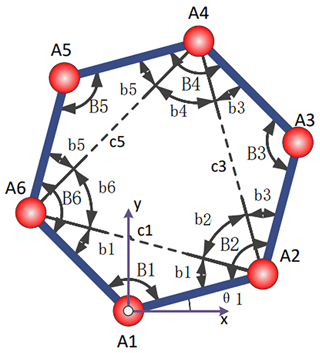
Based on the characteristics of the mechanism and locomotion, the kinematic model of the 4–5R rolling mechanism can be equivalent to the planar 6R single-loop kinematic chain. As shown in Fig. 2, vertex A₁ remains in contact with the ground during bridging and overturning process. Therefore, using A₁ as the origin establishes the kinematic analysis model of the mechanism. θ₁ is the angle between touchdown link A₆A₁ and the horizontal direction.

Figure 2 Planar 6R single-loop kinematic chain coordinate system.

Considering the unique attributes of its mechanism and movement, the kinematic model of the 4–5R rolling mechanism can be effectively equated to a planar 6R single-loop kinematic chain. As depicted in Fig. 2, vertex A₁ maintains continuous contact with the ground throughout the bridging and overturning procedures. Consequently, employing A₁ as the reference point for the origin establishes the kinematic analysis model of the mechanism. Here, θ₁ denotes the angle formed between the touchdown link A₆A₁ and the horizontal plane.

The plane hexagon possesses 3 degrees of freedom. Angles B₁, B₃, and B₅ serve as the driving parameters, pivotal in determining the positional coordinates of the vertices. The spatial coordinates of vertices A₁, A₂, A₃, A₄, A₅, and A₆ are articulated through the length, l, and the angles B₁, B₂, B₃, B₄, B₅, and B₆. The formulas of vertices are shown in Eq. (1).

$$\begin{array}{}\text{(1)}& \begin{array}{rl}{A}_{\mathrm{1}}=& (\mathrm{0},\mathrm{0}),\\ A_{\mathrm{2}}=& A_{\mathrm{1}}+l\left[-\cos \left(B_{\mathrm{1}}-{\mathit{\theta }}_{\mathrm{1}}\right)\sin \left(B_{\mathrm{1}}-{\mathit{\theta }}_{\mathrm{1}}\right)\right],\\ A_{\mathrm{3}}=& A_{\mathrm{2}}+l\left[\cos \left(B_{\mathrm{1}}+B_{\mathrm{2}}-{\mathit{\theta }}_{\mathrm{1}}\right)-\sin \left(B_{\mathrm{1}}+B_{\mathrm{2}}-{\mathit{\theta }}_{\mathrm{1}}\right)\right],\\ A_{\mathrm{4}}=& A_{\mathrm{3}}+l\left[-\cos \left(B_{\mathrm{1}}+B_{\mathrm{2}}+B_{\mathrm{3}}-{\mathit{\theta }}_{\mathrm{1}}\right)\right.\\ & \left.\sin \left(B_{\mathrm{1}}+B_{\mathrm{2}}+B_{\mathrm{3}}-{\mathit{\theta }}_{\mathrm{1}}\right)\right],\\ A_{\mathrm{5}}=& A_{\mathrm{4}}+l\left[\cos \left(B_{\mathrm{1}}+B_{\mathrm{2}}+B_{\mathrm{3}}+B_{\mathrm{4}}-{\mathit{\theta }}_{\mathrm{1}}\right)\right.\\ & \left.-\sin \left(B_{\mathrm{1}}+B_{\mathrm{2}}+B_{\mathrm{3}}+B_{\mathrm{4}}-{\mathit{\theta }}_{\mathrm{1}}\right)\right],\\ A_{\mathrm{6}}=& A_{\mathrm{5}}+l\left[-\cos \left(B_{\mathrm{1}}+B_{\mathrm{2}}+B_{\mathrm{3}}+B_{\mathrm{4}}+B_{\mathrm{5}}-{\mathit{\theta }}_{\mathrm{1}}\right)\right.\\ & \left.\sin \left(B_{\mathrm{1}}+B_{\mathrm{2}}+B_{\mathrm{3}}+B_{\mathrm{4}}+B_{\mathrm{5}}-{\mathit{\theta }}_{\mathrm{1}}\right)\right],\end{array}\end{array}$$

where

$$\begin{array}{}\text{(2)}& \left\{\begin{array}{l}{B}_{\mathrm{2}}=\mathit{\pi }-\frac{B_{\mathrm{1}}+B_{\mathrm{3}}}{\mathrm{2}}\\ +\arccos \frac{{\cos }^{\mathrm{2}}\left(\left(\mathit{\pi }-B_{\mathrm{1}}\right)/\mathrm{2}\right)+{\cos }^{\mathrm{2}}\left(\left(\mathit{\pi }-B_{\mathrm{3}}\right)/\mathrm{2}\right)-{\cos }^{\mathrm{2}}\left(\left(\mathit{\pi }-B_{\mathrm{5}}\right)/\mathrm{2}\right)}{\mathrm{2}\cos \left(\left(\mathit{\pi }-B_{\mathrm{1}}\right)/\mathrm{2}\right)\cos \left(\left(\mathit{\pi }-B_{\mathrm{3}}\right)/\mathrm{2}\right)},\\ B_{\mathrm{4}}=\mathit{\pi }-\frac{B_{\mathrm{3}}+B_{\mathrm{5}}}{\mathrm{2}}\\ +\arccos \frac{{\cos }^{\mathrm{2}}\left(\left(\mathit{\pi }-B_{\mathrm{3}}\right)/\mathrm{2}\right)+{\cos }^{\mathrm{2}}\left(\left(\mathit{\pi }-B_{\mathrm{5}}\right)/\mathrm{2}\right)-{\cos }^{\mathrm{2}}\left(\left(\mathit{\pi }-B_{\mathrm{1}}\right)/\mathrm{2}\right)}{\mathrm{2}\cos \left(\left(\mathit{\pi }-B_{\mathrm{3}}\right)/\mathrm{2}\right)\cos \left(\left(\mathit{\pi }-B_{\mathrm{5}}\right)/\mathrm{2}\right)},\\ B_{\mathrm{6}}=\mathit{\pi }-\frac{B_{\mathrm{5}}+B_{\mathrm{1}}}{\mathrm{2}}\\ +\arccos \frac{{\cos }^{\mathrm{2}}\left(\left(\mathit{\pi }-B_{\mathrm{1}}\right)/\mathrm{2}\right)+{\cos }^{\mathrm{2}}\left(\left(\mathit{\pi }-B_{\mathrm{5}}\right)/\mathrm{2}\right)-{\cos }^{\mathrm{2}}\left(\left(\mathit{\pi }-B_{\mathrm{3}}\right)/\mathrm{2}\right)}{\mathrm{2}\cos \left(\left(\mathit{\pi }-B_{\mathrm{1}}\right)/\mathrm{2}\right)\cos \left(\left(\mathit{\pi }-B_{\mathrm{5}}\right)/\mathrm{2}\right)},\end{array}\right.\end{array}$$

The plane 6R single-loop kinematic chain member is a homogeneous link of mass, m_li, and the vertex mass is m_Ai. By employing the closed-loop vector method, the CM of the mechanism, r_CM, can be articulated as in Eq. (3).

$$\begin{array}{}\text{(3)}& \left\{\begin{array}{ll}{r}_{\mathrm{CM}x}& =\frac{\sum _{i=\mathrm{1}}^{\mathrm{12}}{m}_i{r}_{ix}}{\sum _{i=\mathrm{1}}^{\mathrm{12}}{m}_i}\\ & =\frac{\mathrm{1}}{\sum _{i=\mathrm{1}}^{\mathrm{12}}{m}_i}\left(\sum _{i=\mathrm{1}}^{\mathrm{6}}{m}_{Ai}{A}_{ix}+\sum _{i=\mathrm{1}}^{\mathrm{6}}\frac{\mathrm{1}}{\mathrm{2}}{m}_{li}\left(A_{ix}+A_{(i+\mathrm{1})x}\right)\right),\\ & \\ r_{\mathrm{CM}y}& =\frac{\sum _{i=\mathrm{1}}^{\mathrm{12}}{m}_i{r}_{iy}}{\sum _{i=\mathrm{1}}^{\mathrm{12}}{m}_i}\\ & =\frac{\mathrm{1}}{\sum _{i=\mathrm{1}}^{\mathrm{12}}{m}_i}\left(\sum _{i=\mathrm{1}}^{\mathrm{6}}{m}_{Ai}{A}_{iy}+\sum _{i=\mathrm{1}}^{\mathrm{6}}\frac{\mathrm{1}}{\mathrm{2}}{m}_{li}\left(A_{iy}+A_{(i+\mathrm{1})y}\right)\right),\end{array}\right.\end{array}$$

Consequently, the interrelation between the CM coordinates and the driving angle can be deduced by integrating the aforementioned equations. This synthesis lays the groundwork for the formulation of mobile strategic expressions.

3 Gait analysis on flat ground

3.1 Evaluation indicators

The planar 6R single-loop kinematic chain, with its inherent multiple degrees of freedom, exhibits non-uniqueness in both its specific configurations and its transitional states. To streamline the comparison process, the following evaluation criteria have been established:

1. Gait period, τ. It is recognized that the velocity of the CM in a planar 6R single-loop kinematic chain is influenced by the maximum angular velocity attainable by the actuating joints and the chosen locomotion strategy. To facilitate a comparison among various gaits, we assume that the fastest angular velocity achievable at the driving angles for each gait is $\mathrm{1}\mathit{°}/t^{-\mathrm{1}}$, meaning that the minimum time required for a 1° change in the driving angles is 1t. Additionally, the gait period, denoted by τ, is defined as the number of time units necessary to complete one step of locomotion. Under identical conditions, a smaller τ indicates a higher average speed.

2. Drive effectiveness, η. It serves as a metric to quantify the efficacy with which the driving angles contribute to the locomotion process. This parameter is determined by the displacement in the x direction of the CM relative to a change in the driving angle. A positive value of η signifies that an increase in the driving angle propels the CM forward. The larger the value of η, the more significant the change in CM's position, thereby indicating a more effective locomotion.

   $$\begin{array}{}\text{(4)}& {\mathit{\eta }}_i={\displaystyle \frac{\partial r_{\mathrm{CM}x}}{\partial B_i}}\end{array}$$

3. The volatility of CM, δ. The concept of CM volatility, denoted by δ, is pivotal for assessing the smoothness of locomotion, closely tied to the one-step locomotion strategy previously discussed. This measure is articulated as a ratio: it compares the disparity between the maximum (r_CMy max) and minimum (r_CMy min) vertical displacements of the CM to the length (l) of the support link. A lower δ indicates a smoother locomotion pattern as it reflects less variation in CM's vertical movement.

   $$\begin{array}{}\text{(5)}& \mathit{\delta }={\displaystyle \frac{r_{\mathrm{CM}y}max-r_{\mathrm{CM}y}min}{l}}\times \mathrm{100}\mathit{\%}\end{array}$$

3.2 Locomotion strategy

The gait for the planar 6R single-loop kinematic chain is specifically tailored for operation on flat terrain. Assuming that the hexagonal link is lightweight and each vertex has a mass denoted as m_Ai, the position of the CM r_CM of the mechanism can be mathematically represented as in Eq. (6).

$$\begin{array}{}\text{(6)}& \left\{\begin{array}{l}{r}_{\mathrm{CM}x}=\frac{\sum _{i=\mathrm{1}}^{\mathrm{12}}{m}_i{r}_{ix}}{\sum _{i=\mathrm{1}}^{\mathrm{12}}{m}_i}=\frac{\mathrm{1}}{\mathrm{6}}p\\ \\ r_{\mathrm{CM}y}=\frac{\sum _{i=\mathrm{1}}^{\mathrm{12}}{m}_i{r}_{iy}}{\sum _{i=\mathrm{1}}^{\mathrm{12}}{m}_i}=\frac{\mathrm{1}}{\mathrm{6}}s\end{array}\right.\end{array}$$

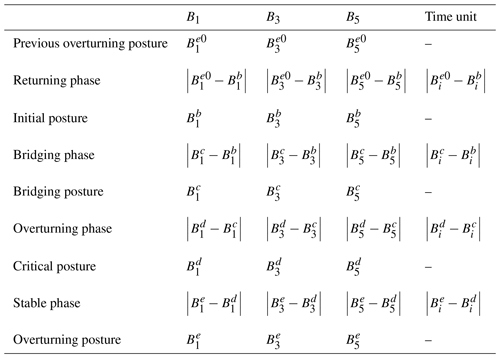
The gait periodic table serves as an overarching framework to delineate the gait patterns of the planar 6R single-loop kinematic chain, as detailed in Table 1. This comprehensive representation encapsulates the various locomotion strategies, providing a systematic overview of the chain's dynamic behavior.

Table 1 General gait periodic table.

Therefore, the gait period of the general gait can be obtained as follows:

$$\begin{array}{}\text{(7)}& \mathit{\tau }=\left|B_i^{e\mathrm{0}}-B_i^b\right|+\left|B_i^c-B_i^b\right|+\left|B_i^d-B_i^c\right|+\left|B_i^e-B_i^d\right|.\end{array}$$

3.3 Contrast gait

First, the contrast gait is introduced and the stages of the contrast gait are defined as follows:

• i.

  Returning phase. During this phase, the mechanism transitions from the previous overturning posture to the initial posture. In the initial posture, link A₆A₁ is in contact with the ground, while the angles at joints B₁, B₃, and B₅ are each set at 120°.

• ii.

  Bridging phase. In this phase, the link A₆A₁ maintains its position, while A₁A₂ rotates clockwise until it makes contact with the ground. Throughout this motion, the CM remains within the support area defined by the previous touchdown link. Upon reaching the bridging posture, the angles at joints B₁, B₃, and B₅ are adjusted to 180, 120, and 60°, respectively.

• iii.

  Overturning phase. During this phase, both links A₆A₁ and A₁A₂ execute a clockwise rotation until the CM of the mechanism transitions from the support area of A₆A₁ to the intersection of the support region between A₆A₁ and A₁A₂. At the critical posture, both links A₆A₁ and A₁A₂ are in contact with the ground, and the angles at joints B₁, B₃, and B₅ are precisely set to 180, 90, and 90°, respectively.

• iv.

  Stable phase. In this phase, links A₅A₆ and A₂A₃ perform a clockwise rotation, facilitating the forward locomotion of the CM into the support range of A₁A₂. During the stable phase, links A₆A₁ and A₁A₂ are in contact with the ground, with the angles at joints B₁, B₃, and B₅ set to 180, 60, and 120°, respectively.

The total duration of this phase is determined by the maximum number of time units required for the adjustment of each drive angle. Consequently, the gait period, τ, for the contrast gait is equivalent to the maximum number of time units necessary for the motion of each driving angle.

$$\begin{array}{}\text{(8)}& \mathit{\tau }=\mathrm{60}+\mathrm{60}+\mathrm{30}+\mathrm{30}=\mathrm{180}t\end{array}$$

The duration needed for the mechanism to complete a single step is equivalent to one gait period. Consequently, the average speed of the contrast gait is articulated in Eq. (9).

$$\begin{array}{}\text{(9)}& v_{\mathrm{contrast}}=l/\mathit{\tau }=l/\mathrm{180}t\end{array}$$

3.4 Speed gait

To enhance the speed of the planar 6R single-loop kinematic chain, it is imperative to minimize the gait period, τ. Referring to the general gait periodic table for flat terrain, the gait period, τ, is delineated in Eq. (10).

$$\begin{array}{}\text{(10)}& \mathit{\tau }=\left|B_i^{e\mathrm{0}}-B_i^b\right|+\left|B_i^c-B_i^b\right|+\mathrm{\Delta }{\mathit{\beta }}_{\mathrm{1}}+\mathrm{\Delta }{\mathit{\beta }}_{\mathrm{2}}\end{array}$$

When the initial posture is positioned at the path points between the overturning and bridging postures, the first two terms in Eq. (10) suggest that the number of time units required for the gait period, τ, is independent of the initial posture. Instead, it is contingent upon the cumulative number of units associated with the transition from the overturning to the bridging posture. To achieve the smallest possible gait period, τ, it is essential to identify the phase that minimizes the maximum value of the absolute differences in the drive angles, denoted as $max\mathit{\left\{}\right|\mathrm{\Delta }{B}_{\mathrm{1}}|,|\mathrm{\Delta }{B}_{\mathrm{3}}|,|\mathrm{\Delta }{B}_{\mathrm{5}}\left|\mathit{\right\}}$. Additionally, the changes in the drive angles, Δβ₁ and Δβ₂, should be as close to zero as feasible, albeit not exactly zero. Consequently, the equation becomes

$$\begin{array}{}\text{(11)}& \mathit{\tau }\approx \left|B_i^c-B_i^{be\mathrm{0}}\right|+\mathrm{\Delta }{\mathit{\beta }}_{\mathrm{1}}+\mathrm{\Delta }{\mathit{\beta }}_{\mathrm{2}}.\end{array}$$

Focusing exclusively on the scenario involving convex polygons, the permissible range of values for variables $B_{\mathrm{3}}^d$ and $B_{\mathrm{5}}^d$ in question is articulated in Eq. (12).

$$\begin{array}{}\text{(12)}& \mathit{\pi }/\mathrm{2}\le B_{\mathrm{3}}^d=B_{\mathrm{5}}^d<\mathit{\pi }\end{array}$$

A specific angle shares an identical profile with the subsequent angle in the clockwise sequence. However, its phase lags by one gait period. To maintain the number of time units at a minimum, the following condition applies:

$$\begin{array}{}\text{(13)}& \left\{\begin{array}{l}\mathrm{\Delta }{\mathit{\beta }}_{\mathrm{1}},\mathrm{\Delta }{\mathit{\beta }}_{\mathrm{2}}\to \mathrm{0},\\ B_{\mathrm{3}}^d=B_{\mathrm{5}}^d=\mathrm{90}\mathit{°}.\end{array}\right.\end{array}$$

By setting Δβ₁ and Δβ₂ to 2°, the speed gait periodic table can be derived. The initial posture is streamlined to an intermediate posture that lies between the overturning and bridging stages. The period for this speed gait is calculated to be 92t, which represents a reduction of 88t compared to the contrast gait. Consequently, the speed has increased by a factor of 1.96, indicating nearly double the improvement in velocity.

3.5 Steady gait

The stability of a gait is gauged by the volatility of the CM. This volatility is influenced by the length, l, and the disparity between the maximum vertical displacement, r_CMy max, and the minimum vertical displacement, r_CMy min, of the CM. Given that CM's movement is continuous throughout each phase, its value can be theoretically managed to oscillate between the initial and final states of a phase.

Drawing from the speed gait, a steady gait is engineered to mitigate CM volatility by managing the extremums encountered in each phase, thereby minimizing the minimum polarity. By adjusting the input angle profile and introducing a control node during the bridging phase, the minimum polarization is reduced, leading to more subdued CM fluctuations. The control node with angles (B₁  B₃  B₅) = (150°  150°  60°) is selected for this purpose.

Leveraging joint angles and contact information from each posture of the stabilised gait, the vertical displacement, r_CMy, for each phase and special posture within a single step of the steady gait can be ascertained. The minimum r_CMy value is found to be 49.9695 for the initial, bridging, and critical postures, while the maximum r_CMy value is 55.8057 for the initial posture and 50 for both bridging and critical postures. Consequently, the volatility of the CM during a stable gait is determined by Eq. (14).

$$\begin{array}{}\text{(14)}& \mathit{\delta }={\displaystyle \frac{r_{\mathrm{CM}y}max-r_{\mathrm{CM}y}min}{l}}\times \mathrm{100}\mathit{\%}=\mathrm{5.84}\mathit{\%}\end{array}$$

Employing the same set of equations and leveraging the parameter from both the constant gait and the speed gait, the calculated CM volatilities for these two gaits are found to be 43.30 % and 19.50 %, respectively. When compared with the 5.84 % volatility observed for the steady gait, the rationality and effectiveness of the steady gait design are substantiated.

4 The simulation analysis

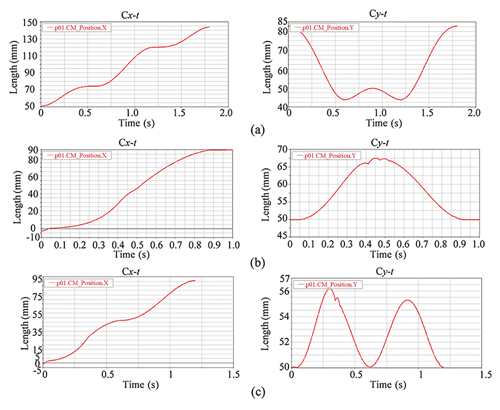
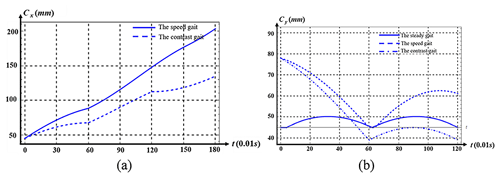
The contrast gait, speed gait, and steady gait processes have been simulated with the stipulation that 1t=0.01 s. This implies that the minimum time required to effect a 1° change in the drive angle is 0.01 s. The simulation curves for the horizontal (​​​​​​​Cx−t) and vertical (Cy−t) displacements over time for the contrast gait, speed gait, and steady gait are depicted in Fig. 3.

Figure 3 The simulation curve of (a) contrast gait, (b) speed gait, and (c) steady gait.​​​​​​​

The comparative analysis of speed between the speed gait and the contrast gait is illustrated in Fig. 4a, where the speed gait accomplishes a forward step in 0.92 s, representing a 95 % increase in speed relative to the contrast gait. The graphical representations of the CM fluctuations for the steady, speed, and contrast gaits are presented in Fig. 4b. The CM volatility for the contrast gait stands at 43.3 %, and for the speed gait, it is 19.5 %. The steady gait demonstrates a 37.46 % reduction in CM volatility in comparison to the contrast gait and a 13.66 % reduction when compared to the speed gait.

Figure 4 Comparison curve: (a) Cx and (b) Cy.

5 Prototype

In order to verify the correctness of each gait design, a physical prototype verification method was also adopted. The prototype was crafted with precise adherence to the proportional dimensions depicted in simulation model. As shown in Fig. 5, the physical sample is mainly composed of an upper platform, a lower platform, and multiple branches connecting the two platforms. Both platforms are square, each corner of which is linked to a steering motor, facilitating directional adjustments of the branches and the overall steering capability of the mechanism. On this basis, the steering motors and the branches are connected by drive motors, achieving changes in the overall shape and mobility of the mechanism. The branch is divided into two parts, with two parts joined by a shaft rotation. To ensure smooth operation, components like shaft sleeves, bearings, and gaskets are integrated, promoting lubrication between the segments. This meticulous design approach guarantees the mechanical integrity and performance of the prototype.

Figure 5 Prototype.

Furthermore, Fig. 5 provides a detailed view of the prototype's design dimensions in two distinct configurations. In its unfolded state, the prototype spans a generous 550 mm by 550 mm by 600 mm, offering ample space for movement and operation. Conversely, when the prototype is compactly folded, its dimensions are a more manageable 950 mm by 240 mm by 110 mm, making it easy to transport and store.

This ingenious design not only allows for flexibility in use but also ensures that the prototype remains portable despite its functional complexity. The total mass of the prototype, which is a critical factor in its practical application, is meticulously measured and recorded at 7.30 kg. This weight is a testament to the balance between the prototype's robust construction and the need for it to be easily handled and maneuverable in various environments.

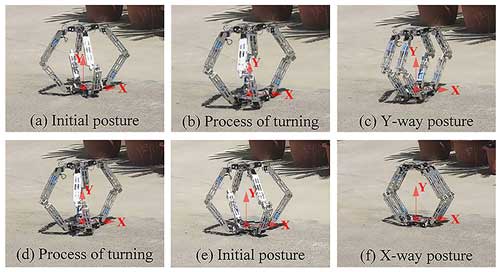
The video of the prototype is shown in the Supplement. The prototype is capable of transitioning from the initial posture to either the X-way or Y-way posture and can also make a direct transition from one posture to another. Figure 6a–c illustrate the prototype's progression from the initial posture to the Y-way posture, while Fig. 6d–f demonstrate the shift from the Y-way posture to the X-way posture. In the event of a recovery step, the prototype can revert to the initial posture from any of the intermediate postures.

Figure 6 The steering processes of the prototype.

Figure 7 illustrates the experimental progression of the prototype advancing forward by 1000 mm using the contrast gait, speed gait, and steady gait. In this scenario, by executing three forward steps within a single period, the prototype achieves a movement speed of 0.1 m s⁻¹ for the contrast gait, 0.25 m s⁻¹ for the speed gait, and 0.125 m s⁻¹ for the steady gait.

Figure 7 Prototype experiments: (a) contrast gait, (b) speed gait, and (c) steady gait.

6 Conclusion

A novel 4–5R rolling mechanism, derived from a planar 6R single-loop kinematic chain, has been introduced. This mechanism leverages the integration and interconnection of multiple planar mechanisms to facilitate spatial steering capabilities. A comprehensive locomotion strategy suitable for flat ground has been proposed, and through the analysis of the contrast gait, key parameters such as speed and CM volatility have been determined. Subsequently, a faster speed gait and a more stable gait with reduced CM volatility have been successfully optimized. In conclusion, a prototype with spatial steering functionality has been designed, grounded in the aforementioned theories, and prototype experiments have been conducted to substantiate the validity of these concepts.

Looking ahead, future enhancements to the mechanism are slated in three key areas. Firstly, the optimization of collision forces during rolling locomotion will be addressed. Secondly, the analysis of the obstacle-crossing process will be expanded upon, utilizing the established locomotion strategy. Thirdly, the redesign of link shapes within the mechanism will be tailored to better suit specific application environments.