the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Multi-objective optimization design of parallel manipulators using a neural network and principal component analysis
Chao Yang
Peijiao Li
Yang Wang
Wei Ye
Tianze Sun
Fengli Huang
Hui Zhang
In this work, a multi-objective optimization design method is proposed based on principal component analysis (PCA) and a neural network to obtain a mechanism's optimal comprehensive performance. First, multi-objective optimization mathematical modeling, including design parameters, objective functions, and constraint functions, is established. Second, the sample data are obtained through the design of the experiment (DOE) and are then standardized to eliminate the adverse effects of a non-uniform dimension of objective functions. Third, the first k principal components are established for p performance indices (k<p) using the variance-based PCA method, and then the factor analysis method is employed to define its physical meaning. Fourth, the overall comprehensive performance evaluation index is established by objectively determining weight factors. Finally, the computational cost of the modeling is improved by combining the neural network and a particle swarm optimization (PSO) algorithm. Dimensional synthesis of a Sprint (3RPS) parallel manipulator (PM) is taken as a case study to implement the proposed method, and the optimization results are verified by a comprehensive performance comparison of robots before and after optimization.
- Article
(2912 KB) - Full-text XML
- BibTeX
- EndNote
Parallel manipulators (PMs) have become a research hotspot because of their excellent dynamic performance, simple inverse kinematics, and high stiffness (Yang et al., 2022). Sprint (3PRS) (Chen et al., 2014), Tricept (3UPS-UP) (Farooq et al., 2021), and delta (Wang et al., 2014) robots have been successfully commercialized, and the 3RPS PM is used as a parallel module in the five-axis machining center for blade surface machining (Arabshahi and Novinzadeh, 2015). Comprehensive performance of PMs is crucial for machining precision. Therefore, multi-objective optimization is necessary to achieve optimal comprehensive performance.
PMs have smaller workspaces compared with serial robots. Therefore, maximizing the workspace volume, especially the regular workspace volume, is a major task of a PM's optimization design (Yang et al., 2019). However, poor performance, e.g., kinematic, stiffness, and dynamic performance, may be caused while the workspace volume is maximized (Shi et al., 2014). This problem can be fixed by considering other performance indices as constraint functions or by carrying out a multi-objective optimization design.
Compared with kinematic analysis, dynamic analysis is more complicated because the overall stiffness and mass matrices are difficult to describe due to the multiple closed-loop characteristics of PMs (Shi et al., 2014). Limited discrete-node function values in the workspace are adopted to evaluate the objective performance (global performance index, GPI) due to the difficulty in obtaining its analytical expressions in the workspace. It significantly increases the performance index evaluation's computational cost (Lian et al., 2017). Therefore, effective multi-objective optimization design is challenging.
Since multiple performance indices are often presented as competitive coupling relations, this makes it difficult to obtain an optimal solution with a definite physical meaning. The comprehensive objective method is most commonly used to fix this problem, and it defines the weighted sum of objective functions as a comprehensive index (Wang and Zhang, 2017; Zhang and Nelson, 2011). Xu et al. (2017) optimized the hybrid mechanism's comprehensive performance through a comprehensive objective method wherein the workspace volume and stiffness performance were considered as objective functions. Huang et al. (2018) adopted this method to optimize reconfigurable a PM's workspace volume, global dexterity, and stiffness indices. Various combinations of weighting factors are provided to decision-makers. However, the weight coefficients in this method are often determined artificially, and the dimension and unit of the objective function are inconsistent, which leads to the limitation of the application of this method (Fan et al., 2022).
Yang et al. (2019) derived a globally optimal comprehensive performance by proposing a multi-objective optimization game algorithm. Globally optimal solutions are derived based on their weight factors rather than an objective function weight sum. The method is simple but needs to manually set the weight factors and calculate the objective function's values at each discrete node in advance. Discrete node density decides the precision. As the density of discrete nodes increases, the calculation cost increases exponentially. For instance, for a PM with 3 degrees of freedom (DOFs), a population np, and generations ng, if the node density in the workspace is increased to 2 times that of the original, the computational cost will be npng23 times that of the original (Yang et al., 2019; Wu, 2017).
The Pareto front method has become a research hotspot of multi-objective optimal design methods because it can obtain multiple sets of non-dominated solutions (Altuzarra et al., 2011; Ling et al., 2022). Cui et al. (2015) combined a genetic algorithm (GA) and insight software to optimize the kinematics and kinetic flexibility of the tunnel tube assembly system's 3-DOF PMs and obtained multiple sets of non-dominated solutions. Qi et al. (2018), Sun and Lian (2018), and Sun et al. (2019) defined the sum of minimum squares (i.e., the cooperative balance point) from the non-dominated solutions as the global optimal solution. However, the physical explanation for this method is not clearly defined.
Establishing workspaces' analytic formulas is challenging, especially for regular workspaces, so the GPIs often obtained in terms of numerical methods include the Monte Carlo method (Wang et al., 2015) and the discrete-node method (Xu et al., 2018). High computational costs greatly reduce the optimized design's computational efficiency. The response surface model (RSM), including a back-propagation (BP) neural network (Zhang and Gao, 2008; Gao et al., 2010), multivariate regression (Yang et al., 2022; Lian et al., 2019), and Gaussian regression (Vinh et al., 2019), is often used to fix this problem, wherein the BP neural network has attracted extensive attention due to its strong learning and nonlinear fitting capabilities. Therefore, the BP neural network model is adopted to establish the RSM of the GPIs and the design parameters in this work.
The main contribution of this work is to propose a multi-objective optimization design method in terms of factor analysis, BP neural network, principal component analysis (PCA), and particle swarm optimization (PSO) algorithm (Sun and Lian, 2018; Wang et al., 2017) to achieve the optimal comprehensive performance of the mechanism. The proposed method has a clear physical explanation and a low computational expense.
The remainder of the work is arranged as follows. The structure description of the 3RPS PM is presented in Sect. 2. Objective functions of the 3RPS PM are presented in Sect. 3. The multi-objective optimization design of the 3RPS PM is introduced in Sect. 4, and the optimization results are discussed in detail. Finally, conclusions are drawn in Sect. 5.
The basic idea of the multi-objective optimization design for the PMs proposed in this work is to first use PCA to construct an overall comprehensive performance evaluation index with objectively determined weight factors and clear physical significance. Then a response surface model between objective functions and design parameters is constructed based on a neural network to solve the problem of the high computational cost of the objective functions in the workspace. Figure 1 shows the procedure of the proposed multi-objective optimization design method of PMs based on a neural network and PCA. The steps are described as follows.
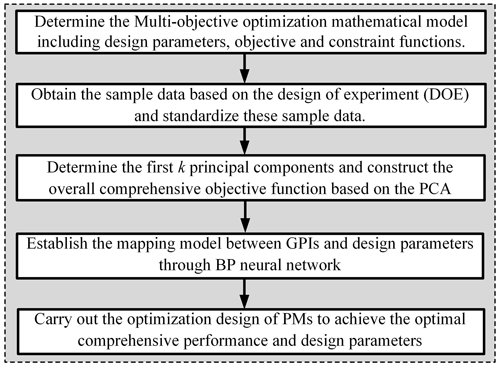
Figure 1Procedure of the multi-objective optimization design method of PMs based on the neural network and PCA.
Step 1. Establish the multi-objective optimization mathematical model, including design parameters, objective functions, and constraint functions, wherein the limitations of the design parameters, actuation lengths, and joint angles should be given.
Step 2. Obtain the sample data based on the design of the experiment: Latin hypercube sampling (LHS) is recommended in this work, and then it is necessary to standardize the original sample data to eliminate adverse influences caused by non-uniform dimensions of objective functions. The Z-score method is adopted in this work.
Step 3. Establish the correlation matrix of multiple performance indices and the first k principal components according to the cumulative contribution rate (the ratio of the sum of the first k eigenvalues of the correlation matrix to the sum of all the eigenvalues). The i principal components can be established based on the corresponding eigenvectors of the correlation matrix. Finally, the overall comprehensive performance index is defined as the sum of the product of the first k eigenvalues and the corresponding principal components.
Step 4. Establish the RSM between GPIs and design parameters based on the neural network to avoid the high computational cost of the objective functions in the workspace.
Step 5. Combine the overall comprehensive performance index and RSMs to carry out the optimization design of PMs to achieve optimal design parameters with a clear physical explanation.
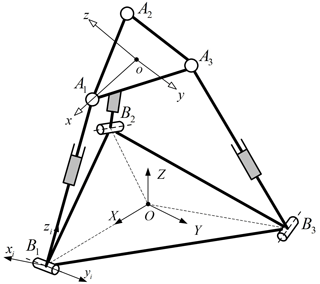
Figure 2 shows a spatial 3RPS PM with 3 DOFs. Three identical branches connect the base and mobile platform at points Bi and Ai with revolute joints and spherical joints, respectively. An upper rod and a lower rod connected by a prismatic joint constitute limbs. Inputs to the mechanism refer to the three prismatic joints. Coordinate frames , , and are attached to the limb, moving platform, and base, respectively (see Fig. 2). Both ΔA1A2A3 and ΔB1B2B3 are equilateral triangles with and . Each of the revolute joint axes is perpendicular to vector OBi and lies on the X–Y plane. Geometric and physical parameters before optimization are given as moving platform height h=0.05 m, r1=1.7 m, elasticity modulus E=200 GPa, r2=0.8 m, shear modulus G=77 GPa, and di=0.4 m (diameter of the link). The 3RPS PM's multi-objective optimization aims to select appropriate r1 and r2 values to achieve maximal comprehensive performance.
The 3RPS PM is to be used as the parallel module of the high-speed machining equipment, wherein dynamic performance, motion or force transmission performance, and operation workspaces strongly influence the mechanism's comprehensive performance. Therefore, the regular workspace volume, kinematic performance, and natural frequency are considered the three objective functions in this paper.
4.1 Workspace evaluation
A PM's workspace is smaller than those of serial mechanisms. Thus, PM optimization should primarily maximize workspace volume. A regular workspace volume (Yang et al., 2019) is recommended as the workspace evaluation index due to some performance indices being poor at the boundary of the reachable workspace, and the reachable workspace does not apply to trajectory planning (Babu et al., 2016). The method proposed in Yang et al. (2019) is adopted to calculate the regular workspace volume, the reachable workspace is first classified into n layers with an equal interval height of dz, and then the inscribed circle of the workspace boundary in each layer is calculated. The 3RPS PM's regular workspace volume is expressed as follows:
where is the inscribed circle's area in the ith layer. ρi is the radius. The minimum radius of inscribed circles is set to 50 mm in the work to guarantee the necessary operation workspace of the 3RPS PM.
4.2 Kinematic performance evaluation
The kinematic condition number is often adopted as the kinematic index of PMs to measure their dexterity, manipulability, and singularity. The main limitation of the condition number index is the non-uniform dimension of the Jacobian matrix for the PMs with mixed DOFs. Characteristic length is often adopted to fix this problem. However, due to the subjectivity of characteristic length selection and the fact that only some elements of the Jacobian matrix are involved in characteristic length calculation, the physical explanation for the characteristic length is ambiguous (Zang et al., 2019; Wang et al., 2019). The motion or force transmission index (Wu et al., 2023; Liu et al., 2012) is recommended in this paper due to its advantages of being frame-free and dimensionless.
The ith limb's twist system is derived through screw theory:
where Sij is the jth twist of the ith limb, li is the unit vector along the vector BiAi. Ri represents a rotation matrix from limb coordinate frame {Bi} to global coordinate frame {O}. ei in Eq. (2) is presented in , , and .
The transmission wrench of the ith limb can be obtained based on its reciprocal product with the twist (Sij) of the passive joints being zero:
The ith limb's input twist screw is
All of the inputs except the one in the ith limb are locked to derive the instantaneous 1-DOF output twist screw SOi:
where Ui is the mechanism's constraint wrench system.
Accordingly, the ith limb's transmission and input indices are expressed as follows:
Both of the output and input indices are considered to obtain the local transmission index (LTI):
The global transmission index (GTI) is obtained to determine the global kinematic performance in a PM's regular workspace:
where N is the number of discrete grid nodes in the prescribed workspace.
4.3 Dynamic performance evaluation
The natural frequency is the frequency at which a system tends to oscillate in the absence of external forces or damping. The first natural frequency, i.e., the fundamental frequency (Ganesh and Rao, 2020), is recommended in this paper due to its comprehensive consideration of the stiffness, mass, and damping of PMs.
The global independent generalized displacement coordinates (IGDCs) (Yang et al., 2021) are recommended as the elastodynamic modeling method of PMs in this paper due to the Lagrangian multipliers and kinematic constraint equations not being required.
The ith link's elastodynamic equation expressed in the limb coordinate frames is given as follows considering that the link is discretized into one element (the number of elements has little influence on the calculation accuracy of the fundamental frequency; Yang et al., 2021):
where is the ith link's displacement column vector. LdBi(LφBi) is point Bi's linear displacement coordinate. LdAi(LφAi) is point Ai's angular displacement coordinate. , and LfBi(LmBi) and LfAi(LmAi) are the forces (moments) exerted on points Bi and Ai, respectively. Ke is the element stiffness matrix. Me is the element mass matrix. L in the upper-left corner indicates that the vector is expressed in the local frame system.
Equation (9) can be further presented in the global coordinate system:
where , , and Fi=Tifi. .
With a rigid assumption of the moving platform, its elastodynamic equation in the global coordinate system is
where . and R is the rotation matrix from frames {o} to {O}. LMp is the moving platform's mass matrix. , dp, and φp, respectively, denote point o's linear and angular displacement coordinates in the global coordinate frame. , and mp and fp are the moment and force, respectively, exerted on the moving platform.
The moving platform and link BiAi are connected at point Ai through a spherical joint. The compatibility equation between point o's displacement coordinates and point Ai's linear displacement coordinates of the ith link can be obtained according to multipoint constraint (MPC) theory (Yang et al., 2019).
Revolute joints are used to connect the base to link BiAi based on MPC theory. The boundary conditions in the local coordinate frame are as follows:
where and are point Bi's angular displacement coordinates along the xi and zi axes, respectively.
Boundary conditions in Eq. (13) can be further expressed based on Ganesh and Rao (2020).
Accordingly, the global IGDC of the manipulator can be extracted as follows.
Finally, the elastodynamic control equation of the 3RPS PM is given by
where , , , Ui=NiU, Ni is the mapping matrix from the generalized displacement coordinate Ui to the global IGDC U.
It can be seen that the Lagrangian multipliers or the simultaneous kinematic constraint equations are not required in Eq. (16): all the kinematic constraints of the mechanism were considered in the global IGDC and the mapping matrix Ni, which is beneficial for solving dynamic equations.
The angular frequency in radian per second is derived by
The fundamental frequency is
The PM's global dynamic index is
The multi-objective optimization mathematical modeling of the 3RPS PM (Babu et al., 2013) is
where m and m. Li is link BiAi's length. φi and θi represent angles among the moving platform, base, and link, respectively, and ∘.
The PCA recombines the m dependent original indices into a new set of p (p<m) independent principal components (Fi) and determines an overall comprehensive index with a deterministic weight factor based on the variance-based method, which satisfies . The physical meanings of the principal components are then explained by using the factor analysis method.
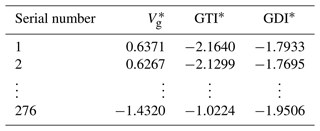
Consider the non-uniform dimensions of objective functions: it is necessary to convert original sample data to the standardized X* before calculating the principal components. The Z-score method is adopted here.
where , , and , μj=E(Xj).
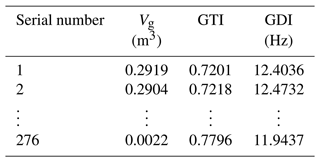
Population characteristics are often represented by sample data in terms of the LHS method (Lian et al., 2017). Table 1 shows 276 sets of sample data designed based on the LHS method. Objective functions' standardized sample data of the 3RPS PM are presented through Eq. (21) (see Table 2). The correlation matrix R is established to reflect correlations of objective functions:
where .
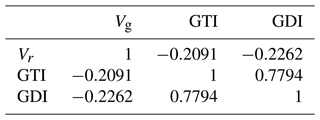
The correlation matrix can be defined in Eq. (23) for standardized data X* as follows:
The correlation matrix of the objective functions obtained by Eq. (23) is shown in Table 3. Dynamic performance and motion or force transmission performance are negatively correlated with the workspace volume. Dynamic performance and kinematic performance present positive correlations, which is consistent with the results in Chen and Yang (2021).
The first k principal components' cumulative contribution rate and the ith principal component are defined by
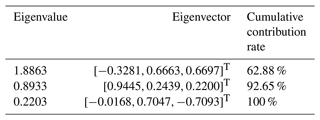
where λi and are the ith eigenvalue and eigenvector of the correlation matrix, respectively. δ is the first k principal components' cumulative contribution rate.
The first two eigenvalues' cumulative contribution rate is 92.65 %, which is greater than 85 % (Kuroda et al., 2011) (see Table 4). Objection function information is included in the first two principal components (see Eq. 25).
The physical explanation of principal components is given by introducing the factor analysis method. The factor-loading matrix is first given by
The factor-loading matrix should be further simplified to explain principal components until each objective function has a large loading in only one principal component. The maximum orthogonal rotation method of square differences is usually adopted (Mardian et al., 1979):
where Ω is the orthogonal matrix.
Table 4Principal component cumulative contribution rate and correlation matrix eigenvalues and eigenvectors.
Repeat Eq. (28) until the allowable error is larger than the change in B's relative variances.
The kinematic performance and the dynamic performance have larger factor loadings for the first principal component (see Table 5). Therefore, the kinematic and dynamic performance factor is named for the first principal component and presents a PM's dynamic performance and kinematic performance. The workspace volume has a larger factor loading on the second principal component; thus, the workspace factor is named for the second principal component, which reflects the mechanism's workspace volume. So far, the physical explanation of the principal components has been fully defined through the factor analysis method.
Accordingly, the 3RPS PM's overall comprehensive performance evaluation index is
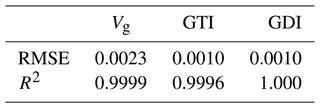
Generally, the GPI is obtained by calculating the variance or mean of the function value of nodes in the regular workspace. Computational costs increase exponentially with increased discrete points. The high computational intensity reduces the optimization design efficiency. The RSM between design parameters and GPIs is established using the BP neural network in this work to improve the computational intensity for its powerful nonlinear fitting effect. The BP neural network's hidden layer sizes are set to 30. The recommended acceptance levels of RMSE and R2 in Agarwal and Renaud (2004) are below 0.2 and above 0.9, respectively. Table 6 shows the optimal accuracy assessment for the BP-based mapping model through five tests that verify the accuracy and effectiveness of the BP-based RSM.
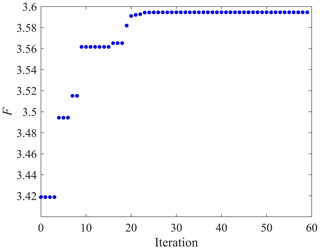
The population- and evolution-based PSO intelligence algorithm determines their search directions based on their velocities and replaces the GA's mutation and crossover. The PSO algorithm's convergence efficiency was proven in Wang et al. (2017). Thus, the PSO algorithm is used in this work. Table 7 shows the PSO algorithm's setting that is recommended in Sun et al. (2018). The 59 iterations are performed to converge the objective function to 3.5945, and the optimal design parameters are r1=1.4340 and r2=1.0660 (see Fig. 3). The calculation time of the proposed algorithm is 192 s on a computer 3.00 GHz CPU, while the PSO algorithm is 6285 s and 96.94 % of the computational cost is saved. Optimized dynamic performance, kinematic performance, and workspace volume increase by 44.57 %, 6.74 %, and 283.69 %, respectively; after optimization, the overall comprehensive index F increases by 118.92 % (see Table 8). The multi-objective optimization design results verified the effectiveness of the proposed method.
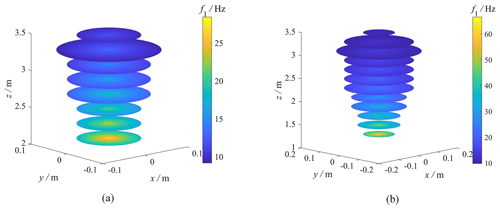
Dynamic performance, kinematic performance, and regular workspace have been enhanced as shown in Table 8. The distributions of the performance indices are shown in Figs. 4–5, the maximum radius of the workspace has been increased from 0.096 to 0.156 m, the maximum LTI has been increased from 0.95 to 0.99, and the maximum first natural frequency has been increased from 28.42 to 66.57 Hz, which is consistent with the results in Table 8. It is worth noting that, since the mechanism has a relatively excellent kinematic performance before optimization, the kinematic performance has not been significantly improved after optimization.
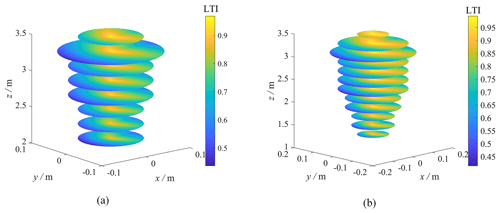
Figure 4Distribution of the LTI in the regular workspace. (a) Before optimization. (b) After optimization.
The results of multi-objective optimization design significantly affect the comprehensive performance of PMs. Obtaining the mechanism's optimal comprehensive performance with clear physical significance is challenging because of weight factors' subjectivity and multiple performance indices' non-uniform dimensions. Meanwhile, the high computational costs of the GPI undermine PMs' multi-objective optimization design efficiency. In this paper, the multi-objective optimization design method based on the PCA, factor analysis, PSO algorithm, and neural network was proposed to fix these problems, and the multi-objective optimization of the 3RPS PM was taken as a case study to implement the proposed method.
Considering the fundamental frequency, the motion or force transmission performance, and the regular workspace volume of the 3RPS PM to be objective functions, the results of PCA and factor analysis showed that the first principal component reflected the mechanism's dynamic and kinematic performances. The second one reflected the mechanism's regular workspace volume. The computational cost of the proposed approach was reduced by 96.95 % compared with the PSO algorithm. Meanwhile, the mechanism's overall comprehensive performance increased by 118.92 %, and the dynamic performance, kinematic performance, and workspace volume increased by 44.57 %, 6.74 %, and 283.69 %, respectively.
Although neural networks have a strong fitting ability, they have not revealed the inherent mechanism between the objective functions and the design parameters. In our future work, we will study the analytical formula between the objective function and the design parameters.
The corresponding author can provide MATLAB and Ansys files to support the work.
Conceptualization: CY and HZ; methodology: WY and FH; software: TS and YW; validation: PL and YW; formal analysis: CY and HZ; investigation: PL and CY; resources: HZ; writing – original draft preparation: TS and CY; writing – review and editing: CY and HZ; visualization: YW and CY; supervision: HZ; project administration: HZ; funding acquisition: WY and HZ.
The contact author has declared that none of the authors has any competing interests.
Publisher’s note: Copernicus Publications remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This study was funded by the National Natural Science Foundation of China (NSFC) (grant no. 51705465) and the Public Welfare Research Project of Jiaxing, Zhejiang Province, China (grant no. 2023AY11007).
This paper was edited by Zi Bin and reviewed by three anonymous referees.
Agarwal, H. and Renaud, J.: Reliability based design optimization using response surfaces in application to multidisciplinary systems, Eng. Optimiz., 36, 291–311, 2004.
Altuzarra, O., Pinto, C., Sandru, B., and Hernandez, A.: Optimal dimensioning for parallel manipulators: workspace, dexterity, and energy, J. Mech. Design, 133, 041007, https://doi.org/10.1115/1.4003879, 2011.
Arabshahi, H. Z. and Novinzadeh, A. B.: Comparison of motion control techniques for a 3RPS parallel manipulator, in: Proceedings of the 2015 3rd RSI International Conference on Robotics and Mechatronics (ICROM), Tehran, Iran, 7–9 October 2015, IEEE, 302–307, https://doi.org/10.1109/ICRoM.2015.7367801, 2015.
Babu, S. R., Raju, V. R., and Ramji, K.: Design for optimal performance of 3-RPS parallel manipulator using evolutionary algorithms, T. Can. Soc. Mech. Eng., 37, 135–160, https://doi.org/10.1139/tcsme-2013-0009, 2013.
Babu, S. R., Raju, V. R., and Ramji, K.: Design optimization of 3PRS parallel manipulator using global performance indices, J. Mech. Sci. Technol., 30, 4325–4335, https://doi.org/10.1007/s12206-016-0847-5, 2016.
Chen, Q. and Yang, C.: Hybrid algorithm for multi-objective optimization design of parallel manipulators, Appl. Math. Model., 98, 245–265, https://doi.org/10.1016/j.apm.2021.05.009, 2021.
Chen, X., Liu, X.-J., Xie, F. G., and Sun, T.: A comparison study on motion/force transmissibility of two typical 3-dof parallel manipulators: the sprint Z3 and A3 tool heads, Int. J. Adv. Robot. Syst., 11, 1–10, https://doi.org/10.5772/57458, 2014.
Cui, G., Zhang, D., Zhou, H., and Zhang, Y. W.: Operating dexterity optimization and analysis of a 3-DOF parallel manipulator for a tunnel segment assembly system, Int. J. Mech. Mater. Des., 11, 277–285, https://doi.org/10.1007/s10999-014-9268-8, 2015.
Fan, W., Xu, Z., Wu, B., He, Y. S., and Zhang, Z. F.: Structural multi-objective topology optimization and application based on the criteria importance through intercriteria correlation method, Eng. Optimiz., 54, 830–846, https://doi.org/10.1080/0305215X.2021.1901087, 2022.
Farooq, S. S., Baqai, A. A., and Shah, M. F.: Optimal design of tricept parallel manipulator with particle swarm optimization using performance parameters, J. Eng. Res., 9, 378–395, https://doi.org/10.36909/jer.v9i2.9073, 2021.
Ganesh, S. S. and Rao, A. B. K.: Design optimization of a 2-DOF parallel kinematic machine based on natural frequency, J. Mech. Sci. Technol., 34, 835–841, https://doi.org/10.1007/s12206-020-0133-4, 2020.
Gao, Z., Zhang, D., and Ge, Y.: Design optimization of a spatial six degree-of-freedom parallel manipulator based on artificial intelligence approaches, Robot. Cim-Int. Manuf., 26, 180–189, https://doi.org/10.1016/j.rcim.2009.07.002, 2010.
Huang, G., Guo, S., Zhang, D., Qu, H. B., and Tang, H. Y.: Kinematic analysis and multi-objective optimization of a new reconfigurable parallel mechanism with high stiffness, Robotica, 36, 187–203, https://doi.org/10.1017/S0263574717000236, 2018.
Kuroda, M., Mori, Y., Iizuka, M., and Sakakihara, M.: Acceleration of the alternating least squares algorithm for principal components analysis, Comput. Stat. Data An., 55, 143–153, https://doi.org/10.1016/j.csda.2010.06.001, 2011.
Lian, B., Wang, X. V., and Wang, L.: Static and dynamic optimization of a pose adjusting mechanism considering parameter changes during construction, Robot. Cim-Int. Manuf., 59, 267–277, https://doi.org/10.1016/j.rcim.2019.04.008, 2019.
Lian, B. B., Sun, T., and Song, Y. M.: Parameter sensitivity analysis of a 5-DoF parallel manipulator, Robot. Cim.-Int. Manuf., 46, 1–14, https://doi.org/10.1016/j.rcim.2016.11.001, 2017.
Ling, M., Song, D., Zhang, X., He, X., Li, H., Wu, M. X., Cao, L., and Lu, S. L.: Analysis and design of spatial compliant mechanisms using a 3-D dynamic stiffness model, Mech. Mach. Theory, 168, 104581, https://doi.org/10.1016/j.mechmachtheory.2021.104581, 2022.
Liu, X.-J., Wu, C., and Wang, J. S.: A new approach for singularity analysis and closeness measurement to singularities of parallel manipulators, J. Mech. Robot., 4, 041001, https://doi.org/10.1115/1.4007004, 2012.
Mardian, K. V., Kent, J. T., and Bibby, J. M.: Multivariate analysis, Academic Press, New York, https://doi.org/10.2307/3617970, 1979.
Qi, Y., Sun, T., and Song, Y.: Multi-objective optimization of parallel tracking mechanism considering parameter uncertainty, J. Mech. Robot., 10, 041006, https://doi.org/10.1115/1.4039771, 2018.
Shi, H., Duan, X., and Su, H.-J.: Optimization of the workspace of a mems hexapod nanopositioner using an adaptive genetic algorithm, in: Proceedings of the 2014 IEEE International Conference on Robotics and Automation (ICRA), Hong Kong, China, 1 May 2014–7 June 2014, IEEE, 4043–4048, https://doi.org/10.1109/ICRA.2014.6907446, 2014.
Sun, T. and Lian, B. B.: Stiffness and mass optimization of parallel kinematic machine, Mech. Mach. Theory, 120, 73–88, https://doi.org/10.1016/j.mechmachtheory.2017.09.014, 2018.
Sun, T., Lian, B., Song, Y., and Feng, L.: Elastodynamic optimization of a 5-DoF parallel kinematic machine considering parameter uncertainty, IEEE-ASME T. Mech., 24, 315–325, https://doi.org/10.1109/TMECH.2019.2891355, 2019.
Vinh, N., Cvitanic, T., and Melkote, S.: Data-driven modeling of the modal properties of a six-degrees-of-freedom industrial robot and its application to robotic milling, J. Manuf. Sci. E.-T. ASME, 141, 121006, https://doi.org/10.1115/1.4045175, 2019.
Wang, H., Zhang, L. S., Chen, G. L., and Huang, S. Z.: Parameter optimization of heavy-load parallel manipulator by introducing stiffness distribution evaluation index, Mech. Mach. Theory, 108, 244–259, https://doi.org/10.1016/j.mechmachtheory.2016.10.011, 2017.
Wang, R. and Zhang, X.: Optimal design of a planar parallel 3-DOF nanopositioner with multi-objective, Mech. Mach. Theory, 112, 61–83, https://doi.org/10.1016/j.mechmachtheory.2017.02.005, 2017.
Wang, S.-T., Cheng, G., Yang, D.-H., and Yang, J. H.: Unified kinematics analysis and low-velocity driving optimization for parallel hip joint manipulator, J. Mech. Design, 137, 082301, https://doi.org/10.1115/1.4030433, 2015.
Wang, W. J., Yu, L. T., Zhang, B. Y., and Tao, W.: The new method of static modeling and simlink simulation for delta parallel mechanism, in: Proceedings of the 2014 IEEE International Conference on Mechatronics and Automation (ICMA), Tianjin, China, 3–6 August 2014, IEEE, 680–685, https://doi.org/10.1109/ICMA.2014.6885779, 2014.
Wang, Y. J., Belzile, B., Angeles, J., and Li, Q. C.: Kinematic analysis and optimum design of a novel 2PUR-2RPU parallel robot, Mech. Mach. Theory, 139, 407–423, https://doi.org/10.1016/j.mechmachtheory.2019.05.008, 2019.
Wu, G.: Optimal structural design of a Biglide parallel drill grinder, Int. J. Adv. Manuf. Tech., 90, 2979–2990, https://doi.org/10.1007/s00170-016-9625-x, 2017.
Wu, Z., Li, Q. C., and Ye, W.: Design of a New Family of Kinematically Redundant Parallel Mechanisms With Two Rotations and One Translation, J. Mech. Design, 145, 053303, https://doi.org/10.1115/1.4056671, 2023.
Xu, L. M., Zhu, X., Ye, W., Li, Q. C., and Chen, Q. H.: Kinematic analysis and dimensional synthesis of a new 2R1T parallel kinematic machine, in: Proceedings of the Asme International Design Engineering Technical Conferences and Computers and Information in Engineering Conference (IDETC), Quebec, Canada, 26–29 August 2018, Paper No: DETC2018-85278, 9 pp., https://doi.org/10.1115/DETC2018-85278, 2018.
Xu, P., Li, B., Cheung, C.-F., and Zhang, J. F.: Stiffness modeling and optimization of a 3-dof parallel robot in a serial-parallel polishing machine, Int. J. Precis. Eng. Man., 18, 497–507, https://doi.org/10.1007/s12541-017-0060-1, 2017.
Yang, C., Chen, Q., Tong, J., and Li, Q. C.: Elastostatic Stiffness Analysis of a 2PUR-PSR Overconstrained Parallel Mechanism, Int. J. Precis. Eng. Man., 20, 569–581, https://doi.org/10.1007/s12541-019-00077-1, 2019.
Yang, C., Li, Q. C., and Chen, Q. H.: Natural frequency analysis of parallel manipulators using global independent generalized displacement coordinates, Mech. Mach. Theory, 156, 104145, https://doi.org/10.1016/j.mechmachtheory.2020.104145, 2021.
Yang, C., Ye, W., and Li, Q.: Review of the performance optimization of parallel manipulators, Mech. Mach. Theory, 170, 104725, https://doi.org/10.1016/j.mechmachtheory.2022.104725, 2022.
Zang, W., Zang, K., Shen, G., Li, X., and Li, G.: Position, Jacobian, decoupling and workspace analysis of a novel parallel manipulator with four pneumatic artificial muscles, J. Braz. Soc. Mech. Sci., 41, 148, https://doi.org/10.1007/s40430-019-1631-0, 2019.
Zhang, D. and Gao, Z.: Optimization design of a spatial six-degree-of-freedom parallel manipulator based on genetic algorithms and neural networks, in: Proceedings of the ASME 2008 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference (IDETC), Brooklyn, New York, USA, 3–6 August 2008, 767–775, https://doi.org/10.1115/DETC2008-49558, 2008.
Zhang, X. and Nelson, C. A.: Multiple-criteria kinematic optimization for the design of spherical serial mechanisms using genetic algorithms, J. Mech. Design, 133, 011005, https://doi.org/10.1115/1.4003138, 2011.
- Abstract
- Introduction
- Procedure of the multi-objective optimization design method
- Structure description of the 3RPS PM
- Objective functions of the 3RPS PM
- Multi-objective optimization analysis using the PCA and the neural network
- Conclusions
- Code and data availability
- Author contributions
- Competing interests
- Disclaimer
- Financial support
- Review statement
- References
- Abstract
- Introduction
- Procedure of the multi-objective optimization design method
- Structure description of the 3RPS PM
- Objective functions of the 3RPS PM
- Multi-objective optimization analysis using the PCA and the neural network
- Conclusions
- Code and data availability
- Author contributions
- Competing interests
- Disclaimer
- Financial support
- Review statement
- References