Comparative study of dynamically equivalent modeling methods for honeycomb sandwich structure: numerical simulations and experiments

The structure of the lightweight honeycomb sandwich panel is complex. Thus, establishing an equivalent simplified model is indispensable to improve the efficiency of the dynamic analysis of honeycomb sandwich panels. In this paper, three commonly used dynamically equivalent modeling methods for honeycomb sandwich panel are studied: a dynamically equivalent method based on laminated plate theory, a single-layer plate equivalent method based on the theory of Hoff (1948), and an improved equivalent method based on Allen (1969). Using theoretical study, numerical simulations, and experiments, the applicability of these equivalent methods and the effect of design parameters on the dynamic characteristics are studied, and the optimal dynamically equivalent method for honeycomb sandwich panels is obtained.

1 Introduction

Honeycomb sandwich (HS) structure has been widely used in aerospace applications because of its high specific strength and high specific stiffness. For example, in the aviation field, the use of the HS structure on the US “Osprey” transport exceeds 50 % of the total weight; on the “B-2” stealth bomber, the weight of the HS structure is over 60 %; and a lot of HS structures have been used in the commercial aircraft produced by Airbus and Boeing (Chen and Qiu, 2018). In the aerospace field, HS structures have been widely used as satellite panels, instrument support plates, and launch vehicle fairings, among others (Zhou et al.,2017; Li, 1999). The honeycomb sandwich structure is also widely used in the automobile industry, especially for vehicle body applications (Wang et al., 2018).

To ensure the high performance and high reliability of aircraft structures, their structural design has changed from the traditional static design to a static–dynamic coupling design. A finite element (FE) model used for accurate and efficient dynamic analysis is the prerequisite in structural dynamic design (Hussain and Naeem, 2017; Wang and Fu, 2019). HS structure is mainly composed of two facing skins, a honeycomb core layer, and two adhesive layers. The honeycomb core layer contains many honeycomb cells, making it difficult to establish an efficient and accurate FE model. Thus, an equivalent modeling method is needed to simplify the dynamic FE model of the HS structure. As early as the 1950s, Allen (1969) began to study the equivalent simplification method of HS panel; he assumed that the core layer could only sustain shear loads and that the facing skin panel could not sustain lateral loads, and he derived equivalent material calculation formulas. To overcome the shortcomings of the Allen (1969) model, Gibson et al. (1982) used the Euler–Bernoulli beam theory to establish the equivalent mechanical model of an equal-wall thickness hexagonal honeycomb and derived its in-plane equivalent elastic parameters. However, the equivalent method of Gibson et al. (1982) does not consider the shear deformation of the core layer. As the ratio between the honeycomb wall thickness and the honeycomb side length increases, the dynamic analysis error increases. Masters and Evans (1996) and Kim and Al-Hassani (2001) used the tensile, bending, and shear deformation of the Euler beam model to describe the displacement field of the honeycomb wall. Reissner (1948) assumed that the interlaminar stresses and displacements are continuous along the thickness direction. Based on this, the HS panel can be equivalent to a thin plate with homogeneous materials. Hoff (1948) considered the bending stiffness of the panel based on the method of Reissner (1948). Stemming from the theory of sandwich structure bending from Reissner (1948), Wang et al. (2020) established a mechanical model of bending stiffness degradation for a soft-honeycomb sandwich structure by introducing the equivalent debonding coefficient of the adhesive and elastic modulus temperature dependence of panels. Malek and Gibson (2015) studied the effective elastic properties of periodic hexagonal honeycombs and provided more accurate estimates of all nine elastic constants. Liu et al. (2007) derived effective elastic constants of a corrugation hybrid core using a micromechanics-based model and the homogenization method. Ongaro et al. (2016) investigated the in-plane elastic properties of hierarchical composite cellular materials by considering the hierarchy. They provided possible ways to improve the low-weight cellular structures by mixing different materials.

In addition to the above analytical methods, Mujika et al. (2011) used the finite element method (FEM) combined with static and dynamic tests to obtain the out-of-plane equivalent elastic modulus of the HS panel. Compared with the results obtained by the modified Gibson (1982) method, it is found that the tensile modulus obtained using FEM is in good agreement with the experimental results, but the shear modulus is higher than the test results. To study the dynamics of HS panels, Bardell et al. (1997) used the FEM to establish a dynamic model with free boundary conditions, and they performed modal analysis. Zhou and Li (1996) utilized a finite spline method to build a dynamic model of HS panel. At the same time, Yuan and Dawe (2002) used an improved finite spline method with cubic spline interpolation to establish a dynamic model of HS panel, which can improve the modeling accuracy. Zhang et al. (2018) derived the governing equations of HS panel based on Hamilton's theory and Reddy's third-order shear deformation theory. The modal characteristics were analyzed using the Rayleigh–Ritz method, and the nonlinear response was also studied. Wang et al. (2019) proposed a two-dimensional equivalent model for the hierarchical composite HS core layer following an orthotropic constitutive model, and they predicted the vibration of HS panels. Mukhopadhyay and Adhikari (2016) developed closed formulas for the out-of-plane shear moduli of spatially irregular honeycombs using minimum potential energy theorem and minimum complementary energy theorem and subsequently furnished representative results for natural frequencies corresponding to low vibration modes of a sandwich panel with a high length-to-width ratio. Based on the model updating method, Sun and Cheng (2017) established an accurate FE model of the HS plate. For predicting the low-velocity impact response of HS structures, Gunes and Arslan (2016) developed a numerical model using the FEM in terms of the measurement results of contact forces and absorbed energies.

Building accurate FE models of HS structures is necessary for analyzing and optimizing the vibration that occurs in the engineering practices. After nearly 70 years of development, the dynamically equivalent modeling method based on laminated plate theory, the single-layer plate equivalent method based on the theory of Hoff (1948), and the improved Allen (1969) method have gradually become the most commonly used equivalent simplified modeling methods for HS panels. In the present study, these three equivalent methods are investigated and compared to verify each method's accuracy and reliability using the theoretical analysis, numerical simulations, and experimental study.

2 The dynamically equivalent modeling method of honeycomb sandwich structure

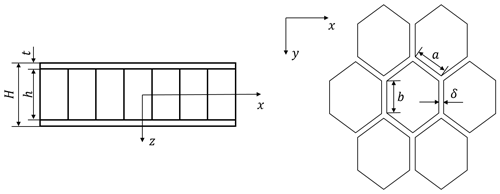
Figure 1 shows a typical single-wall thick HS structure, where H is the total thickness of the HS panel, h is the height of the core layer, t is the thickness of the facing skin, a is the length of the oblique wall of the honeycomb cell, b is the length of the straight wall of the honeycomb cell, and δ is the wall thickness of the honeycomb cell.

Figure 1 Honeycomb sandwich panel.

Figure 2 Fine finite element model of honeycomb sandwich panel.

2.1 The dynamically equivalent method based on laminated plate theory

The dynamically equivalent modeling method for HS structure based on laminated plate theory is to model the HS structure as a three-layer composite structure. The material properties of the facing skins and the core layer are considered separately, wherein the facing skins are assumed to be homogeneous layers, and all the material parameters are known. In addition, it is assumed that the core layer is a homogenous orthogonal anisotropic layer considering both in-plane and out-of-plane stiffness. Assuming that the core layer can resist lateral deformation and has a certain in-plane stiffness, the upper and lower facing skins work under Kirchhoff theory so that the honeycomb core layer can be equivalent to a homogenous equal thickness orthotropic layer. Further, assuming that there is normal stress in the x direction, the stress of the oblique cell wall can be analyzed using the equilibrium conditions. The elongation of the oblique wall and the equivalent strain in the x and y directions can then be calculated based on beam bending theory. Therefore, the equivalent Poisson's ratio and elastic modulus in the x direction can be derived using Hooke's law. Similarly, the equivalent Poisson's ratio and elastic modulus in the y direction can be derived. When deriving the equivalent properties in the z direction, the tensile stiffness of the honeycomb wall in the z direction can be calculated first, and we can then evenly equate it to the whole honeycomb cell; similarly, the elastic modulus in the z direction can also be obtained using the above method. Finally, the equivalent density of the honeycomb core layer is derived from the same mass before and after the equivalent. The specific derivation process is detailed in Gibson et al. (1982).

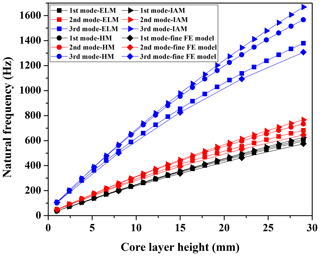
Figure 3 Effect of the core height on the natural frequencies of the honeycomb panel; the abbreviations ELM, HM, and IAM represent the dynamically equivalent modeling method based on the laminated plate theory, the single-layer plate equivalent method based on the Hoff (1948) theory, and the improved Allen (1969) equivalent method.

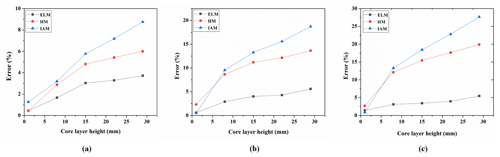
Figure 4 Comparison of the first three natural frequencies between three equivalent simplification methods and fine FE models.

For a non-normal hexagonal honeycomb cell, the equivalent formulas are as follows:

$$\begin{array}{}\text{(1)}& \left.\begin{array}{c}{\mathit{\rho }}_{c\mathrm{eq}}=\frac{\mathrm{2}}{\sqrt{\mathrm{3}}}\frac{\mathit{\delta }}{a}{\mathit{\rho }}_{\mathrm{s}}\\ E_{cx}=E_{\mathrm{s}}\frac{t^{\mathrm{3}}\cos \mathit{\theta }}{{\left(\frac{b}{a}+\sin \mathit{\theta }\right)}^{\mathrm{2}}{a}^{\mathrm{3}}}\frac{\mathrm{1}}{\mathrm{1}+{\cot }^{\mathrm{2}}\mathit{\theta }\frac{{\mathit{\delta }}^{\mathrm{2}}}{a^{\mathrm{2}}}}\\ E_{cy}=E_{\mathrm{s}}\frac{\left(\frac{b}{a}+\sin \mathit{\theta }\right)}{{\cos }^{\mathrm{3}}\mathit{\theta }}\frac{{\mathit{\delta }}^{\mathrm{3}}}{a^{\mathrm{3}}}\frac{\mathrm{1}}{\mathrm{1}+\left({\tan }^{\mathrm{2}}\mathit{\theta }+\frac{b}{a{\cos }^{\mathrm{2}}\mathit{\theta }}\right)\frac{{\mathit{\delta }}^{\mathrm{2}}}{a^{\mathrm{2}}}}\\ E_{cz}=\frac{\mathrm{3}\left(a+b\right)\mathit{\delta }}{\mathrm{4}\left(ab\cos \mathit{\theta }+a^{\mathrm{2}}\cos \mathit{\theta }\sin \mathit{\theta }\right)}{E}_{\mathrm{s}}\\ v_{cxy}=\frac{{\cos }^{\mathrm{2}}\mathit{\theta }}{\left(\frac{b}{a}+\sin \mathit{\theta }\right)\sin \mathit{\theta }}\frac{\mathrm{1}-\frac{{\mathit{\delta }}^{\mathrm{2}}}{a^{\mathrm{2}}}}{\mathrm{1}+{\cot }^{\mathrm{2}}\mathit{\theta }\frac{{\mathit{\delta }}^{\mathrm{2}}}{a^{\mathrm{2}}}}\\ v_{cyz}=v_{cxz}=\frac{\left(\frac{b}{a}+\sin \mathit{\theta }\right)\sin \mathit{\theta }}{{\cos }^{\mathrm{2}}\mathit{\theta }}\frac{{\mathit{\delta }}^{\mathrm{3}}}{a^{\mathrm{3}}}\frac{\mathrm{1}-\frac{{\mathit{\delta }}^{\mathrm{2}}}{a^{\mathrm{2}}}}{\mathrm{1}+\left({\tan }^{\mathrm{2}}\mathit{\theta }+\frac{b}{a{\cos }^{\mathrm{2}}\mathit{\theta }}\right)\frac{{\mathit{\delta }}^{\mathrm{2}}}{a^{\mathrm{2}}}}\\ G_{cxy}=E_{\mathrm{s}}{\left(\frac{\mathit{\delta }}{a}\right)}^{\mathrm{3}}\frac{\left(b/a+\sin \mathit{\theta }\right)}{{\left(b/a\right)}^{\mathrm{2}}\left[b/a+\mathrm{2}\left(\mathrm{1}-\sin \mathit{\theta }\right)\right]\cos \mathit{\theta }}\\ G_{cxz}=\frac{\mathit{\delta }\cos \mathit{\theta }}{b+a\sin \mathit{\theta }}{G}_{\mathrm{s}}\\ G_{cyz}=\frac{\mathit{\delta }\left(b+a\sin \mathit{\theta }\right)}{a\cos \mathit{\theta }\left(a+\mathrm{2}b\right)}{G}_{\mathrm{s}}\end{array}\right\},\end{array}$$

where ρ_s, E_s, and G_s are the density, elastic modulus, and shear modulus of the core layer, respectively; a is the length of the oblique wall of the honeycomb cell, b is the length of the straight wall of the honeycomb cell, and δ is the wall thickness of the honeycomb cell; θ is the angle between the oblique wall and the x axis; ρ_ceq is the equivalent density of the core layer; E_cx, E_cy, and E_cz are the equivalent elastic modulus in the x, y, and z directions, respectively; G_cxy, G_cyz, and G_cxz are the equivalent shear modulus in the xy, yz, and xz planes, respectively; and v_cxy and v_cyz are the equivalent Poisson's ratios.

Table 1 Equivalent material parameters of the honeycomb core layer of the dynamically equivalent modeling method based on the laminated plate theory (ELM).

Table 2 Equivalent material parameters of the single-layer plate equivalent method based on the Hoff (1948) theory (HM) and the improved Allen (1969) equivalent method (IAM).

2.2 The single-layer plate equivalent method based on Hoff (1948)

The basic idea of the single-layer equivalent model based on the theory of Hoff (1948) is to make an original HS structure equivalent to a homogenous and isotropic single-layer plate model. The transverse shear stiffness of the core layer and the bending stiffness of the facing skins are also considered. The basic assumptions used in the abovementioned theory are as follows (Hoff, 1948):

1. Assume that the upper and lower facing skins are ordinary thin plates.

2. As the core layer is soft, the in-plane stress component is ignored, i.e., ${\mathit{\sigma }}_{cx}={\mathit{\sigma }}_{cy}={\mathit{\tau }}_{cxy}=\mathrm{0}$.

3. Assume that σ_z is zero in the facing skins and core layer.

Based on the abovementioned basic assumptions, the HS plate can be simplified into a homogenous plate. According to the principle of stiffness equivalent, we make the bending stiffness and in-plane tensile and compressive stiffness derived from the Hoff (1948) equal to the corresponding values derived from the plate theory; thus, the equivalent parameters of the equivalent plate can be obtained. Similarly, the equivalent density can also be obtained. The specific expression is as follows:

$$\begin{array}{}\text{(2)}& \left.\begin{array}{l}\begin{array}{l}{\mathit{\nu }}_{\mathrm{eq}}={\mathit{\nu }}_{\mathrm{f}}\\ H_{\mathrm{eq}}=\sqrt{t^{\mathrm{2}}+\mathrm{3}{\left(h+t\right)}^{\mathrm{2}}}\\ E_{\mathrm{eq}}=\mathrm{2}{E}_{\mathrm{f}}t/H_{\mathrm{eq}}\\ G_{x\mathrm{eq}}=\frac{G_{cxz}{\left(h+t\right)}^{\mathrm{2}}}{h{H}_{\mathrm{eq}}}\\ G_{y\mathrm{eq}}=\frac{G_{cyz}{\left(h+t\right)}^{\mathrm{2}}}{h{H}_{\mathrm{eq}}}\end{array}\\ {\mathit{\rho }}_{\mathrm{eq}}=\frac{\mathrm{2}t{\mathit{\rho }}_{\mathrm{f}}+h{\mathit{\rho }}_{c\mathrm{eq}}}{H_{\mathrm{eq}}}\end{array}\right\},\end{array}$$

where ρ_ceq, G_cxz and G_cyz are derived from Eq. (1); h is the height of the core layer, and t is the thickness of the facing skin; ρ_f, ν_f, and E_f are the density, Poisson's ratio, and elastic modulus of the facing skins, respectively; and ρ_eq, ν_eq, E_eq, H_eq, G_xeq, and G_yeq are the equivalent density, equivalent Poisson's ratio, equivalent elastic modulus, equivalent height, and equivalent shear modulus of the equivalent single-layer plate, respectively.

Table 3 Comparison of the first six natural frequencies of the honeycomb panel.

Table 4 Equivalent material parameters of the honeycomb core layer of the dynamically equivalent modeling method based on the laminated plate theory (ELM).

2.3 The improved Allen (1969) equivalent method

In the Allen (1969) model, it is assumed that the core layer can only sustain transverse shear stress, ignoring its in-plane stiffness and bending stiffness. It is assumed that the upper and lower panels follow the Kirchhoff hypothesis and can only sustain the in-plane stress. However, when the height of the core layer is large relative to the facing skins' thickness, a significant analysis error occurs because the bending stiffness of the core layer is not considered.

The improved Allen (1969) model solves the abovementioned problem by introducing the bulk modulus K of the core layer. First, the material properties of the honeycomb core layer can be equivalent to a uniform isotropic material, so the in-plane stress–strain matrix of the core layer can be established. Furthermore, when the total bending moment and shearing force of the honeycomb sandwich structure are equal to those of the single-layer equivalent plate, the equivalent material parameters can be derived as follows:

$$\begin{array}{}\text{(3)}& \left.\begin{array}{l}{E}_{\mathrm{eq}}=\frac{\mathrm{12}\left(\mathrm{1}-{\mathit{\upsilon }}_{\mathrm{eq}}^{\mathrm{2}}\right)}{{\left(h+\mathrm{2}t\right)}^{\mathrm{3}}}\left(D+\frac{\mathrm{1}}{\mathrm{12}}K{h}^{\mathrm{3}}\right)\\ {\mathit{\upsilon }}_{\mathrm{eq}}=\frac{D{\mathit{\upsilon }}_{\mathrm{f}}+\frac{\mathrm{1}}{\mathrm{12}}K{h}^{\mathrm{3}}}{D+\frac{\mathrm{1}}{\mathrm{12}}K{h}^{\mathrm{3}}}\\ G_{x\mathrm{eq}}=G_{cxz}\frac{h+t}{h+\mathrm{2}t}\\ G_{y\mathrm{eq}}=G_{cyz}\frac{h+t}{h+\mathrm{2}t}\end{array}\right\},\end{array}$$

where G_cxz and G_cyz are derived from Eq. (1); h is the height of the core layer, and t is the thickness of the facing skin; K is the bulk modulus of the core layer; and D denotes the bending stiffness of the HS panel.

$$\begin{array}{}\text{(4)}& {\displaystyle }K={\displaystyle \frac{\mathit{\delta }}{\mathrm{2}\sqrt{\mathrm{3}}a}}{E}_{\mathrm{s}}\text{(5)}& {\displaystyle }D={\displaystyle \frac{E_{\mathrm{f}}{\left(h+t\right)}^{\mathrm{2}}t}{\mathrm{2}\left(\mathrm{1}-{\mathit{\nu }}_{\mathrm{f}}^{\mathrm{2}}\right)}},\end{array}$$

where E_s is the elastic modulus of the core layer; a is the length of the oblique wall of the honeycomb cell, and δ is the wall thickness of the honeycomb cell; ν_f and E_f are the Poisson's ratio and elastic modulus of the facing skins, respectively; h is the height of the core layer, and t is the thickness of the facing skin.

In summary, the dynamically equivalent method based on laminated plate theory contains all of the original material parameters, and the honeycomb core material is assumed to be orthogonal anisotropic material, which will be closer to the actual situation. However, the computational cost of modeling and analysis is also higher. The single-layer plate equivalent method based on the theory of Hoff (1948) has fewer equivalent material parameters. The disadvantage is that the equivalent thickness of the equivalent plate is different from that of the original honeycomb panel. It is challenging to construct a reasonable model for complex structures. The improved Allen (1969) equivalent method also uses a few equivalent material parameters to model the honeycomb sandwich structure, and the equivalent thickness is the same as the original structure. Hereinafter, the abbreviations ELM, HM, and IAM represent the dynamically equivalent modeling method based on the laminated plate theory, the single-layer plate equivalent method based on the theory of Hoff (1948), and the improved Allen (1969) equivalent method, respectively.

Table 5 Equivalent material parameters of the single-layer plate equivalent method based on the Hoff (1948) theory (HM) and the improved Allen (1969) equivalent method (IAM).

Figure 5 Effect of the facing skin thickness on the dynamic characteristics.

3 Application analysis of the equivalent modeling method for honeycomb sandwich panel

Generally, plates are divided into thin plates (thickness ∕ side length <0.01), medium-thickness plates (0.1< thickness/side length <0.01), and thick plates (thickness/side length >0.1). To verify the applicability of the three equivalent simplified modeling methods introduced in Sect. 2 for the dynamic modeling of HS panels, a free-boundary aluminum HS panel model is utilized, which is 600 mm × 287 mm. The thickness of the upper and lower facing skin is 0.5 mm. The core layer is composed of regular hexagonal single-walled aluminum honeycomb cells, and the ratio of the wall thickness δ to the side length a, i.e., $\frac{\mathit{\delta }}{a}$, is 0.0128. The elastic modulus, Poisson's ratio, and density of the aluminum material are 70 GPa, 0.33, and 2700 kg m⁻³, respectively. The fine FE model is shown in Fig. 2. The face skins and the honeycomb wall are meshed by the S4R element in Abaqus, and the connection between the facing skin and core layer is established with a tie constraint.

Figure 6 Effect of the elastic modulus of the facing skin on the dynamic characteristics.

Figure 7 Effect of the elastic modulus of core layer on the dynamic characteristics.

Figure 8 Effect of $\frac{\mathit{\delta }}{a}$ on the dynamic characteristics (0.001–0.015).

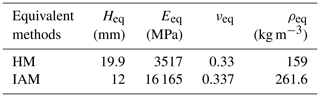
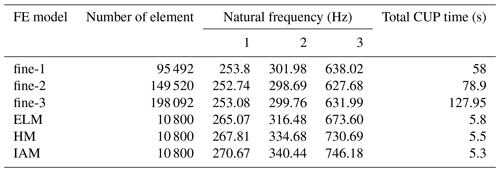
The simplified equivalent FE models are all meshed using the S4R elements in Abaqus. However, the sectional proprieties selected for each FE modeling method are different: the sectional propriety used in ELM is composite shell section, whereas the HM and IAM use homogenous shell section. The Lanczos eigenvalue solution method is selected as the modal analysis method in this study. Before performing application analysis, we first verify the accuracy and the computational efficiency of these equivalent FE models. The core layer's height is selected as 11 mm. Three fine FE models with different mesh accuracy are established: 95 491, 149 520, and 198 092. The equivalent material parameters of the HS panel calculated using the three equivalent methods described in Sect. 2 are listed in Tables 1 and 2.

Figure 9 Aluminum honeycomb sandwich panel.

Table 6 Comparison of the first six natural frequencies of the honeycomb panel.

It can be seen from Table 3 that the maximum absolute error among the three fine FE models is only 10.34 Hz (i.e., the absolute error between the third modal frequency of fine-1 and fine-2). It shows that the fine FE model 3 (fine-3) has good mesh convergence, and we choose fine-3 as the reference model in the subsequent study. From the comparison of CPU calculation time, it can be seen that the computational efficiency of these simplified equivalent FE models is significantly higher than that of the fine FE model.

Keeping the other parameters constant, the height of the core layer is selected from 1 to 29 mm, and the total height of the HS panel ranges from 2 to 30 mm, including thin, medium, and thick plates. The core layer heights of the fine FE model are taken as 1, 8, 15, 22, and 29 mm. Figure 3 shows the effect of core height on the dynamic characteristics of the HS panel. Figure 4 shows the natural frequencies' error between the three equivalent simplification models and the fine FE model.

Figure 10 Field layout of the honeycomb plate modal test.

As the core layer height increases, the natural frequencies of the three equivalent simplification models and the fine FE model increase (Fig. 3). Due to the fact that the thickness of the core layer increases, the equivalent bending stiffness of the HS panel also increases. Furthermore, it shows that the natural frequencies obtained by the three equivalent simplification methods are larger than the corresponding value obtained by the fine FE model. It can be seen from Fig. 4 that when the HS panel is a thin plate, the error between the first three natural frequencies analyzed by three equivalent simplified methods and the results obtained by using the fine FE model is less than 5 %. However, with an increase in the thickness of the HS panel, the analysis accuracy is gradually reduced when using three equivalent simplified methods. When a height of 30 mm is reached, i.e., the HS panel has become a thick plate, the dynamic models established by the HM and IAM are no longer suitable for dynamic analysis, and the maximum respective errors of 19.92 % and 27.67 % are reached. Nevertheless, within the variable analysis range, the dynamic model established by the ELM has high analytical precision with a maximum error of only 5.60 %.

Therefore, the three equivalent modeling methods have higher accuracy in the analysis for thin HS plates, whereas the ELM has higher accuracy than the other two equivalent modeling methods for medium and thick HS plates.

4 Effect of parameters on the dynamic characteristics of honeycomb sandwich panels

According to Eqs. (1), (2), and (3), in addition to the core layer height, the main design parameters of a HS panel include the elastic modulus E_f and the thickness t of the facing skins, the elastic modulus E_s of the core layer, and the ratio between the wall thickness and the side length of the cell $\frac{\mathit{\delta }}{a}$. This section studies the effect of the design parameters on the dynamic characteristics of the HS plate using different equivalent dynamic modeling methods. The numerical simulation model used is the same as that used in Sect. 3.

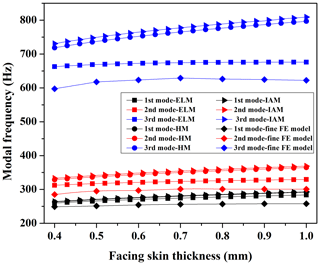
4.1 Effect of the facing skin thickness on dynamic characteristics

The facing skin thickness is selected from 0.4 to 1 mm, while the other design parameters remain constant. The first three modal frequencies are selected as the analysis object.

Table 7 Comparison of the first five modal frequency test results of three test panels.

Table 8 Equivalent material parameters of the honeycomb core layer of ELM.

Table 9 Equivalent material parameters of the Hoff (1948) theory (HM) and the improved Allen (1969) equivalent method (IAM).

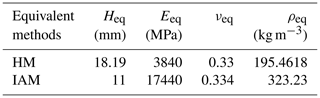
Table 10 Comparison of the modal assurance criterion (MAC) between test results and simulation results.

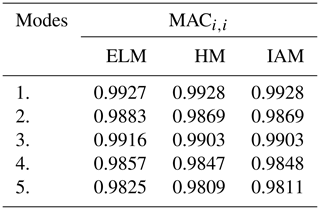
Table 11 Comparison of the first five natural frequencies between test results and simulation results.

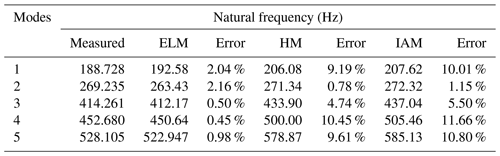
Figure 5 shows the effect of the facing skin thickness on the dynamic characteristics of the HS plate. The modal frequencies of HM and IAM increase linearly with the increase in facing skin thickness; however the change in the facing skin thickness has less effect on the analysis results when using ELM and the fine FE model. Moreover, the modal analysis results of the IAM are the largest, followed by the HM, and the ELM has the smallest modal analysis results, which are closest to the results from the fine FE model.

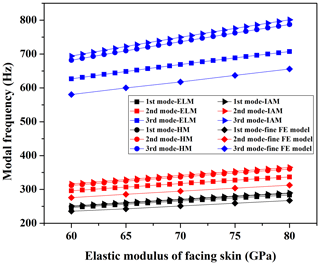
4.2 Effect of the elastic modulus of the facing skins on the dynamic characteristics

The values of the elastic modulus of the facing skins are selected from 60 to 80 GPa. The effect of the elastic modulus of the facing skins on the dynamic characteristics of HS structure is shown in Fig. 6 following the analysis.

With an increase in the elastic modulus of the facing skin, the modal frequencies obtained by the three equivalent modeling methods and the fine FE model increase linearly. With an increase in the mode order, the differences in the analytical results of the different equivalent methods also gradually increase. It is concluded from Fig. 6 that the effect of the facing skin's elastic modulus on the dynamic characteristic of the HS structure is obvious.

Figure 11 Test results of the first five modes of the honeycomb sandwich panel.

Figure 12 Simulation results of the first five modes of the honeycomb sandwich panel.

Figure 13 Modal assurance criterion (MAC).

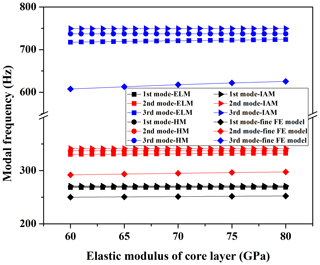
4.3 Effect of the elastic modulus of the core layer on the dynamic characteristics

The values of the elastic modulus of the core layer are also selected from 60 to 80 GPa. The effect of the elastic modulus of the core layer on the dynamic characteristics of HS structure is shown in Fig. 7 following the analysis.

The results indicate that the core layer's elastic modulus has little effect on the dynamic characteristics of the HS plate. The modal frequencies analyzed by HM do not vary with a change in the elastic modulus of the core layer, as this method ignores the contribution of the core layer to the equivalent bending stiffness of the HS structure, whereas the analysis results of the other three methods show a small increase.

4.4 Effect of $\frac{\mathit{\delta }}{a}$ on the dynamic characteristics

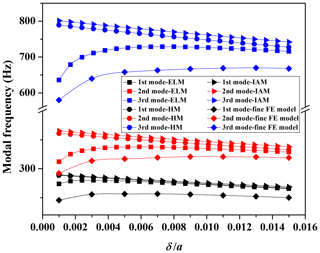
The ratios between the thickness and the side length of the cell wall, i.e., $\frac{\mathit{\delta }}{a}$, are selected from 0.001 to 0.015 mm. Figure 8 shows the effect of $\frac{\mathit{\delta }}{a}$ on the dynamic characteristics of the HS structure following the analysis.

It can be seen from Fig. 8 that the dynamic characteristics analyzed by HM and IAM decrease linearly with an increase in the $\frac{\mathit{\delta }}{a}$. However, the change in the results when using ELM and the fine FE model increases sharply to an extreme point, before it slowly decreases and tends to stabilize. The increase in $\frac{\mathit{\delta }}{a}$ can increase the equivalent stiffness of the core layer; this also leads to an increase in the mass of the HS plate. These two phenomena have an opposite effect on the dynamic characteristics of the HS structure. When the $\frac{\mathit{\delta }}{a}$ is smaller than the extreme point, the increase in the equivalent stiffness has a more significant effect on the dynamic characteristics than the mass increase on the dynamic characteristics, so the modal frequencies increase. When the $\frac{\mathit{\delta }}{a}$ becomes greater than the extreme point, the effect of the mass increase on the dynamic characteristics becomes larger, so the modal frequencies begin to decrease gradually; when we continue to increase $\frac{\mathit{\delta }}{a}$, the effect of $\frac{\mathit{\delta }}{a}$ on the modal frequency tends to balance.

As a result of the above analysis, it can be seen that the effect of the elastic modulus of facing skins and the core layer height on the dynamic characteristics of the HS plate are apparent, and their influence must be taken into account in the dynamic simulation modeling and dynamic analysis. In contrast, the effect of other design variables is relatively small.

5 Experimental study

For further validation of the equivalent modeling methods for HS structure, a thin HS panel and a medium HS panel are manufactured as experimental structures in the experimental validation.

5.1 Experimental validation on a thin honeycomb sandwich panel

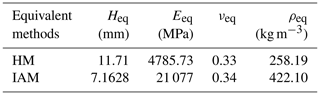
For the study of a thin HS panel, the experimental results of Raville and Ueng (1967) are used. The HS panel used in the experiment has a total thickness of 7.1628 mm; the thickness of the facing skins is 0.4064 mm; the lengths of the sides are 1828.8 and 1219.2 mm, respectively. The ratio between the thickness and the short side length of the panel is less than 0.01, and the panel is a typical thin plate. The experimental boundary condition is simply supported on four sides. The elastic modulus of the material is 68.948 GPa, the Poisson's ratio is 0.33, and the density is 2768 kg m⁻³. The equivalent material parameters of the HS panel calculated using the three equivalent methods described in Sect. 2 are listed in Tables 4 and 5.

The comparison of dynamic analysis results of three equivalent simplified models with the Raville and Ueng's (1967) test results is shown in Table 6.

It can be seen from Table 3 that the analytical results obtained using the three equivalent simplification methods are in good agreement with the corresponding experimental results. The maximum error is less than 4 %. The results also validate that when the HS panel is a thin plate, the three equivalent methods have good applicability to the dynamic modeling of HS structures. Among them, the ELM has the highest accuracy, followed by HM, and the IAM has the highest error.

5.2 Experimental validation on a medium honeycomb sandwich panel

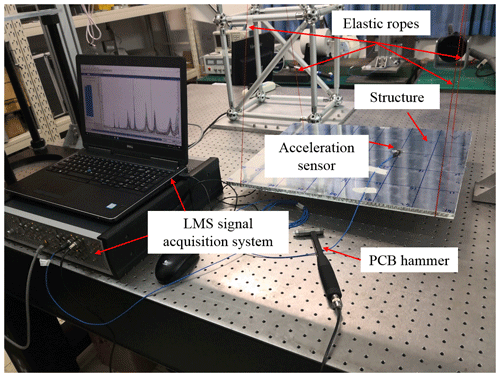
To validate the accuracy of the three equivalent modeling methods in the analysis of a medium-thickness HS plate, we manufactured three identical aluminum HS panels commonly used in the engineering practice, as shown in Figure 9. The specific size of the test structure is 550 mm × 450 mm × 12 mm; the thickness of the facing skins is 0.5 mm. The ratio between the thickness and the short side length is 0.027>0.01, so the structures belong to a medium plate. The elastic modulus of the material is 70 GPa, the Poisson's ratio is 0.33, and the density is 2700 kg m⁻³.

The experimental setup is shown in Fig. 10, including the LMS signal acquisition system, a PCB 086C03 impact hammer (sensitivity of 2.267 mV N⁻¹), and a PCB 333B30 acceleration sensor (sensitivity of 100.5 mV g⁻¹). The structure is suspended with elastic ropes to simulate free-free boundary conditions. The modal test is performed using the “moving excitation point method”. To eliminate the effect of test noise, each test point is tested three times and averaged.

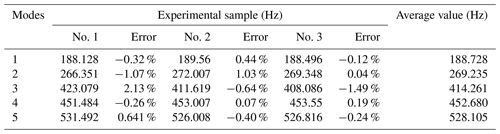
The first five order mode shapes identified from the modal test datum are shown in Fig. 11. The measured nature frequencies are listed in Table 7. In Table 7, the relative error indicates the error between the test results of each plate and the average values.

The results show that the manufacturing error of the HS structure utilized in the experiment has a relatively small effect on the dynamic characteristics, and the maximum relative error is only 2.13 %.

The equivalent material parameters of the HS panel calculated using the three equivalent methods described in Sect. 2 are listed in Tables 8 and 9. Three equivalent FE models are then established using Abaqus software, and modal analysis is carried out. The first five modes are obtained, as shown in Fig. 12 (because the three equivalent models have similar modal shapes, only the modal shapes analyzed by ELM are shown).

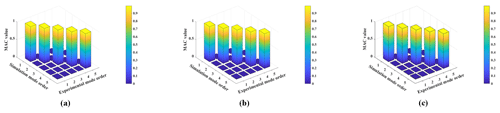
The modal assurance criterion (MAC) values between the mode shapes obtained using different equivalent models and the test mode shape are shown in Fig. 13, and the diagonal values are listed in Table 10.

$$\begin{array}{}\text{(6)}& {\mathrm{MAC}}_{i,j}={\displaystyle \frac{{\left({\mathit{\varphi }}_{E,i}^T{\mathit{\varphi }}_{A,j}\right)}^{\mathrm{2}}}{\left({\mathit{\varphi }}_{E,i}^T{\mathit{\varphi }}_{E,i}\right)\left({\mathit{\varphi }}_{A,j}^T{\mathit{\varphi }}_{A,j}\right)}},\end{array}$$

where ϕ_E,i denotes the ith experimental mode shape, and ϕ_A,j denotes the jth analytical mode shape.

The diagonal values of the three MACs are all greater than 0.98, and the non-diagonal values are less than 0.01, indicating that the modes obtained using the three equivalent models agree well with the experimental results. The comparison of the first five natural frequencies between test results and simulation results is shown in Table 11.

It can be seen from Table 11 that the dynamic characteristics obtained by the ELM are in a good agreement with the experimental results, and the maximum relative error is only 2.16 %. The analysis results obtained using the other two equivalent modeling methods are larger than the test results, and the maximum error exceeds 10 %. The comparison of the results from Table 3 further validates the applicability analysis results in Sect. 3. When the HS panel is a medium-thickness plate, the ELM still has high accuracy, but the dynamic models established by HM and IAM have larger errors than the actual value.

6 Conclusions

In this paper, three equivalent modeling methods are used to simulate the dynamic model of honeycomb structures. The applicability of the three equivalent modeling methods for HS panels with different thicknesses and the effect of design parameters on the dynamic characteristics are studied using numerical simulations and experiments. The main conclusions are as follows:

1. For a thin HS panel, all three equivalent modeling methods have high accuracy. When compared with the analysis results of fine FE model and the test results, the errors are less than 5 % and 4 %, respectively. When the HS panel becomes a medium-thickness plate or a thick plate, the ELM still has high accuracy, but the HM and IAM have analysis errors that are too high and are no longer suitable for the dynamic modeling of HS structure. Among the methods discussed, the IAM has the worst analysis accuracy.

2. The effect of the thickness and modulus of the facing skins and the height and modulus of the core layer on the dynamic characteristics of the HS plate is that the modal frequencies increase as the design variable increases; however, when the ratio between the wall thickness and the size length of the cell increases, the modal frequencies first increase and then slowly decrease before finally stabilizing. Among these design parameters, the effect of the elastic modulus of facing skins and the core layer height on the dynamic characteristics of HS plate are apparent, whereas the effect of other design variables is relatively small.

3. From the theoretical modeling process, it can be seen that the ELM considers more modeling details than the HM or IAM; in particular, it considers the tensile and shear stiffness of the core layer in different directions; therefore, it is more suitable for analyzing the HS medium and thick panels.