Design and implementation of speed fluctuation reduction for a ball screw feed system at low-speed operation

In the high-precision servo feed system, when the permanent magnet synchronous motor (PMSM) is operated at low speed in the classical drive feed system (CDFS), the speed fluctuation caused by the motor torque harmonics seriously affects the speed smoothness of the servo system. In this paper, a novel double-drive differential feed system (DDFS) is proposed to effectively suppress the effect of torque harmonics of PMSM on speed fluctuation of the linear feed system at low-speed operation. Firstly, the effect of motor torque harmonics on motor speed for the DDFS is analyzed by the sensitivity function of the servo system, which indicates that the torque harmonics have little effect on the motor speed at high-speed operation. Then, in the DDFS, we make two motors rotate in the same direction at high speed and differentially synthesize at the ball screw to obtain low-velocity linear motion. Compared with the CDFS, the DDFS can suppress the effect of motor torque harmonics on speed fluctuation of the table and improve speed smoothness at low-speed operation.

1 Introduction

In the high-precision manufacturing industry, higher requirements are placed on the dynamic response speed and speed smoothness of the servo feed system at low speed. Permanent magnet synchronous motors (PMSMs) are widely used in high-precision servo feed systems since they have high reliability, efficiency, and a torque inertia ratio with a fast dynamic response (Pillay, 1990; Jahns and Soong, 1996). However, when the motor is rotating at low speed, the speed fluctuation caused by motor torque harmonics will seriously affect the performance of the servo system (Houari et al., 2018; Qian et al., 2004). According to the difference of frequency values, the torque harmonics of the PMSM can be divided into the low-frequency components and the high-frequency components. The high-frequency components can be effectively suppressed by controlling loop bandwidths, and the low-frequency components within the controlling loop bandwidths need special handling (Houari et al., 2018; Chan et al., 1994). Therefore, in order to increase the speed smoothness of the servo system, when the motor operates at low speed, it is necessary to suppress the low-frequency components that cause the motor torque fluctuation.

The speed fluctuation of a PMSM is affected by many factors at low speed, e.g., cogging torque, current measurement errors, and flux harmonics (Guemes et al., 2011; Gebregergis et al., 2015). To effectively reduce the speed fluctuation, many valuable methods have been proposed and verified to suppress motor torque ripple. Generally, these methods are usually divided into two groups. The first group focuses on motor design improvement, such as skewing the slot or magnet (Binns et al., 1993; Carlson et al., 1989), using a fractional number of slots per pole (Chung et al., 2012; Senol and Ustun, 2011; Donato et al., 2010; Cavagnino et al., 2013), or optimizing the winding distribution (Nakao et al., 2014; Gebregergis et al., 2015). The torque ripple can be effectively reduced by optimizing the motor design. However, the optimization of motor design is limited by the development of new technologies, and they can result in higher manufacturing cost and a further complicated realization. The second group uses advanced control methods, which regulate the input current or voltage to reduce torque ripple (Panda et al., 2008). Houari et al. (2018, 2015) proposed an effective method to reduce speed fluctuation of PMSM at low speed, which improved the conventional PMSM controller by superposing an appropriate compensation signal on the quadratic-current reference. Xia et al. (2015) proposed a speed and current proportional–integral–resonant (PIR) control strategy to reduce speed fluctuation for the low-speed high-torque PMSM drive system. Qian et al. (2005) proposed two iterative learning control (ILC) schemes implemented in the time domain and frequency domain, respectively, to suppress speed ripples due to torque ripple at low speed. Using a robust iterative learning control algorithm (ILC) based on an adaptive sliding mode control (SMC) technique, the motor torque ripple was effectively suppressed, and the anti-interference ability of the servo system was improved (Liu et al., 2018). Tan et al. (2011) proposed the identification and compensation method of torque ripple based on steady-state error analysis, in which the function of torque ripple was determined by the least-squares method and the compensation of torque ripple was achieved by a programmable multi-axis controller (PMAC). The advantage of the above method is that the controller is a component of the servo system and does not require additional hardware. However, this method requires a special control algorithm to be written, which is complicated to implement.

In this paper, a novel DDFS is proposed to reduce the influence of torque harmonics of PMSM on velocity fluctuations of a table for a linear feed system at low-velocity operation. In the DDFS, the screw and nut are both driven by PMSMs, which rotate in the same direction at high speed and differentially synthesize at the ball screw pair to obtain low-velocity linear motion. This design ensures the driven table travels at low velocity while guaranteeing the two motors rotate at high speed, in which the high-frequency components of the torque ripples limited by the bandwidth of the servo system suppress the influence of the motor torque ripple on the velocity fluctuation of the table. Compared with the CDFS, the DDFS can reduce the effect of motor torque harmonics on the speed fluctuation of the table and improve speed smoothness at low-speed operation.

The remainder of this paper is arranged as follows. The DDFS structure and its control strategy are described in Sect. 2. The speed fluctuation caused by motor torque harmonics is analyzed in Sect. 3. The influence of motor torque harmonics on motor speed for the DDFS is analyzed by the sensitivity function of the servo system in Sect. 4. The velocity fluctuations of the table for the DDFS compared with the CDFS are simulated in Sect. 5. The experimental results validate the effectiveness of the proposed method in Sect. 6. The paper is concluded in Sect. 7.

2 The DDFS description

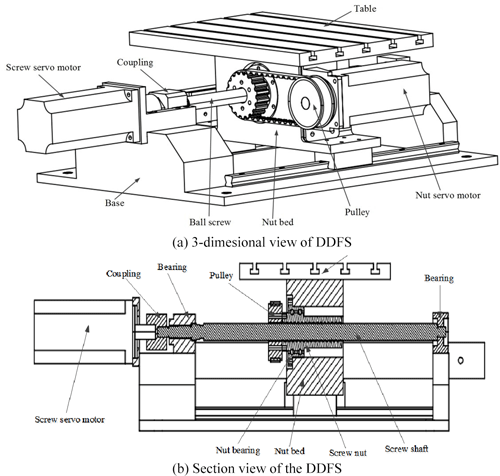
2.1 The DDFS structure

In the CDFS, the screw shaft is driven by a servo motor through a coupling and the rotary motion of a motor is converted into linear motion of the table. Compared with the CDFS, the DDFS structure based on the nut-driven ball screw pair is illustrated in Fig. 1.

Figure 1 The DDFS structure.

In the DDFS, the screw shaft and screw nut are both driven by PMSMs, which rotate in the same direction at high speed and differentially synthesize though the ball screw pair to obtain low velocity of the table. This design ensures the driven table travels at low velocity while guaranteeing the two motors rotate at high speed. Superposing two rotating speeds of PMSMs at high speed by the ball screw pair, the driven table could obtain low velocity and effectively avoid the crawling zone of the motors at low speed (Du et al., 2018a, b, 2017; Yu and Feng, 2015). In the DDFS, when the nut servo motor does not rotate, the DDFS changes to the CDFS.

2.2 PMSM model

Assuming that the PMSM iron loss, eddy current loss, and hysteresis loss are not considered, the d–q axis current equation in the stator d–q axis rotation reference coordinate system can be described as follows:

$$\begin{array}{}\text{(1)}& {\displaystyle \frac{\mathrm{d}}{\mathrm{d}t}}{i}_d={\displaystyle \frac{-R_{\mathrm{s}}}{L_d}}{i}_d+{\displaystyle \frac{{\mathit{\omega }}_{\mathrm{e}}{L}_q}{L_d}}{i}_q+{\displaystyle \frac{\mathrm{1}}{L_d}}{u}_d,\text{(2)}& {\displaystyle \frac{\mathrm{d}}{\mathrm{d}t}}{i}_q={\displaystyle \frac{-R_{\mathrm{s}}}{L_q}}{i}_q-{\displaystyle \frac{{\mathit{\omega }}_{\mathrm{e}}{L}_d}{L_q}}{i}_d-{\displaystyle \frac{{\mathit{\omega }}_{\mathrm{e}}{\mathit{\psi }}_{\mathrm{f}}}{L_q}}+{\displaystyle \frac{\mathrm{1}}{L_q}}{u}_q,\text{(3)}& {\displaystyle \frac{\mathrm{d}}{\mathrm{d}t}}{\mathit{\omega }}_{\mathrm{e}}={\displaystyle \frac{p}{J_{\mathrm{M}}}}\left(T_{\mathrm{e}}-T_{\mathrm{L}}-{\displaystyle \frac{B}{p}}{\mathit{\omega }}_{\mathrm{e}}\right),\text{(4)}& {\displaystyle \frac{\mathrm{d}}{\mathrm{d}t}}{\mathit{\theta }}_{\mathrm{e}}={\mathit{\omega }}_{\mathrm{e}},\end{array}$$

where p is the number of pole pairs, ω_e is the electrical angular speed, R_s is the stator resistance, u_d and u_q are the voltages of the stator along the d and q axes, respectively, L_d and L_q are the inductances of the stator along the d and the q axes, respectively, i_d and i_q are the currents of the stator along the d and q axes, respectively, T_L is the load torque, T_e is the electromagnetic torque, B is the viscous friction coefficient equivalent to the motor shaft, and J_M is the moment of inertia equivalent to the motor shaft, including the motor shaft moment of inertia, the screw moment of inertia, the coupling moment of inertia, and the mass of the table.

When the i_d=0 vector control is performed on the PMSM, the electromagnetic torque of the motor is largest, and the electromagnetic torque can be shown as follows:

$$\begin{array}{}\text{(5)}& T_{\mathrm{e}}=p\left[{\mathit{\psi }}_{\mathrm{f}}{i}_q+\left(L_d-L_q\right)i_d{i}_q\right].\end{array}$$

For the surface-mounted PMSM used in this paper, L_d and L_q are equal and the electromagnetic torque is simplified as follows:

$$\begin{array}{}\text{(6)}& T_{\mathrm{e}}=p{\mathit{\psi }}_{\mathrm{f}}{i}_q.\end{array}$$

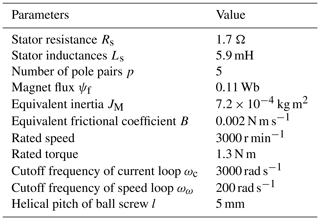
The parameters of the servo system for the DDFS are shown in Table 1.

Table 1 Parameters of the servo system for the DDFS.

2.3 Control strategy of the DDFS

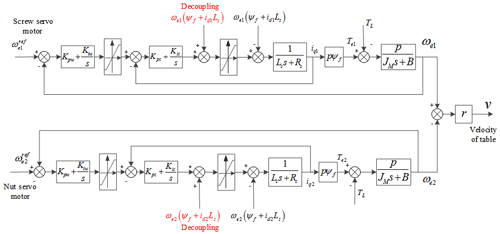
The speed fluctuation of the DDFS is mainly studied in this paper; therefore, the PMSMs are set to work under the speed loop. The conventional PI control strategy is adopted for the PMSMs with the same parameters selected. The control strategy of the DDFS is shown in Fig. 2.

Figure 2 Control strategy of the DDFS.

When the velocity of the table $v=v_{{\mathrm{ref}}_{\mathrm{e}\mathrm{1}}}-v_{{\mathrm{ref}}_{\mathrm{e}\mathrm{2}}}$ is required, the velocity signals $v_{{\mathrm{ref}}_{\mathrm{e}\mathrm{1}}}=\mathit{\omega }{\mathrm{ref}}_{\mathrm{e}\mathrm{1}}\cdot r$ of the screw motor and $v_{{\mathrm{ref}}_{\mathrm{e}\mathrm{2}}}=\mathit{\omega }{\mathrm{ref}}_{\mathrm{e}\mathrm{2}}\cdot r$ of the nut servo motor are given by the servo drivers of the two motors, respectively. The velocity of the table can be obtained by the ball screw pair.

$$\begin{array}{}\text{(7)}& {\displaystyle }v=\left({\mathit{\omega }}_{\mathrm{e}\mathrm{1}}-{\mathit{\omega }}_{\mathrm{e}\mathrm{2}}\right)r\text{(8)}& {\displaystyle }r={\displaystyle \frac{l}{\mathrm{2}\mathit{\pi }p}},\end{array}$$

where v is the velocity of the table, ω ref_e1 and ω ref_e2 are the electrical angular speed reference value of the screw servo motor and the electrical angular speed reference value of the nut servo motor, respectively, r is the transmission coefficient, l is the helical pitch of the ball screw, and p is the number of poles of the PMSM.

The current loop controller and speed loop controller are designed by a simple pole placement strategy. When the current loop bandwidth is selected, the current loop adjustment response time is required to be as small as possible and the current loop is required to have good disturbance performance. When selecting the speed loop bandwidth, it is necessary to ensure a better control target while avoiding mutual interference between the current loop and the speed loop.

The control parameters of the current loop and speed loop are as follows:

$$\begin{array}{}\text{(9)}& {\displaystyle }{K}_{\mathrm{pc}}=\mathrm{2}\mathit{\xi }{L}_{\mathrm{s}}{\mathit{\omega }}_{\mathrm{c}}-R_{\mathrm{s}},\text{(10)}& {\displaystyle }{K}_{\mathrm{ic}}=L_{\mathrm{s}}{\mathit{\omega }}_{\mathrm{c}}^{\mathrm{2}},\text{(11)}& {\displaystyle }{K}_{p\mathit{\omega }}={\displaystyle \frac{\mathrm{2}\mathit{\xi }{J}_{\mathrm{M}}{\mathit{\omega }}_{\mathit{\omega }}}{p^{\mathrm{2}}{\mathit{\psi }}_{\mathrm{f}}}},\text{(12)}& {\displaystyle }{K}_{i\mathit{\omega }}={\displaystyle \frac{J_{\mathrm{M}}{\mathit{\omega }}_{\mathit{\omega }}^{\mathrm{2}}}{p^{\mathrm{2}}{\mathit{\psi }}_{\mathrm{f}}}},\end{array}$$

where K_pc is the current loop proportional gain, K_ic is the current loop integral gain, ξ is the damping coefficient, ξ=0.7, ω_c is the current loop cutoff frequency, K_pω is the speed loop proportional gain, K_iω is the speed loop integral gain, and ω_ω is the speed loop cutoff frequency.

3 Speed fluctuation analysis of a PMSM at low speed

When the PMSM is controlled at low speed, the main influence factors for the speed fluctuation of a motor are current sensor offset error, gain mismatch, and flux harmonics.

3.1 Current sensor offset error

Due to the dc offsets present during phase current detection and controller input conversion, the phase current measured by the sensor is deviated. The torque ripple due to the stator current measurement error can be expressed as follows (Houari et al., 2018):

$$\begin{array}{}\text{(13)}& T_{\mathrm{em}\mathrm{1}}=\mathit{\beta }\cos \left({\mathit{\theta }}_{\mathrm{e}}+\mathit{\alpha }\right)\sqrt{\mathrm{\Delta }{i}_a^{\mathrm{2}}+\mathrm{\Delta }{i}_a\mathrm{\Delta }{i}_b+\mathrm{\Delta }{i}_b^{\mathrm{2}}},\end{array}$$

where Δi_a and Δi_b are the offset errors, β is a constant, θ_e is the electrical angle, and α is a constant displacement of the angle.

3.2 Gain mismatch

The frequency of the torque ripple caused by the current sampling error is twice the fundamental frequency, and the torque fluctuation caused by the current sampling error can be expressed as follows (Houari et al., 2018):

$$\begin{array}{}\text{(14)}& T_{\mathrm{em}\mathrm{2}}=\mathit{\gamma }\cos \left(\mathrm{2}{\mathit{\theta }}_{\mathrm{e}}-{\displaystyle \frac{\mathrm{2}\mathit{\pi }}{\mathrm{3}}}\right),\end{array}$$

where γ is the sensor gain deviation.

3.3 Flux harmonics

The non-sinusoidal flux linkage in the air gap is another factor that causes torque ripple. The torque harmonics of the 6th and multiples of the 6th caused by the non-sinusoidal flux linkage can be expressed as (Houari et al., 2018)

$$\begin{array}{}\text{(15)}& T_{\mathrm{FH}}=\sum _{i=\mathrm{1}}^n{T}_{\mathrm{6}i}\cos \left(\mathrm{6}i{\mathit{\theta }}_{\mathrm{e}}\right),\end{array}$$

where T_6i is the amplitude of the multiple of six harmonics.

3.4 Speed fluctuation analysis

The motor electromagnetic torque T_e can be expressed as the sum of the main dc component (T₀) and the harmonic components (ΔT).

$$\begin{array}{}\text{(16)}& {\displaystyle }{T}_{\mathrm{e}}=T_{\mathrm{0}}+\mathrm{\Delta }T\text{(17)}& {\displaystyle }\mathrm{\Delta }T=T_{\mathrm{em}\mathrm{1}}+T_{\mathrm{FH}}+T_{\mathrm{em}\mathrm{2}}\end{array}$$

The motor electromagnetic torque T_e contains the 1st, 2nd, 6th, and 12th harmonics. The presence of these harmonics can cause speed fluctuations, especially when the motor rotates at low speed.

4 The influence of torque harmonics on motor speed for the DDFS

The relationship between the motor output speed ω_e,i, the motor input speed ω ref_e,i ($i=\mathrm{1},\mathrm{2}$), and the disturbance T_L can be obtained by the Laplace transform as shown in the following equation.

$$\begin{array}{}\text{(18)}& {\mathit{\omega }}_{\mathrm{e},i}=H\left(s\right){\mathit{\omega }}_{\mathrm{e}i}^{\mathrm{ref}}-S\left(s\right)T_{\mathrm{L}},\end{array}$$

where H(s) and S(s) are the closed loop transfer function and the sensitivity function, respectively. The expressions of H(s) and S(s) are listed in Appendix A.

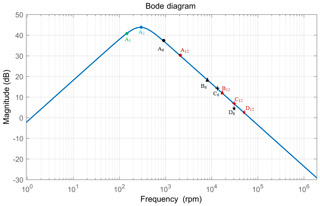
The Bode magnitude plot of S(s) is shown in Fig. 3, in which the horizontal axis represents the electrical angular speed of the PMSM. The torque harmonics are regarded as the disturbance signals. Figure 3 shows that as the electrical angular speed increases, the influence of the torque harmonics on the torque ripple increases first and then decreases. When the DDFS is used, according to the Bode magnitude plot of the S(s), the high-speed operating conditions with less influence of torque harmonics on motor speed fluctuations are selected for the both PMSMs to achieve low velocity of the table through ball screw pair differential synthesis, which can effectively improve velocity smoothness of the table at low velocity compared with the CDFS.

Figure 3 Bode magnitude plot of the S(s) for the DDFS.

The analysis was carried out with an example of the table velocity 2.5 mm s⁻¹. When the CDFS is used, the corresponding motor speed is 30 r min⁻¹ (the electrical angular speed corresponding to the 6th harmonic of the motor is 900 rpm and is marked A6; the electrical angular speed corresponding to the 12th harmonic of the motor is 1800 rpm and is marked A12). In the DDFS, when the nut servo motor speed is 300, 500, and 800 rpm, the electrical angular speed of the 6th harmonic of the nut servo motor is marked B₆, C₆, and D₆, and the electrical angular speed of the 12th harmonic of the nut servo motor is marked B₁₂, C₁₂, and D₁₂, respectively.

The electrical angular frequency corresponding to the above torque harmonics is marked in Fig. 3. Because the screw servo motor speed is only 30 rpm higher than the nut servo motor in the DDFS, the screw servo motor torque harmonics are located near the corresponding torque harmonics of the nut servo motor. It can be seen from Fig. 3 that the Bode magnitude plot of S(s) has better suppression of the harmonic torque of the PMSM for the DDFS at a high speed, and the low velocity of the table is obtained by both motors' synthesis. It can effectively reduce the velocity fluctuation of the table compared with the CDFS.

5 Simulation of the velocity fluctuation for the table

To simulate the velocity fluctuation of the table at low velocity for the DDFS compared with the CDFS, the torque harmonics caused by a non-sinusoidal flux density distribution is simulated by using Eq. (15), in which the 6th and 12th torque components are taken as 6 % and 2 % of the rated torque, respectively (Houari et al., 2015). The velocity ripple factor (VRF) is used to evaluate the velocity fluctuation of the table, which indicates the percentage of the velocity deviating from the reference velocity.

$$\begin{array}{}\text{(19)}& \mathrm{VRF}={\displaystyle \frac{V_{\text{pk-pk}}}{V_{\mathrm{e}}^{\mathrm{ref}}}}\times \mathrm{100}\mathit{\%},\end{array}$$

where V_pk-pk is the peak-to-peak value of the velocity fluctuation for the table and $V_{\mathrm{e}}^{\mathrm{ref}}$ is the reference velocity of the table.

The reference velocity 2.5 mm s⁻¹ of the table is selected for analysis under the load of 1 Nm. Figure 4 shows the velocity fluctuation of the table for the DDFS at different synthesis speeds of both PMSMs compared with the CDFS (the speed of the nut servo motor is 0 mm s⁻¹) when the reference velocity of the table is 2.5 mm s⁻¹. Figure 4a shows the comparison of the table velocity fluctuations of CDFS and DDFS when the nut servo motor speed is 300 rpm in the DDFS. Figure 4b shows the comparison of the table velocity fluctuations of CDFS and DDFS when the nut servo motor speed is 500 rpm in the DDFS. Figure 4c shows the comparison of the table velocity fluctuations of CDFS and DDFS when the nut servo motor speed is 800 rpm in the DDFS.

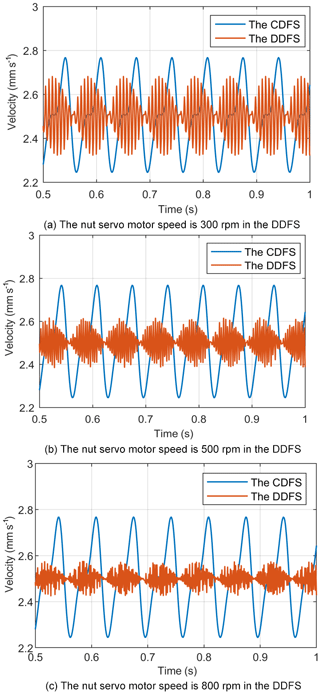
Figure 4 Comparison of the table velocity fluctuations of CDFS and DDFS at 2.5 mm s⁻¹ under 1 N m load torque.

Figure 4 indicates that the two motors can be synthesized at a high speed to obtain a low velocity of the table in the DDFS, which can effectively reduce the velocity fluctuation of the table compared with the CDFS.

Figure 5 Experimental setup device.

Figure 6 Comparison of the table velocity fluctuations of CDFS and DDFS when the nut servo motor speed is 300 rpm in the DDFS.

6 Experiment results validate

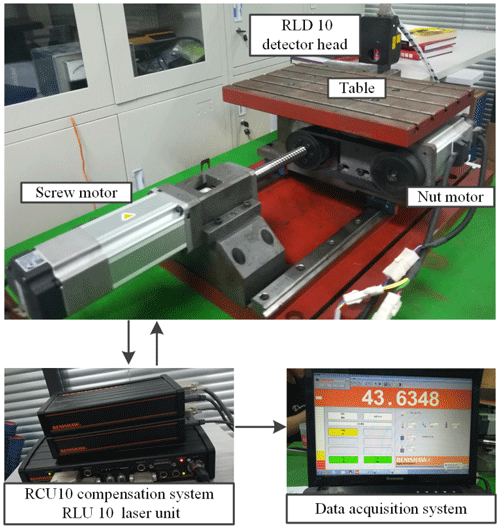
In order to compare the velocity fluctuations at low velocity of the table for the CDFS and the DDFS, the experimental setup device is shown in Fig. 5. The experimental equipment includes the DDFS, Renishaw RLE 10 fiber laser scale (RLD 10 detector head, RLU 10 laser unit, RCU 10 compensation system), and data acquisition system. In the experiments, the sampling frequency of the fiber laser scale is set to 10 kHz.

When the CDFS is used, the speed of the nut servo motor is set to 0 rpm and the table is driven only by the screw servo motor. When the DDFS is used, we make both motors rotate in the same direction at high speed and differentially synthesize by the ball screw pair to obtain low velocity of the table.

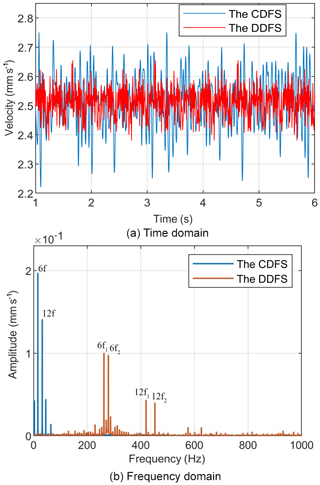
Figure 7 Comparison of the table velocity fluctuations of CDFS and DDFS when the nut servo motor speed is 500 rpm in the DDFS.

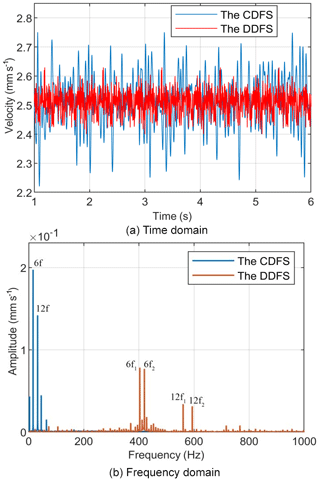
Figure 8 Comparison of the table velocity fluctuations of CDFS and DDFS when the nut servo motor speed is 800 rpm in the DDFS.

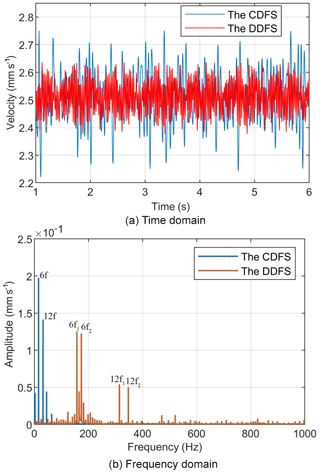
The velocity fluctuations of the table for the DDFS at different synthesis speeds of both PMSMs compared with the CDFS are studied when the reference velocity of the table is 2.5 mm s⁻¹. Figures 6, 7, and 8 show a comparison of the time and harmonic spectrum for the table velocity fluctuations of CDFS and DDFS when the nut servo motor speeds are 300, 500, and 800 rpm in the DDFS, respectively. From Fig. 6 it can be seen that the VRF rates of the table are decreased from 20.1 % with the CDFS to 13.4 % with the DDFS, when the speed of the nut servo motor is 300 rpm in the DDFS. Figure 7 indicates that the VRF rates of the table are decreased from 20.1 % with the CDFS to 10.6 % with the DDFS, when the speed of the nut servo motor is 500 rpm in the DDFS. Figure 8 illustrates that the VRF rates of the table are decreased from 20.1 % with the CDFS to 8.2 % with the DDFS, when the speed of the nut servo motor is 800 rpm in the DDFS.

Figure 9 The VRF rate of the table varies with the speed of the nut servo motor.

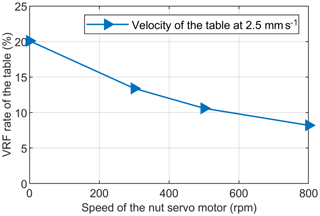
When the velocity of the table is 2.5 mm s⁻¹ in the DDFS, the VRF rate of the table varies with the speed of the nut servo motor as shown in Fig. 9, which indicates that the VRF rate of the table gradually decreases with the increase in the speed of the nut servo motor in the DDFS. Compared with the CDFS, the DDFS can significantly improve the low-velocity smoothness of the table.

7 Conclusion

In this paper, a novel DDFS is developed to reduce the influence of torque harmonics of PMSM on speed fluctuations of a linear feed system at low-speed operation.

Some conclusions can be drawn as follows.

1. The law of the influence of motor torque harmonics on motor speed for the DDFS is analyzed by the sensitivity function of the servo system, which indicates that the torque harmonics have little effect on the motor speed at high-speed operation.

2. According to the law of the influence of motor harmonics on motor speed in the DDFS, we make two motors rotate in the same direction at high speed and differentially synthesize at the ball screw to obtain low-velocity smoothness linear motion.

3. The analysis is carried out with an example of the table velocity 2.5 mm s⁻¹, which indicates that the VRF rate of the table gradually decreases with the increase in the speed of the nut servo motor in the DDFS. Compared with the CDFS, the DDFS can significantly improve the low-velocity smoothness of the table.

Appendix A

The closed loop transfer function H(s) and the sensitivity function S(s) can be expressed as follows:

$$\begin{array}{}\text{(A1)}& {\displaystyle }H\left(s\right)={\mathrm{Num}}_{H\left(s\right)}/\mathrm{Den}\left(s\right),\text{(A2)}& {\displaystyle }S\left(s\right)={\mathrm{Num}}_{S\left(s\right)}/\mathrm{Den}\left(s\right),\text{(A3)}& {\displaystyle }\begin{array}{rl}{\mathrm{Num}}_{H\left(s\right)}& =\left(K_{\mathrm{pc}}{K}_{\mathrm{p}\mathit{\omega }}{\mathit{\psi }}_{\mathrm{f}}{p}^{\mathrm{2}}\right)s^{\mathrm{2}}\\ & +\left(K_{\mathrm{ic}}{K}_{\mathrm{p}\mathit{\omega }}{\mathit{\psi }}_{\mathrm{f}}{p}^{\mathrm{2}}+K_{\mathrm{i}\mathit{\omega }}{K}_{\mathrm{pc}}{\mathit{\psi }}_{\mathrm{f}}{p}^{\mathrm{2}}\right)s\\ & +K_{\mathrm{ic}}{K}_{\mathrm{i}\mathit{\omega }}{\mathit{\psi }}_{\mathrm{f}}{p}^{\mathrm{2}},\end{array}\text{(A4)}& {\displaystyle }{\mathrm{Num}}_{S\left(s\right)}=\left(L_{\mathrm{s}}p\right)s^{\mathrm{3}}+\left(K_{\mathrm{pc}}p+R_{\mathrm{s}}p\right)s^{\mathrm{2}}+\left(K_{\mathrm{ic}}p\right)s,\text{(A5)}& {\displaystyle }\begin{array}{rl}\mathrm{Den}\left(s\right)& =\left(J_{\mathrm{M}}{L}_{\mathrm{s}}\right)s^{\mathrm{4}}+\left(B{L}_{\mathrm{s}}+J_{\mathrm{M}}{K}_{\mathrm{pc}}+J_{\mathrm{M}}{R}_{\mathrm{s}}\right)s^{\mathrm{3}}\\ & +\left(K_{\mathrm{pc}}{K}_{\mathrm{p}\mathit{\omega }}{\mathit{\psi }}_{\mathrm{f}}{p}^{\mathrm{2}}+B{K}_{\mathrm{pc}}+B{R}_{\mathrm{s}}+J_{\mathrm{M}}{K}_{\mathrm{ic}}\right)s^{\mathrm{2}}\\ & +\left(B{K}_{\mathrm{ic}}+K_{\mathrm{ic}}{K}_{\mathrm{p}\mathit{\omega }}{\mathit{\psi }}_{\mathrm{f}}{p}^{\mathrm{2}}+K_{\mathrm{i}\mathit{\omega }}{K}_{\mathrm{pc}}{\mathit{\psi }}_{\mathrm{f}}{p}^{\mathrm{2}}\right)s\\ & +K_{\mathrm{ic}}{K}_{\mathrm{i}\mathit{\omega }}{\mathit{\psi }}_{\mathrm{f}}{p}^{\mathrm{2}}.\end{array}\end{array}$$