the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Dynamic modal analysis of double-sided meshing nutation drive with double circular arc spiral bevel gears
Zheng Lin
Ligang Yao
Zhiyu Xie
In order to reduce the vibration of the double-sided meshing nutation drive with double circular arc spiral bevel gears, the dynamic modal of the nutation system is analyzed. The bending-torsional-axial coupling nonlinear dynamic model of the double-sided meshing nutation drive system with time-varying meshing stiffness, meshing damping, transmission error and tooth backlash is established, and the equation of motion of the system is derived. The natural frequencies and corresponding modal modes of the nutation system are calculated, and the effects of the average meshing stiffness of gears and the bearing support stiffness of nutation gears on the modal of the system are analyzed. The modal analysis of double circular arc spiral bevel gears is carried out, and the ten order natural frequencies and their corresponding modes are obtained. The results show that the nutation drive system and the double circular arc spiral bevel gears do not resonate during transmission.
- Article
(1931 KB) - Full-text XML
- BibTeX
- EndNote
The bevel gear nutation transmission mechanism is a new type of coaxial transmission, which has the advantages of large transmission ratio, simple and compact structure, small volume and large bearing capacity (Lin et al., 2010), and has been widely used in various industrial equipment. Many experts and scholars have designed various types of nutation mechanisms and conducted corresponding research. Gupta and White (1975) studied the kinematics of the nutating mechanical drive and deduced the nutating unbalanced motion equation. Uzuka et al. (2009) designed different nutation motors based on the principle of nutation, including nutation magnetic motor, nutation air motor (Oda et al., 2010), etc., and also analyzing the magnetic field of the nutation magnetic motor (Kadota et al., 2013). Itzhak (2008) performed kinematics and kinetics of rotors and wobbling bodies in nutation drive. Nelson and Cipra (2005) studied the basic principles of nutating mechanisms and analyzed the respective characteristics of nutating gear mechanism and planetary gear mechanism. Huang et al. (2016) designed a novel non-contact nutation drive mechanism, and the experimental analysis was carried out. Fanghella et al. (2015, 2016) studied the kinematics, efficiency and dynamic balancing of planetary gear train based on nutating bevel gears and performed a balanced simulation analysis. Yao et al. (2010) designed a double circular arc spiral bevel gear nutation drive and a non-contact nutation drive mechanism, and derived the calculation formula of the nutation mechanism transmission ratio, and established the tooth surface meshing equations of different tooth profiles (Gu et al., 2006; Lin and Yao, 2012). The influence of machining error and assembly error on the characteristics of the nutation drive had been analyzed (Cai et al., 2017). Then the Mathematical modeling and characteristics analysis for the nutation gear drive based on error parameters had been established (Ji et al., 2016).
The double-sided meshing nutation drive of double circular arc spiral bevel gears is a new transmission system consisting of two pairs of double-arc spiral bevel gears meshed at different sides. External loads, time-varying meshing stiffness and gear tooth error will generate dynamic excitation to the system when working. Under the condition of high speed and heavy load, the system may produce severe vibration and noise. At present, the existing literature mainly studies the structure design, gear meshing analysis and strength analysis of nutation mechanism, while the research on the dynamics of double-sided meshing nutation drive with double-arc spiral bevel gears is rare.
In order to reveal the universal law of the dynamic characteristics of nutation drive system, this paper studies the non-linear dynamic modeling, derivation of equation of motion, system inherent modal and gear modal of double-sided meshing nutation drive system with double circular arc spiral bevel gears.
2.1 Dynamic model
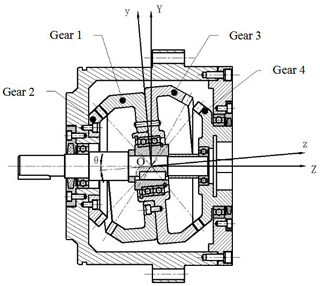
The structure of double-side meshing nutation drive is shown in Fig. 1. It is mainly composed of four double circular arc spiral bevel gears, input horizontal axis and nutation eccentric sleeve. The input horizontal axis and nutation eccentric sleeve are fixed together and the angle θ between the central axis is nutation angle. When the mechanism moves, the motor drives the input horizontal axis and the nutation eccentric sleeve to rotate, thereby driving the internal bevel gears 1 and 3 which are fixed together to perform the nutating motion. The nutation internal bevel gears 1 and 3 are respectively meshed with the fixed external bevel gear 2 and output external bevel gear 4 on the left and right sides, and the power is output by the external bevel gear 4. The double-sided meshing nutation drive can be regarded as a planetary gear transmission with less tooth difference.
In the dynamic modeling of double-sided meshing nutation drive, the system model is simplified to some extent, and the following assumptions are made: (1) The friction of tooth surface during gear meshing is not considered; (2) The system damping is regarded as general viscous damping; (3) The influence of the error between axes on the system is neglected; (4) The deformation of shaft and bearings is not considered, and the bearing clearance is neglected; (5) When nutation gear 1 and nutation gear 3 are fixed together, they are regarded as a whole, gear 1 and gear 3 have the same degree of freedom, the vibration displacement of the two gears is the same, and there is no mutual torsion between the two gears; (6) The torsional pendulum vibration has less influence on the system, ignoring the torsional pendulum vibration.
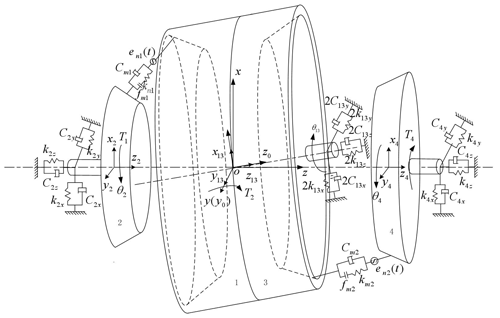
Based on the above assumptions, the bending-torsion-axis coupling analysis model of the double-sided meshing nutation drive system is established by using the lumped parameter method, as shown in Fig. 2. The gears are regarded as lumped mass and lumped inertia, the supporting shaft is regarded as a rigid body without mass, and the elastic support of the bearing is simulated by spring and damper.
In Fig. 2, O–xyz is a space meshing coordinate system, O–x0y0z0 is a follow-up coordinate system which rotates with nutation gears 1 and 3. The origins of the two coordinate systems coincide with the conical points of each bevel gear. T1 and T4 are input torque and load torque respectively. xi, yi and zi are the translational vibration displacements of the gears in the x, y and z directions respectively. The subscript i=13, 2, 4 respectively represent the nutation gears 1 and 3, fixed external bevel gear 2 and output external bevel gear 4. θi is the angular vibration displacement of each gear in the z direction. kik and Cik (i=13, 2, 4; k=x, y, z) are the support stiffness and support damping of each gear in three coordinate directions respectively. kmj, Cmj and enj(t) are the meshing stiffness, meshing damping and static transmission error of each gear pair. The subscript j=1, 2 respectively denote the gear pair 1 which is meshed by the fixed bevel gear 2 and the nutation bevel gear 1, and the gear pair 2 which is meshed by the output bevel gear 4 and the nutation bevel gear 3.
The generalized displacement array of the double-sided nutation drive system can be expressed as:
2.2 Equation of motion
The relative displacements λn1 and λn2 along the normal direction of the meshing point due to vibration and error between the meshing points of the two bevel gears in the gear pairs 1 and 2 are represented as:
In Eqs. (2) and (3),
where, δi (i=1, 2, 3, 4) is the pitch cone angle of each bevel gear, β is the helical angle, αn is the normal pressure angle, rmi (i=1, 2, 3, 4) is the radius at the meshing point of each gear.
The normal dynamic load of gear pair in meshing can be expressed as,
where, j=1, 2 represent the gear pairs 1 and 2, kmj(t) represent time-varying meshing stiffness of gear pairs, f(λnj) represent clearance function.
The clearance function is as follows:
where, bj (j=1, 2) is the tooth backlash of each gear pair.
Considering the time-varying meshing stiffness, transmission error, meshing damping and tooth backlash, the dynamic differential equations of double-sided meshing nutation drive system are obtained as,
where, mi and Ji (i=13, 2, 4) are the lumped mass and moment of inertia of each gear; L1 and L3 are the gyroscopic moments generated by nutation motion of two nutation bevel gears, and the direction is along the axis O–y.
2.3 Meshing stiffness analysis
In the meshing process of double circular arc spiral bevel gears, meshing stiffness varies with the number of meshing points of convex and concave teeth, and the meshing stiffness has time-varying. By using the finite element contact analysis, the contact force and deformation of the gear teeth in the meshing period are obtained. Then the meshing stiffness values of gear pairs at different times are calculated, and these discrete points are connected by straight lines, as shown in Fig. 3.
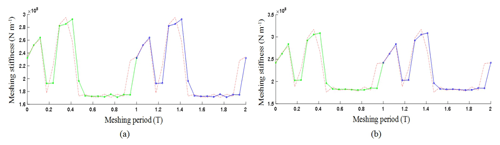
Figure 3Fitting curve of time-varying meshing stiffness. (a) Meshing stiffness of the gear pair 1. (b) Meshing stiffness of the gear pair 2.
In order to transform the time-varying meshing stiffness broken line into a continuous function curve with time as independent variable, the time-varying meshing stiffness kmj(t) is fitted into Fourier progression form.
where, kmj is the average meshing stiffness of the gear pair, r (r=1, 2, …, l) is the order of Fourier expansion harmonic term, krj is the stiffness amplitude of the r order harmonic component of the gear pair, ωmj is the meshing angular frequency, φrj is the meshing phase of the r order harmonic component.
To simplify the calculation, the curve of time-varying meshing stiffness is obtained by fitting the 7th order Fourier progression as shown by the red dotted line in Fig. 3. And the average meshing stiffness of the gear pair 1 is calculated as N m−1, and the average meshing stiffness of the gear pair 2 is N m−1.
3.1 Inherent characteristics of system
Theoretical modal analysis solves the inherent characteristics of the system, i.e. the natural frequency and the modal shape. Therefore, the influence of external loads can be neglected, and the damping term can also be neglected because the influence of damping is small. Thus, the free equation of motion of double-sided meshing nutation drive can be established.
where, the mass matrix M=diag (m2, m2, m2, J2, m13, m13, m13, J13, m4, m4, m4, J4), the stiffness matrix K is a 12 by 12 matrix, which is not listed in the text due to limited space.
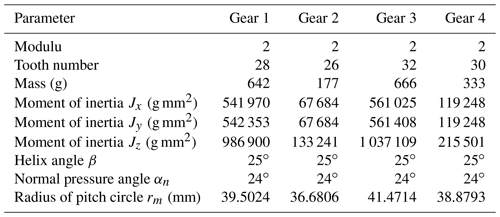
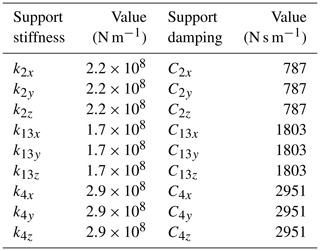
The intrinsic characteristics of the nutation drive system are solved in the MATLAB software, and the eig command is used to solve the problem. In solving the free equation of motion of nutation drive system, the average meshing stiffness of two pairs of gears is used to calculate the natural frequencies and modal shapes of nutation drive system. The parameters of bevel gears of nutation drive solved in this paper are shown in Table 1. The values of support stiffness and support damping of nutation drive system are shown in Table 2.
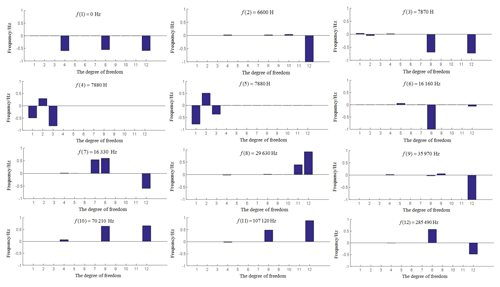
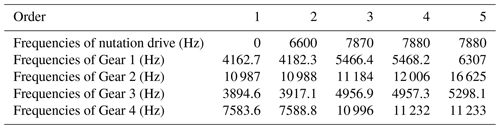
The natural frequencies of the double-sided meshing nutation drive are calculated as shown in Table 3, and the corresponding modal shapes are shown in Fig. 4. The degrees of freedom 1 to 4 are the degrees of freedom of the fixed external bevel gear 2, the degrees of freedom of 5 to 8 are the degrees of freedom of the nutation bevel gears 1 and 3, and the degrees of freedom of 9 to 12 are the degrees of freedom of the output external bevel gear 4. The natural frequency of the first 5th order of the nutation drive system is small, the natural frequency after the sixth stage is large, and the natural frequencies span of the system is also large. In general, the natural frequencies of the first to tenth order have a greater impact on the system. There is a natural frequency double root solution in the system, that is, the natural frequency values of the 4th and 5th order both are 7880 Hz.
3.2 Influence of meshing stiffness and bearing support stiffness on modal
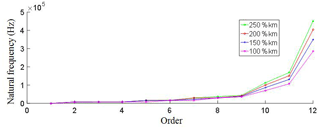
In order to analyze the influence of meshing stiffness on modal, the natural frequencies of nutation drive system are calculated by taking the average meshing stiffness of two pairs of gears as 150 %, 200 % and 250 % of the original average meshing stiffness kmj (j=1, 2). The natural frequencies of nutation system with different average meshing stiffness are shown in Fig. 5.
Figure 5 shows that the average meshing stiffness has a great influence on the high order natural frequencies, and mainly affects the natural frequencies of the 10th, 11th and 12th order. The average meshing stiffness has little effect on the lower order, only the natural frequencies of the 5th and 7th order increase slightly. The lower order of natural frequencies have great influence on the system, so the change of average meshing stiffness has little influence on the nutation drive system.
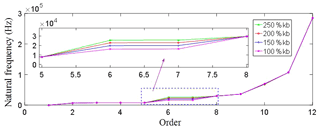
Considering that there are two nutation gears in nutation drive system to make the nutation movement, the natural frequencies of nutation drive system are calculated by taking the bearing support stiffness of nutation gears as 150 %, 200 % and 250 % of the original support stiffness. The comparison of natural frequencies of nutation system under different bearing supporting stiffness of nutation gears is shown in Fig. 6.
It can be seen from Fig. 6 that the bearing support stiffness of nutation gears has a great influence on the natural frequency of intermediate order, especially on the sixth and seventh order. However, the bearing support stiffness of the nutation gears has little influence on the low-order and high-order, and the natural frequencies of the 10th to 12th order remain unchanged with different bearing supporting stiffness of nutation gears.
Using ANSYS Workbench software to analyze the modal of double circular arc spiral bevel gears, the first ten natural frequencies and corresponding vibration modes of double circular arc spiral bevel gears can be obtained. In this paper, the material of double circular arc spiral bevel gear is set as structural steel, elastic modulus E is 206 GPa, Poisson's ratio is 0.29, mass density is 7850 kg m−3. The mesh models of double circular arc spiral bevel gears 1 and 2 are shown in Fig. 7.
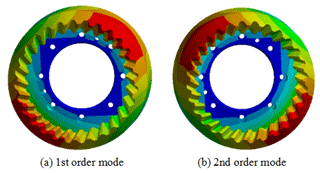
By setting the order of modal solution and solving the modal of bevel gears, the vibration mode diagrams of double circular arc spiral bevel gears can be obtained. Taking the vibration mode diagram of internal bevel gear 1 as the example, the 1st and 2nd order modes are torsional vibration, and the end face of bevel gear oscillates back and forth along the radial straight line passing through the axis, as shown in Fig. 8.
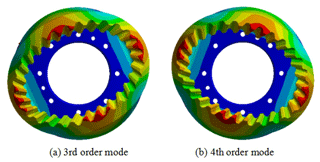
The 3rd and 4th order modes of the internal bevel gear 1 are folding vibration. The bevel gear 1 appears as V-shaped along the axis, and the regular polygon on the end face, as shown in Fig. 9.
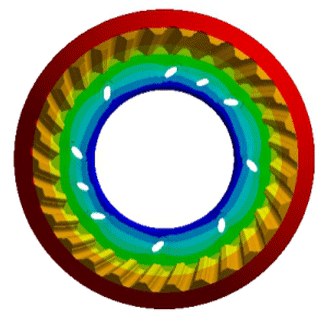
The 5th order mode of the internal bevel gear 1 is an umbrella type vibration, and the bevel gear teeth are contracted into an umbrella shape along the large end in the axial direction, as shown in Fig. 10.
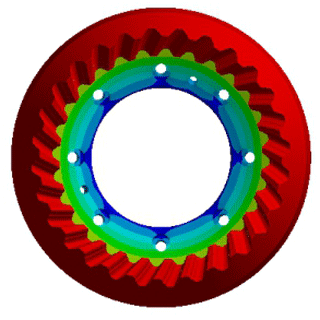
The 6th order mode of the internal bevel gear 1 is a circumferential vibration, as shown in Fig. 11. The bevel gear has substantially no vibration and displacement in the axial direction, and a circumferential vibration on the end face.
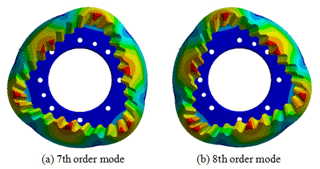
The 7th and 8th order modes of the internal bevel gear 1 are bending vibration. The regular wave pattern appears in the axial direction of the gear, and the regular polygon appears on the end face, as shown in Fig. 12.
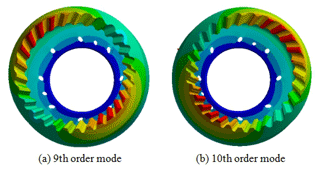
The 9th and 10th order modes of internal bevel gear 1 are radial vibration, as shown in Fig. 13. The bevel gear expands and contracts along the radial direction. The end face appears elliptical mode of vibration, and there is basically no vibration in the axial direction.
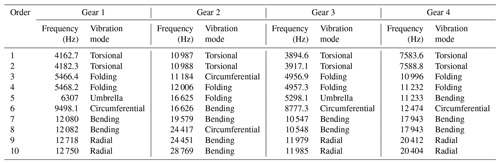
The natural frequencies and vibration modes of four bevel gears are obtained as shown in Table 4. It can be seen from Table 4 that the first and second order modes of the four bevel gears are torsional vibration, the intermediate-order modes are umbrella type vibration, folding vibration and circumferential vibration, and the high-order modes is bending vibration and radial vibration. When the frequencies of adjacent orders of the same gear are similar, the vibration modes are basically the same.
At low-order (1–5th order), the comparison between the natural frequency of nutation drive system obtained by numerical solution and the natural frequencies of four bevel gears obtained by finite element analysis is shown in Table 5. The natural frequencies of bevel gears 1 and 3 are smaller than those of bevel gears 2 and 4, and the natural frequencies of bevel gears 2 are the largest. Because gears 1 and 3 are connected together and the structural parameter values of gears are close, the increasing law of natural frequencies of each order is similar. At the same time, it can be seen from table 5 that the low-order natural frequencies of the four bevel gears are different from the natural frequencies of the nutation drive system, so the double-sided meshing nutation drive with double circular arc spiral bevel gears generally does not produce resonance.
The bending-torsional-axial coupling nonlinear dynamic model of double-sided meshing nutation drive system has been established, which includes time-varying meshing stiffness, meshing damping, transmission error, tooth clearance and other factors. And then the equation of motion of the double-sided meshing nutation drive system is derived.
The natural frequencies and corresponding modal modes of the nutation drive system are calculated according to the free equation of motion. The influence of the meshing stiffness and bearing support stiffness of nutation gears on the modal of nutation drive are analyzed. The results show that the average meshing stiffness mainly affects the high-order natural frequencies of nutation drive system, while the bearing support stiffness of nutation gears mainly affects the low-order natural frequencies of nutation drive system.
The modal analysis of the double circular spiral bevel gear is carried out, and the first ten natural frequencies of the double circular spiral bevel gear and their corresponding vibration modes are obtained. The natural frequencies of nutation drive system and double circular arc spiral bevel gears are different, and there is no resonance.
All data included in this study are available upon request by contact with the corresponding author.
LY proposed the idea and methodology. ZL and ZX applied the methodology, performed analytical solutions. ZL surveyed the literature and wrote the paper.
The authors declare that they have no conflict of interest.
This research has been supported by the National Natural Science Foundation of China (grant no. 51775114), the Fujian Provincial Industrial Robot Basic Components Technology Research and Development Center (grant no. 2014H21010011), and the Fujian Provincial Young and Middle-aged Teacher Education and Scientific Research (grant nos. JAT160510 and JAT190777).
This paper was edited by Ali Konuralp and reviewed by two anonymous referees.
Cai, Y. W., Yao, L. G., Xie, Z. Y., and Zhang, J.: Influence analysis of system parameters on characteristics of the nutation drive with double circular arc spiral bevel gears, Forsch. Ingenieurwes., 81, 125–133, https://doi.org/10.1007/s10010-017-0245-x, 2017.
Fanghella, P., Bruzzone, L., and Ellero, S.: Dynamic balancing of a nutating planetary bevel gear train, Mech. Mach. Sci., 25, 23–33, https://doi.org/10.1007/978-3-319-09858-6_3, 2015.
Fanghella, P., Bruzzone, L., and Ellero, S.: Kinematics, efficiency and dynamic balancing of a planetary gear train based on nutating bevel gears, Mech. Based Des. Struc., 44, 72–85, https://doi.org/10.1080/15397734.2015.1047956, 2016.
Gu, B., Yao, L. G., Wei, G. W., Cai, Y. J., and Dai, J. S.: The analysis and modeling for nutation drives with double circular-arc helical bevel gears, Mater. Sci. Forum, 505–507, 949–954, https://doi.org/10.4028/www.scientific.net/MSF.505-507.949, 2006.
Gupta, P. K. and White, H. V.: On the kinematics of a nutating mechanical drive, J. Appl. Mech, 42, 507–509, https://doi.org/10.1115/1.3423617, 1975.
Huang, D. J., Ding, S. H., Su, X. L., Qiu, J. W., Liu, Z. W., Shi, L. S., and Yao, L. G.: Design and experimental analysis for a novel non-contact nutation drive mechanism, Journal of Fujian University of Technology, 14, 51–54, https://doi.org/10.3969/j.issn.1672-4348.2016.01.012, 2016.
Itzhak, G.: On the kinematics and kinetics of mechanical seals, rotors, and wobbling bodies, Mech. Mach. Theory, 43, 909–917, https://doi.org/10.1016/j.mechmachtheory.2007.06.004, 2008.
Ji, W. T., Yao, L. G., and Zhang, J.: Mathematical modeling and characteristics analysis for the nutation gear drive based on error parameters, J. Chongqing Univ. Eng. Ed., 15, 149–158, https://doi.org/10.11835/j.issn.1671-8224.2016.04.003, 2016.
Kadota, Y., Inoue, K., Uzuka, K., Suenaga, H., and Morita, T.: Noncontact operation of a miniature cycloid motor by magnetic force, IEEE-ASME T. Mech., 18, 1563–1571, https://doi.org/10.1109/TMECH.2012.2208225, 2013.
Lin, Z. and Yao, L. G.: General mathematical model of internal meshing spiral bevel gears for nutation drive, Appl. Mech. Mater., 101–102, 708–712, https://doi.org/10.4028/www.scientific.net/AMM.101-102.708, 2012.
Lin, Z., Yao, L. G., and Huang, S. J.: Transmission ratio analysis and controllable tooth profile modeling for the nutation drive with double circular-arc external and internal spiral bevel gears, Adv. Mat. Res., 97–101, 3128–3134, https://doi.org/10.4028/www.scientific.net/AMR.97-101.3128, 2010.
Nelson, C. A. and Cipra, R. J.: Similarity and equivalence of nutating mechanisms to bevel epicyclic gear trains for modeling and analysis, J. Mech. Design, 127, 269–277, https://doi.org/10.1115/1.1829068, 2005.
Oda, S., Suzumori, K., Uzuka, K., and Enomoto, I.: Development of nutation motors (improvement of pneumatic nutation motor by optimizing diaphragm design), J. Mech. Sci. Technol., 24, 25–28, https://doi.org/10.1007/s12206-009-1157-y, 2010.
Uzuka, K., Enomoto, I., and Suzumori, K.: Comparative assessment of several nutation Motor Types, IEEE-ASME T. Mech., 14, 82–92, https://doi.org/10.1109/TMECH.2008.2004035, 2009.
Yao, L. G., Gu, B., Huang, S. J., Wei, G. W., and Dai, J. S.: Mathematical modeling and simulation of the external and internal double circular-arc spiral bevel gears for the nutation drive, J. Mech. Design, 132, 021008, https://doi.org/10.1115/1.4001003, 2010.