Design of experiment-based tolerance synthesis for a lock-or-release mechanism of the Chinese Space Station Microgravity Platform

This paper deals with the tolerance synthesis with the application for a typical Lock-or-Release (L/R) mechanism, used for Chinese Space Station Microgravity Platform (SSMP). The L/R mechanism is utilized to lock the SSMP maintaining space position during the launching stage, and to release the SSMP automatically during on-orbit stage. Manufacturing accuracy of L/R mechanism presents direct influence on its kinematic and dynamic behaviors. Tolerance synthesis can provide a reasonable assignment of tolerance, satisfying the critical assembly criteria while lowering manufacturing complexity. In this paper, based on the number-theory method (NTM), a Halton-set based Monte Carlo (MC) simulation is introduced in the accuracy model of the L/R mechanism, aiming at improving analytical precision and efficiency for tolerance synthesis. A design of experiment (DOE) based tolerance synthesis approach is proposed. With initial tolerance determined by capacity, sensitivities of different tolerance factors are generated through the first DOE stage, and then applied to determine feasible tolerance levels. The final tolerance assignments, like points scatted in high-dimensioned space with inherent uniformity, are then produced through uniform DOE in the second stage. Result shows that the majority of feasible tolerance assignments generated have more relaxed tolerance, which can facilitate the manufacturing process.

1 Introduction

As one of scientific exploration oriented carriers, the Chinese Space Station Microgravity Platform (SSMP) provides a higher level of controllable environment for samples and instruments and facilitates delicate manipulations in diverse new technology experiments, such as material sciences, microgravity fluid physics and biotechnology (Xie et al., 2016; Wang et al., 2014; Liu et al., 2006). The L/R mechanism is configured in parallel, developed and equipped supportively for the SSMP, and its hierarchical relation is illustrated in Fig. 1. The conceptual model of the Chinese Space Station, consists of a core chamber module and four experimental chamber modules. In each experimental module, each scientific research experiment rack is fixed in parallel with the others (Zhou, 2013; Liu et al., 2014). Two auto L/R mechanisms are assembled into both sides of each scientific research experiment rack to lock the SSMP. During the shuttle launching stage, the SSMP is securely locked by eight lead screws of the L/R mechanisms on both sides. While arriving at the scheduled orbit of the space station, the lead screws on each side are driven inversely to release the SSMP for microgravity experiments.

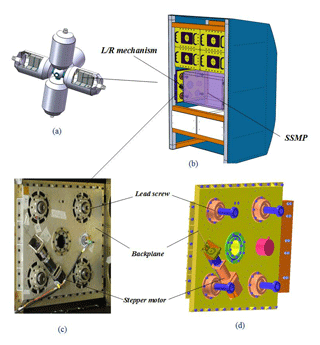
Figure 1 Hierarchical relation (a) conceptual model of the Chinese Space Station; (b) scientific research experimental rack and the SSMP with two L/R mechanisms in a locked status; (c) physical prototype and (d) 3-D model of the L/R mechanism on a side of the SSMP.

Manufacturing accuracy is critical to the kinematic and dynamic performance of the L/R mechanism (Ding et al., 2018). Nowadays, lower consumption and higher performance have been always pursued for all manufacturing companies, particularly considering the current context of increasing global competition. Tolerance assignments for mechanical parts and assembly of a product play an important role in the accuracy performance of the product, since it is closely connected with components' tolerance (Merlet, 2006; Hao and Kong, 2016; Hao and Merlet, 2005; Huang et al., 2016; Huang and Kong, 2010; Li et al., 2016). As one of the crucial tasks in a product life cycle, tolerance synthesis for mechanical parts and assembly of a product, which is generally regarded as tolerance design, is a typical iterative procedure. It ranges from tolerance initialization to final reasonable tolerance determination, in which constraints such as manufacturing capability, performance quality and production cost are considered (Moroni and Polini, 2003; Pasupathy et al., 2003). There are two problems to be addressed: (a) how the mechanism tolerance is assigned, so that manufacturing complexity is reduced without much loss in quality (Singh et al., 2009a; Chen and Ji, 2005; Chlebus and Wojciechowska, 2016; Jeang, 2001; Lyu et al., 2006; Rout and Mittal, 2006, 2007, 2008; Li et al., 2015); and (b) how the synthesis approach is devised so that process data can be promoted in precision and efficiency (Singh et al., 2009b; Huang, 2013).

1.1 Mechanism tolerance synthesis review

Parallel-type mechanisms (Merlet, 2006; Hao and Kong, 2016; Hao and Merlet, 2005) are analogous to the L/R mechanism in structure. Huang et al. (2016) proposed a comprehensive methodology for a 4-degrees-of-freedom (DOF) high-speed pick-place parallel robot with an articulated travelling plate, where the tolerance model for the tilt angular error was established statistically. A strategy was to minimize the total cost while satisfying the permitted angular error and manufacturing feasibility constraints, and a reasonable angular accuracy within cylindrical task workspace is finally generated. Wang and McCarthy (2018) designed a four-bar function generator to act as a flapping wing mechanism. The tolerance zones were specified around the accuracy points, and twenty-nine designs were found to achieve the desired coordination of wing's swing and pitch. Yin et al. (2018) investigated tolerance design for spatial mechanisms with the use of both the extremum and the probability methods. In comparison with several surrogate models, the tolerance was optimized and thus manufacturing cost is significantly reduced.

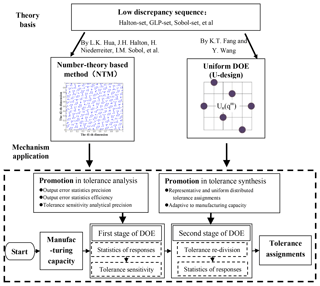
DOE based tolerance design has drawn close attention in recent years for engineering applications. Employing the concept of Taguchi S/N ratio, Rout and Mittal (2006, 2007, 2008) utilized the inner and outer orthogonal array to identify significant parameters of a 2-DOF planar manipulator with two revolute joints for optimum tolerance. Optimum tolerance of the manipulator with payload was finally allocated, and was validated by Monte Carlo (MC) simulation. Huang (2015) developed a Taguchi based optimum tolerance design for a function generation mechanism with joint clearance, where the total cost of assembly was minimized while satisfying the accuracy requirements. Insight on parameter variances of this mechanism was provided with the sensitive maps, and the efficiency and practicality were demonstrated with the proposed method. Li et al. (2015) investigated the tolerance design problem of a 6-DOF space docking mechanism using uniform design, and concerned the efficiency and precision of MC simulation in DOE. The tolerance of the component in the mechanism was properly broadened without any loss of output accuracy, and the manufacturing cost was reduced to a certain extent. Huang (2004, 2013), Huang and Kong (2010) and Zhou (2001) made a comprehensive introduction to the advantages of number-theoretic method (NTM), and exhibited the significant precision and surprising efficiency of NTM in tolerance design and process simulation, which made the comprehensive theory of NTM start to serve the manufacturing in engineering.

1.2 DOE based tolerance synthesis methodology

In a process for mechanism manufacturing, the capacity is constantly influenced by multiple stochastic factors, and presents fluctuant. The tolerance assigned may not be possibly dynamically suitable in practice. Therefore, tolerance assignment should be with the characteristics of redundancy and flexibility. Tolerance synthesis approach should have high analytical precision and efficiency, and generate tolerance assignments with completeness and representativeness, that could be actively resistant to potential failure, due to instability of manufacturing capability.

NTM offers a possible solution for this problem. The essence of NTM is to determine a point-set in a s-dimensioned super-cube, where the points in the set are uniformly distributed (Fang and Wang, 1994). Till now mathematicians have proposed several types of set such as Hua–Wang set (Hua and Wang, 1972), Halton set (Halton, 1960; Chi et al., 2005), Niederreiter set (Niederreiter, 1992) and Sobol set (Sobol, 1967; Bratley and Fox, 1988). They are all termed as low discrepancy sequence (LDS). The initial target of LDS aims at improving MC simulation performances, which are prevailing over the traditional pseudo-random set, then the LDS is introduced in the field of DOE, and as the basis, uniform DOE is established (Fang and Wang, 1994) with GLP-set (Hua and Wang, 1972). Uniform DOE pays more attention on distributional uniformity other than symmetrical comparability of experiment points. It could disclose system information with the fewest representative points. On the contrary, the experiment points construct an optimum and uniform coverage of experiment space.

With this advantage, the uniform DOE array, composed of different levels of tolerance in a mechanism, could construct plenty of candidate tolerance assignments. They are optimally and uniformly distributed within the experiment space. As manufacturing capability fluctuates, these assignments can be valuable and robustly adapt to variation of manufacturing capability.

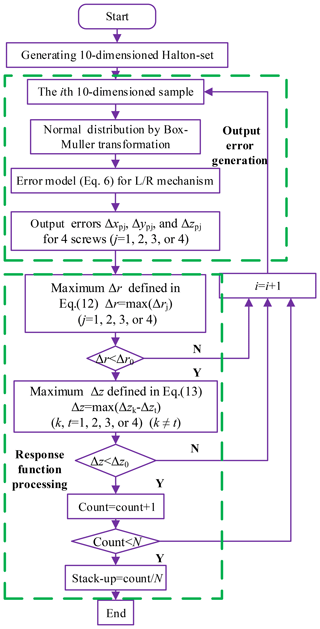
In this paper, the accuracy model for the L/R mechanism is established firstly. For a precise and efficient simulation process, the Halton-set based MC simulation, is introduced in tolerance analysis of the L/R mechanism. Then, tolerance synthesis is proposed consisting of two stages. The first stage of DOE, provides tolerance sensitivity, and the second one, applies uniform DOE to generate tolerance assignments with representativeness and uniformity, against capacity instability and manufacturing complexity. The flowchart of the tolerance synthesis applying both NTM and uniform DOE is illustrated in Fig. 2.

Building on the above advances, this paper focuses on tolerance analysis and synthesis towards application in the L/R mechanism. The reminder of this article is organized as follows: Sect. 2 briefly introduces the structure and principle of the L/R mechanism; Sect. 3 completes accuracy modeling for the L/R mechanism, and conducts tolerance analysis with Halton-set based MC simulation; Sect. 4 details the tolerance synthesis procedures for the L/R mechanism and illustrates the practicability for a case study; Conclusions are drawn in Sect. 5.

Figure 2 Flowchart of tolerance synthesis with both NTM and uniform DOE.

2 L/R mechanism description

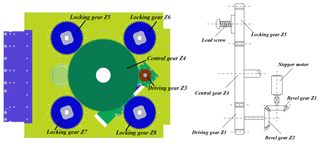
The architecture of a L/R mechanism is illustrated in Fig. 3. The stepper motor on the backside, drives the bevel gear Z1, then revolve gears Z2 and Z3 that are connected together. Driven by a central gear Z4, four branches of gears rotate simultaneously, making four lead screws move forward as synchronous as possible for the locking gears Z5, Z6, Z7, and Z8. The SSMP is securely locked by contacting the ends of the four lead screws, with the slots on both sides of the SSMP. While arriving at scheduled orbit, four lead screws on each side are then driven inversely to release the SSMP.

The L/R mechanism with imperfect manufacturing quality results in two problems: firstly, inaccurate location and transmission of any lead screw would cause the contact backlash between the SSMP and each lead screw. It tends to raise impact damage structurally by harmonic response of the SSMP's vibration during the launch stage; Secondly, the unbalanced locking supports on the SSMP inversely make lead screws unable to form symmetric or regular deformation, which also poses a potential threat to the shuttle structurally. However, higher manufacturing accuracy for the L/R mechanism would inevitably increase manufacturing complexity; it may be unreachable to manufacturing capability. Therefore, an optimum compromise between tolerance and capacity for the mechanism is essential to vouch the system's high reliability and security.

3 Modelling and simulation

Geometrical errors of the L/R mechanism come from the uncertainty of connected components' position and orientation during the manufacturing stages, and complicate the influence of the output errors, which are represented by the end errors of the lead screws. In this section, an accuracy model of the L/R mechanism using vector differential algorithms is established, which provides linear relations between geometrical errors and output errors. On improving accuracy simulation precision and efficiency, the Halton-set based MC simulation is introduced and compared to the traditional pseudo-random set based MC simulation.

Figure 3 Configuration of transmission train of the L/R mechanism.

3.1 Mechanism accuracy modeling

Both the L/R mechanisms are symmetrically configured on both sides of the SSMP as shown in Fig. 1. Each side can provide enough geometric information for accuracy analysis. Four lead screws are fixed on the backplane of the L/R mechanism, and they are guided by a gear train to synchronously travel forward until their ends contact slots of the SSMP on a side.

The imperfectness of assembly generates locational errors δx_p, δy_p, δz_p, δα, δβ and δγof the backplane, they are with respect to the nominal position of the scientific research experiment rack; similarly, each lead screw on the backplane has locational errors δa_i,x, δa_i,y, δa_i,z, and angular errors δu_i,x and δu_i,y about x and y axes. The axial error δl of each lead screw is theoretically contributed by transmission errors from the engaged gears and assembly error. However, repetitive experiments had indicated the axial error of lead screw assembled weighted majority among the translation errors, therefore, the transmission errors are not included in the mechanism accuracy model. The output errors δb_i,x, δb_i,y and δb_i,z refer to inaccuracy between the end of each lead screw and nominal contact center on a side of the SSMP.

Frames {O_B} and $\mathit{\left\{}{O}_{A^{\prime }}\mathit{\right\}}$ attaching at the nominal centers on a surface of the SSMP and mechanism's backplane, are outlined in Fig. 4 respectively. Frame $\mathit{\left\{}{O}_{A^{\prime }}\mathit{\right\}}$ has a positional error vector δp (δx_p, δy_p, δz_p)^T and an angular error vector δΩ (δα, δβ, δγ)^T with respect to the base frame {O_B} . Four lead screws in both coordinate frames form four closed kinematic loops. Since all the lead screws are centrosymmetric about the z^′ axis of coordinate frame $\mathit{\left\{}{O}_{A^{\prime }}\mathit{\right\}}$ , either closed-loop kinematic chain is established independently and representatively.

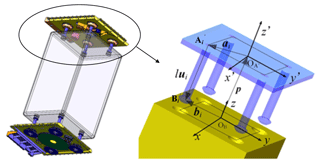
Figure 4 Assembled L/R mechanism with the SSMP and kinematic diagram for this simplified L/R mechanism.

In Fig. 4, the closed-loop kinematic chain $O_B-O_{A^{\prime }}-A_i^{\prime }-B_i^{\prime }$ can be expressed with a vector equation as

$$\begin{array}{}\text{(1)}& {\displaystyle }{\mathit{b}}_i=\mathit{p}+\mathbf{R}\left({\mathit{a}}_i+l_i{\mathit{u}}_i\right)(i=\mathrm{1},\mathrm{2},\mathrm{3}\text{or}\mathrm{4})\end{array}$$

where R refers to the rotational matrix of frame $\mathit{\left\{}{O}_{A^{\prime }}\mathit{\right\}}$ with nominal orientation angles α, β and γ, about x, y and z axes, and can be written as

$$\begin{array}{rl}\mathbf{R}=& \left[\begin{array}{ccc}\cos \mathit{\gamma }& -\sin \mathit{\gamma }& \mathrm{0}\\ \sin \mathit{\gamma }& \cos \mathit{\gamma }& \mathrm{0}\\ \mathrm{0}& \mathrm{0}& \mathrm{1}\end{array}\right]\left[\begin{array}{ccc}\cos \mathit{\beta }& \mathrm{0}& \sin \mathit{\beta }\\ \mathrm{0}& \mathrm{1}& \mathrm{0}\\ -\sin \mathit{\beta }& \mathrm{0}& \cos \mathit{\beta }\end{array}\right]\\ & \left[\begin{array}{ccc}\mathrm{1}& \mathrm{0}& \mathrm{0}\\ \mathrm{0}& \cos \mathit{\alpha }& -\sin \mathit{\alpha }\\ \mathrm{0}& \sin \mathit{\alpha }& \cos \mathit{\alpha }\end{array}\right]\end{array}$$

Differentiating both sides of Eq. (1) yields

$$\begin{array}{}\text{(2)}& \mathit{\delta }{\mathit{b}}_i=\mathit{\delta }\mathit{p}+\mathit{\delta }R\left({\mathit{a}}_i+l_i\cdot {\mathit{u}}_i\right)+R\left(\mathit{\delta }{\mathit{a}}_i+\mathit{\delta }{l}_i\cdot {\mathit{u}}_i+l_i\cdot \mathit{\delta }{\mathit{u}}_i\right)\end{array}$$

where δb_i (δb_i,x, δb_i,y, δb_i,z) denotes the end error vector of theith lead screw in frame {O_B} ; δp(δx_p, δy_p, δz_p)^T refers to the positional error vector of the backplane with respect to base frame {O_B}; δR denotes perturbation of the rotational matrix R of frame $\mathit{\left\{}{O}_{A^{\prime }}\mathit{\right\}}$ with regard to the base frame {O_B}; u_i (u_x, u_y, u_z)^T refers to the unit vector of the ith lead screw; δu_i represents a deviation of u_i, and can be expressed as

$$\begin{array}{}\text{(3)}& \mathit{\delta }{\mathit{u}}_i={\mathrm{\Delta }}_{u_i}{\mathit{u}}_i=\left[\begin{array}{ccc}\mathrm{0}& -\mathit{\delta }{\mathit{u}}_z& \mathit{\delta }{\mathit{u}}_y\\ \mathit{\delta }{\mathit{u}}_z& \mathrm{0}& -\mathit{\delta }{\mathit{u}}_x\\ -\mathit{\delta }{\mathit{u}}_y& \mathit{\delta }{\mathit{u}}_x& \mathrm{0}\end{array}\right]\left[\begin{array}{c}{\mathit{u}}_x\\ {\mathit{u}}_y\\ {\mathit{u}}_z\end{array}\right]\end{array}$$

where ${\mathrm{\Delta }}_{{\mathit{u}}_i}$ denotes the antisymmetric tensor of δu_i.

δR in Eq. (2), has to deal with the perturbation vector δΩ (δΩ_x, δΩ_y, δΩ_z)^T of the nominal angles α, β, and γ, with respect to base frame {O_B} . Therefore, δΩ can be detailed as

$$\begin{array}{rl}\mathit{\delta }\mathbf{\Omega }& =\mathit{\delta }\mathit{\gamma }\left[\begin{array}{c}\mathrm{0}\\ \mathrm{0}\\ \mathrm{1}\end{array}\right]+\mathit{\delta }\mathit{\beta }\left[\begin{array}{ccc}\cos \mathit{\gamma }& -\sin \mathit{\gamma }& \mathrm{0}\\ \sin \mathit{\gamma }& \cos \mathit{\gamma }& \mathrm{0}\\ \mathrm{0}& \mathrm{0}& \mathrm{1}\end{array}\right]\left[\begin{array}{c}\mathrm{0}\\ \mathrm{1}\\ \mathrm{0}\end{array}\right]\\ & +\mathit{\delta }\mathit{\alpha }\left[\begin{array}{ccc}\cos \mathit{\gamma }& -\sin \mathit{\gamma }& \mathrm{0}\\ \sin \mathit{\gamma }& \cos \mathit{\gamma }& \mathrm{0}\\ \mathrm{0}& \mathrm{0}& \mathrm{1}\end{array}\right]\left[\begin{array}{ccc}\cos \mathit{\beta }& \mathrm{0}& \sin \mathit{\beta }\\ \mathrm{0}& \mathrm{1}& \mathrm{0}\\ -\sin \mathit{\beta }& \mathrm{0}& \cos \mathit{\beta }\end{array}\right]\left[\begin{array}{c}\mathrm{1}\\ \mathrm{0}\\ \mathrm{0}\end{array}\right]\end{array}$$

$$\mathit{\delta }\mathbf{\Omega }=\left[\begin{array}{c}\mathit{\delta }{\mathrm{\Omega }}_x\\ \mathit{\delta }{\mathrm{\Omega }}_y\\ \mathit{\delta }{\mathrm{\Omega }}_z\end{array}\right]=\left[\begin{array}{c}-\sin \mathit{\gamma }\mathit{\delta }\mathit{\beta }+\cos \mathit{\gamma }\cos \mathit{\beta }\mathit{\delta }\mathit{\alpha }\\ \cos \mathit{\gamma }\mathit{\delta }\mathit{\beta }+\sin \mathit{\gamma }\cos \mathit{\beta }\mathit{\delta }\mathit{\alpha }\\ -\sin \mathit{\beta }\mathit{\delta }\mathit{\alpha }+\mathit{\delta }\mathit{\gamma }\end{array}\right]$$

The antisymmetric tensor of δΩ can be denoted as

$${\mathrm{\Delta }}_{\mathbf{R}}=\left[\begin{array}{ccc}\mathrm{0}& -\mathit{\delta }{\mathbf{\Omega }}_z& \mathit{\delta }{\mathbf{\Omega }}_y\\ \mathit{\delta }{\mathbf{\Omega }}_z& \mathrm{0}& -\mathit{\delta }{\mathbf{\Omega }}_x\\ -\mathit{\delta }{\mathbf{\Omega }}_y& \mathit{\delta }{\mathbf{\Omega }}_x& \mathrm{0}\end{array}\right]$$

Therefore, the matrix δR in Eq. (2) can be written as

$$\begin{array}{rl}& \mathit{\delta }\mathbf{R}={\mathrm{\Delta }}_{\mathbf{R}}\mathbf{R}=\\ & \left[\begin{array}{c}\mathrm{0}\\ -\sin \mathit{\beta }\mathit{\delta }\mathit{\alpha }+\mathit{\delta }\mathit{\gamma }\\ -\cos \mathit{\gamma }\mathit{\delta }\mathit{\beta }-\sin \mathit{\gamma }\cos \mathit{\beta }\mathit{\delta }\mathit{\alpha }\end{array}\right.\\ & \begin{array}{c}\sin \mathit{\beta }\mathit{\delta }\mathit{\alpha }-\mathit{\delta }\mathit{\gamma }\\ \mathrm{0}\\ -\sin \mathit{\gamma }\mathit{\delta }\mathit{\beta }+\cos \mathit{\gamma }\cos \mathit{\beta }\mathit{\delta }\mathit{\alpha }\end{array}\\ & \left.\begin{array}{c}\cos \mathit{\gamma }\mathit{\delta }\mathit{\beta }+\sin \mathit{\gamma }\cos \mathit{\beta }\mathit{\delta }\mathit{\alpha }\\ \sin \mathit{\gamma }\mathit{\delta }\mathit{\beta }-\cos \mathit{\gamma }\cos \mathit{\beta }\mathit{\delta }\mathit{\alpha }\\ \mathrm{0}\end{array}\right]\mathbf{R}\end{array}$$

Since the nominal orientation angles α, β, and γ of the frame $\mathit{\left\{}{O}_{A^{\prime }}\mathit{\right\}}$ with respect to base frame {O_B} are all zeros in the geometric configuration of the SSMP and the L/R mechanism, δR can be simplified as

$$\begin{array}{}\text{(4)}& \mathit{\delta }\mathbf{R}={\mathrm{\Delta }}_{\mathbf{R}}\mathbf{R}=\left[\begin{array}{ccc}\mathrm{0}& -\mathit{\delta }\mathit{\gamma }& \mathit{\delta }\mathit{\beta }\\ \mathit{\delta }\mathit{\gamma }& \mathrm{0}& -\mathit{\delta }\mathit{\alpha }\\ -\mathit{\delta }\mathit{\beta }& \mathit{\delta }\mathit{\alpha }& \mathrm{0}\end{array}\right]\mathbf{R}\end{array}$$

where Δ_R is an antisymmetric tensor of δΩ; let ${\mathit{c}}_i=\mathbf{R}({\mathit{a}}_i+l_i{\mathit{u}}_i)$, Eq. (2) can be rewritten in a compact form as

$$\begin{array}{}\text{(5)}& \mathit{\delta }{\mathit{b}}_i=\left[\begin{array}{cc}E& {\mathrm{\Delta }}_{c_i}^T\end{array}\right]\left[\begin{array}{c}\mathit{\delta }\mathit{p}\\ \mathit{\delta }\mathbf{\Omega }\end{array}\right]+\mathbf{R}\cdot \left(\mathit{\delta }{\mathit{a}}_i+\mathit{\delta }{l}_i\cdot {\mathit{u}}_i+l_i\cdot {\mathrm{\Delta }}_{u_i}\cdot {\mathit{u}}_i\right)\end{array}$$

where E is a 3×3 unit matrix; ${\mathrm{\Delta }}_{c_i}$ is an antisymmetric tensor of vector c_i.

The nominal parameters in Eq. (5) can be determined as follows: the nominal orientation angles α, β, and γ of the backplane are set zeros, therefore the orientation matrix R becomes a 3×3 unit matrix; The unit vector u_i with nominal value $(\mathrm{0},\mathrm{0},-\mathrm{1}{)}^T$ for each lead screw synchronizes with frame $\mathit{\left\{}{O}_{A^{\prime }}\mathit{\right\}}$ while micro rotating of frame $\mathit{\left\{}{O}_{A^{\prime }}\mathit{\right\}}$ occurs. The x and y components of vector δu_i can be approximated with micro rotational angles, Δθ₁ and Δθ₂, for a lead screw about its own x and y axes, respectively, and z component of u_i is zero. Thus, Eq. (5) can be unfolded as follows

$$\begin{array}{}\text{(6)}& \begin{array}{rl}\left[\begin{array}{c}\mathit{\delta }{b}_{i,x}\\ \mathit{\delta }{b}_{i,y}\\ \mathit{\delta }{b}_{i,z}\end{array}\right]=& \left[\begin{array}{cccccc}\mathrm{1}& \mathrm{0}& \mathrm{0}& \mathrm{0}& a_{i,z}-l_i& -a_{i,y}\\ \mathrm{0}& \mathrm{1}& \mathrm{0}& l_i-a_{i,z}& \mathrm{0}& a_{i,x}\\ \mathrm{0}& \mathrm{0}& \mathrm{1}& a_{i,y}& -a_{i,x}& \mathrm{0}\end{array}\right]\\ & \left[\begin{array}{c}\mathit{\delta }{x}_p\\ \mathit{\delta }{\mathrm{y}}_p\\ \mathit{\delta }{z}_p\\ \mathit{\delta }\mathit{\alpha }\\ \mathit{\delta }\mathit{\beta }\\ \mathit{\delta }\mathit{\gamma }\end{array}\right]+\left[\begin{array}{c}\mathit{\delta }{a}_{i,x}\\ \mathit{\delta }{a}_{i,y}\\ \mathit{\delta }{a}_{i,z}\end{array}\right]+\left[\begin{array}{c}\mathrm{0}\\ \mathrm{0}\\ -\mathit{\delta }{l}_i\end{array}\right]\\ +& l_i\left[\begin{array}{ccc}\mathrm{0}& -\mathit{\delta }{u}_{i,z}& \mathit{\delta }{u}_{i,y}\\ \mathit{\delta }{u}_{i,z}& \mathrm{0}& -\mathit{\delta }{u}_{i,x}\\ -\mathit{\delta }{u}_{i,y}& \mathit{\delta }{u}_{i,x}& \mathrm{0}\end{array}\right]\left[\begin{array}{c}\mathrm{0}\\ \mathrm{0}\\ -\mathrm{1}\end{array}\right]\end{array}\end{array}$$

where δl_i refers to the axial error Δl_i of the ith lead screw which is contributed by the gear train in the L/R mechanism, and is irrelevant with other geometrical errors investigated above.

Table 1 Nominal parameters for the L/R mechanism.

Table 2 Geometric errors of the L/R mechanism.

3.2 Halton-set based MC simulation

The technique of MC simulation has been received continual recognition in engineering practice. As one of the diagnostic process in tolerance design, MC simulation provides the statistics of output errors that assist the designer to make reasonable tolerance design of a product. However, there are two main problems for MC techniques: (a) time consumption for a large scale problem is unaffordable; and (b) solution precision for a median problem is unacceptable. Therefore, improving the precision and efficiency for a MC simulation is essential.

In recent decades, the NTM gradually became popular in computational mathematics area, and prevailed over traditional MC techniques in precision and efficiency. Instead of pseudo-random set in statistical simulation, the NTM applies LDS, whose points scatter evenly in a unit cubic, and whose regularity can be evaluated mathematically. The NTM based simulation could provide a higher convergence rate induced by its computation complexity of $O({\log }_N^s/N)$ than that induced by the one of $O\left(N^{-\mathrm{1}/\mathrm{2}}\right)$ provided by pseudo-random based MC simulation, where s represents the dimension of the investigated problem.

For Halton sequence (Halton, 1960), each point k can be represented by a m-ary expansion:

$$\begin{array}{}\text{(7)}& k=b_{\mathrm{0}}+b_{\mathrm{1}}m+b_{\mathrm{2}}{m}^{\mathrm{2}}+\mathrm{\dots }+b_r{m}^r\end{array}$$

where m is a prime number less than integer $b_i,\mathrm{0}<b_i<m-\mathrm{1}$, $i=\mathrm{0},\mathrm{1},\mathrm{2}\mathrm{\dots }r$. The component of each point in Halton-set can be represented by a radical inverse function y_m(⋅) defined as

$$\begin{array}{}\text{(8)}& y_m\left(k\right)=b_{\mathrm{0}}{m}^{-\mathrm{1}}+b_{\mathrm{1}}{m}^{-\mathrm{2}}+\mathrm{\dots }+b_r{m}^{-r-\mathrm{1}}\end{array}$$

where $y_m\left(k\right)\in (\mathrm{0},\mathrm{1})$, and the each point, X_k, in Halton-set with s-dimension, can be expressed as

$$\begin{array}{}\text{(9)}& X_k=\left[y_{m_{\mathrm{1}}}\left(k\right),y_{m_{\mathrm{2}}}\left(k\right),\mathrm{\dots },y_{m_s}\left(k\right)\right]\end{array}$$

where a set of pairwise coprime m₁, $m_{\mathrm{2}},\mathrm{\dots },m_s$ are selected as dimensional bases. Generally, the first s prime numbers are favorable in simulation.

3.3 Effectiveness comparison

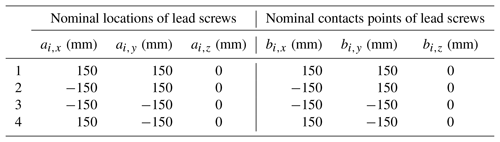
A comparison to output errors of the L/R mechanism for traditional (pseudo-random based) and Halton-set based MC simulation, are performed. All the parameters for the L/R mechanism are listed in Table 1. All the geometric errors in Eq. (6) are presumed to conform to uniform distribution within their tolerance zone, and listed in Table 2. The simulation comparison employs the sample size of 0.5×10³, 2.0×10³, 4.0×10³, 6.0×10³, 8.0×10³, 1.0×10⁴, and 1.2×10⁵. Standard deviations of output errors are represented by the x, y and z error of the end of each lead screw and listed in Table 3. Variations of standard deviation convergences are shown in Fig. 5.

The relative error σ_R is selected to evaluate the precision between two approaches and defined as

$$\begin{array}{}\text{(10)}& {\mathit{\sigma }}_R={\displaystyle \frac{\left|{\mathit{\sigma }}_{\text{S}}-{\mathit{\sigma }}_{\text{T}}\right|}{{\mathit{\sigma }}_{\text{T}}}}\times \mathrm{100}\mathit{\%}\end{array}$$

where σ_S represents standard deviation simulated with either approach, and σ_T is theoretical standard deviation with analytic error model in Eq. (6).

Table 3 Standard deviations σ of the L/R mechanism output error with pseudo-random and Halton-set based MC simulation.

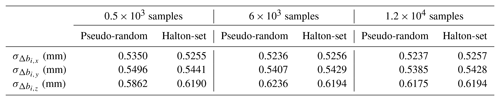
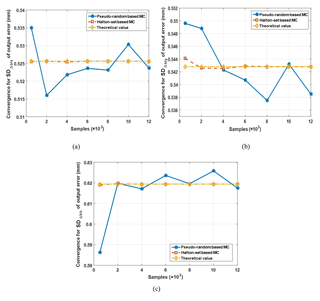
Figure 5 Convergence contrasts with pseudo-random and Halton-set based MC simulation for standard deviation of output errors for the L/R mechanism.

Figure 5 illustrates that the standard deviation ${\mathit{\sigma }}_{\mathrm{\Delta }{b}_{i,x}}$, ${\mathit{\sigma }}_{\mathrm{\Delta }{b}_{i,y}}$, or ${\mathit{\sigma }}_{\mathrm{\Delta }{b}_{i,z}}$ of the L/R mechanism' output errors with Halton-set based MC simulation, has a higher convergence rate than those with pseudo-random based one. The theoretical values of the statistics ${\mathit{\sigma }}_{\mathrm{\Delta }{b}_{i,x}}$, ${\mathit{\sigma }}_{\mathrm{\Delta }{b}_{i,y}}$, or ${\mathit{\sigma }}_{\mathrm{\Delta }{b}_{i,z}}$, are processed with the L/R mechanism error model in Eq. (6), and based on the nominal parameters in Table 1 and parameters' errors in Table 2. To reach the same simulation precision, for instance, we simply define a relative error of σ_R≤0.1 %. For ${\mathit{\sigma }}_{\mathrm{\Delta }{b}_{i,x}}$, it is achieved with a sample size of 500 by Halton-set. It is smaller than that of 1.2×10⁵ by pseudo-random based MC simulation; for ${\mathit{\sigma }}_{\mathrm{\Delta }{b}_{i,y}}$, it is achieved with a sample size of 2×10³ by Halton-set, and it is smaller than that of 4×10³ by pseudo-random based MC simulation; for ${\mathit{\sigma }}_{\mathrm{\Delta }{b}_{i,z}}$, it is achieved with a sample size of 500 by Halton-set, and it is also smaller than that of 2×10³ by pseudo-random based MC simulation. Additionally, the convergences for ${\mathit{\sigma }}_{\mathrm{\Delta }{b}_{i,y}}$ and ${\mathit{\sigma }}_{\mathrm{\Delta }{b}_{i,z}}$ with pseudo-random based MC simulation fluctuate significantly. In the following section, the tolerance synthesis process is therefore performed with Halton-set based MC simulation for responses of DOE.

We have found that as the dimension of a problem increases, the priorities in analytical precision and efficiency based on NTM are more significant over traditional Monte Carlo simulation. This simulation belongs to a 12-dimension problem, and Li et al had applied Sobol-set based MC in tackling accuracy analysis problem of a six-dof docking mechanism with 42 dimensions (Li et al., 2015). as the dimension increases, the pseudo-random cannot guaranty the investigated space where the high-dimension points uniformly are scatted. Additionally, there are some differences in the construction methods of different point sets. With the deepening of the number theory research, point set construction methods to improve the accuracy and efficiency of analysis will continue to emerge.

4 Tolerance synthesis

Taguchi (Rout and Mittal, 2006, 2007, 2008) suggests that the quality of a product is not ensured in the checking stage, but determined in the design stage. A reasonable tolerance assignment could not only facilitate production process but also bring about better performance of a product.

Generally, traditional tolerance synthesis for a mechanism is considered as a typical optimization technique. It aims at achieving a compromise between tolerance and cost, under constraints of various quality criterions. The optimized tolerance is then directly applied in the mechanism manufacturing, without much modification. This is currently a general process for mechanism development in a laboratory.

However, in contemporary manufacturing enterprise, there are plenty of stochastic factors disturbing process capacity dynamically; traditional synthesis approach is not perfectly suitable to modern production. It is necessary to propose an enterprise oriented mechanism's tolerance synthesis approach, which generates tolerance assignments with enough flexibility to adapt to stochastic variations of capacity.

4.1 DOE based synthesis methodology

In view of DOE, different tolerance as factors in a mechanism can be considered as independent dimensions. They are spanning a multi-dimensioned space, which can be regarded as “tolerance space”. In this space, the boundaries can be estimated by manufacturing capability, potentially feasible tolerance assignments are enveloped.

In tolerance space, different tolerance has their corresponding sensitivities to mechanism output performance. Tolerance sensitivity can be provided through range analysis. Then we can use their sensitivities to update levels of different tolerance, as level variation of any tolerance contributes equivalent influence on the mechanism output performance.

With the newly updated levels, how they can be merged into expected tolerance assignments, is an interesting and practical problem. An intuitive idea is to enumerate all the levels of all the factors, however, as the number of tolerance factor or levels increases, the sorting process may possibly result in a combinational explosion.

A compromise approach is to select representative combinations of levels in tolerance space. The representative combinations, as tolerance assignments, can be determined by a uniform DOE array, with good uniformity and neat comparability. They can optimally cover the tolerance space and be tolerant to capacity variation well.

The uniform DOE, short for uniform design, is proposed in the 1980s by Fang and Wang (1994), and is distinct from typical orthogonal design and Latin square design. The uniform experiment points are uniformly scattered within the whole experiment space, and fewest representative experiment points can disclose most information of a system, other than the rest types of DOE.

Uniform DOE (Fang and Lin, 2007) is particularly proficient in tackling high dimensional problem with factors and levels of large numbers. Uniformity of a uniform DOE can be measured through L₂-discrepency as follows:

Given a s-dimensioned super-cube C${}^s=[\mathrm{0},\mathrm{1}{]}^s$, a set of experiment points $P=\mathit{\{}{x}_{\mathrm{1}},\mathrm{\dots },x_n\mathit{\}}$ is constructed and distributed within the entire experiment space as uniformly as possible. L₂-discrepency, short for CD₂(⋅), is used to evaluate the uniformity of the point set P and can be written as follows

$$\begin{array}{}\text{(11)}& {\displaystyle }\begin{array}{rl}& {\left({\text{CD}}_{\mathrm{2}}\left(P\right)\right)}^{\mathrm{2}}=\\ & {\left({\displaystyle \frac{\mathrm{13}}{\mathrm{12}}}\right)}^s-{\displaystyle \frac{\mathrm{2}}{n}}\sum _{k=\mathrm{1}}^n\prod _{j=\mathrm{1}}^s\left(\mathrm{1}+{\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}\left|x_{k,j}-\mathrm{0.5}\right|-{\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}{\left|x_{k,j}-\mathrm{0.5}\right|}^{\mathrm{2}}\right)\\ & +{\displaystyle \frac{\mathrm{2}}{n}}\sum _{k=\mathrm{1}}^n\sum _{j=\mathrm{1}}^n\prod _{i=\mathrm{1}}^s\left(\mathrm{1}+{\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}\left|x_{k,j}-\mathrm{0.5}\right|\right.\\ & \left.+{\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}\left|x_{j,i}-\mathrm{0.5}\right|-{\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}\left|x_{k,j}-x_{j,i}\right|\right)\end{array}\end{array}$$

where $x_k=(x_{k,\mathrm{1}},\mathrm{\dots },x_{k,s})$ is the kth experiment point. In terms of the point set generation rule, the experiment space is consistently filled with uniform points of different quantity, therefore, the set of tolerance assignments, as experiment points, can be ultimately formulated. With a proper uniform design array, a tolerance assignment set can also be available.

4.2 DOE based synthesis procedure

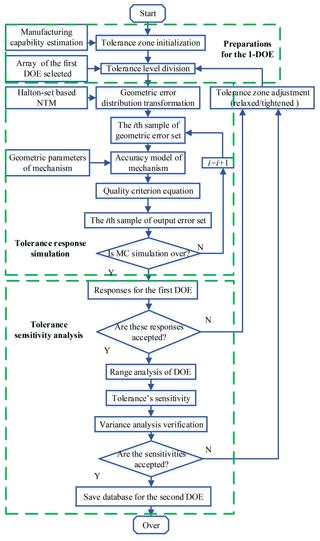
In the first stage of DOE, a proper DOE array is firstly selected in terms of the tolerance factor. Tolerance levels are initially evenly divided with geometric tolerance determined by manufacturing capacity, since we do not have any knowledge of their sensitivity. Then Halton-set based MC simulation is employed for DOE response, please refer to Sect. 3.2. Through range and variation analysis techniques, the sensitivities of geometric tolerances are subsequently obtained. Figure 6 detailed the scheme of the first stage of DOE for factor sensitivities, which mainly includes preparations for 1-DOE, tolerance response simulation and tolerance sensitivity analysis.

The second stage of DOE aims at generating uniformly distributed tolerance assignments. Sensitive factors are set with the highest level, the rest insensitive ones are re-divided into levels, whose intervals are inversely proportional to their sensitivities, and therefore levels of tolerance factors can produce an equivalent impact on response. In this stage, DOE responses are also generated by Halton-set based MC simulation, please refer to Sect. 3.2.

4.3 Definition and Strategy

DOE based tolerance synthesis for a mechanism has to: define response function, arrange tolerance factors and levels, and devise other detail strategies related to tolerance assignment. They are addressed as follows.

Figure 6 Scheme for the first stage of DOE for the L/R mechanism's tolerance synthesis.

4.3.1 Response function definition

The tolerance stack-up is used to reflect the success rate of the assembled mechanism, and evaluate manufacturing quality whether this tolerance assignment is acceptable. It involves two aspects: radical error Δr_i of each lead screw and non-synchronous error Δz of all 4 lead screws of the mechanism, they can be respectively defined as

$$\begin{array}{}\text{(12)}& {\displaystyle }\mathrm{\Delta }{r}_i=\sqrt{\mathrm{\Delta }{x}_{p,i}^{\mathrm{2}}+\mathrm{\Delta }{y}_{p,i}^{\mathrm{2}}}\le \mathrm{\Delta }{r}_{\mathrm{0}}\text{(13)}& {\displaystyle }\begin{array}{rl}\mathrm{\Delta }z& =max(\mathrm{\Delta }{z}_{p,i}-\mathrm{\Delta }{z}_{p,j})\le \mathrm{\Delta }{z}_{\mathrm{0}}\\ & (i,j=\mathrm{1},\mathrm{2},\mathrm{3}\text{or}\mathrm{4})(i\ne j)\end{array}\end{array}$$

where Δx_p,i and Δy_p,i denote the end errors of a lead screw along x and y axis respectively, and can be obtained from Eq. (6). Δr₀ represents the allowed threshold of a radical error in a side surface of SSMP in Fig. 4. Δz₀ is the permitted threshold of non-synchronous error.

It is noted that there is a statistical process. We define an event “M_i” as an occurrence of the radical error Δr_i of the ith screw's end, within the threshold of Δr₀, which can be expressed as Δr_i<Δr₀. Then another event “N” is defined as an occurrence of non-synchronous error along z axis among the ends of screws, within a threshold of Δz₀, which can be expressed as “Δz<Δz₀”. The tolerance stack-up is the probability of all the events “M_i” (i=1, 2, 3, or 4) and “N”, occurring at the same time. Thus, the tolerance stack-up can be expressed as a probability of multi-event production, since they are independent with each other:

$$\begin{array}{}\text{(14)}& {\displaystyle }\begin{array}{rl}\mathit{P}\left(M_{\mathrm{1}}{M}_{\mathrm{2}}{M}_{\mathrm{3}}{M}_{\mathrm{4}}N\right)& =\mathit{P}\left(N\right|M_{\mathrm{1}}{M}_{\mathrm{2}}{M}_{\mathrm{3}}{M}_{\mathrm{4}}N)\\ & \times \mathit{P}\left(M_{\mathrm{1}}\right|M_{\mathrm{2}}{M}_{\mathrm{3}}{M}_{\mathrm{4}})\times \mathit{P}(M_{\mathrm{2}}\left|M_{\mathrm{3}}{M}_{\mathrm{4}}\right)\\ & \times \mathit{P}\left(M_{\mathrm{3}}\right|M_{\mathrm{4}})\times \mathit{P}(M_{\mathrm{4}})\end{array}\end{array}$$

We can take 99.73 % as a threshold of the tolerance stack-up, in terms of “6σ” principle in production quality control theory. It means if a combination of tolerance levels in the uniform DOE yields a response P(M₁M₂M₃M₄N)>99.73 %. This combination can be accepted as one of potentially feasible candidate tolerance assignment. A detailed schematic for simulation process is outlined in Fig. 7.

4.3.2 Arrangements for factors and levels

In a tolerance synthesis, geometric tolerance of a mechanism as factors are considered before a proper DOE array is determined. The first stage of DOE is designed to obtain a general knowledge of sensitivity of different tolerance factor. Therefore, over-condensed levels are not necessary for DOE analytical efficiency.

4.3.3 Strategy for level re-division

For the second DOE stage, interval between adjacent levels of a tolerance factor follows inverse proportion to its own sensitivity, as to place an equivalent impact on mechanism output performance. The level re-division follows three steps:

• a.

  Identifying the most insensitive factor, and conserving its sensitivity as R; the interval Δ_i between adjacent levels of the rest factors is expressed as:

  $$\begin{array}{}\text{(15)}& {\mathrm{\Delta }}_i={\displaystyle \frac{R_i}{R}}\times {\displaystyle \frac{{\text{Th}}_i-{\text{Tl}}_i}{n}}\end{array}$$

  where R_i denotes the sensitivity of the ith tolerance factor; Th_i and Tl_i denote the upper and lower bounds of the ith tolerance factor, respectively, n denotes the expected number of levels.

• b.

  Determining new levels of all factors as:

  $$\begin{array}{}\text{(16)}& L_{i,j}={\text{Tl}}_i+{\mathrm{\Delta }}_i\times (j-\mathrm{1})\left(\mathrm{0}<j<\left({\displaystyle \frac{{\text{Th}}_i-{\text{Tl}}_i}{{\mathrm{\Delta }}_i}}\right)\right)\end{array}$$

  where L_i,j refers to the jth level of the ith factor, and j is an integral number.

• c.

  Simulating with Halton-set based MC approach with these newly updated levels, and yielding tolerance stack-ups as responses.

Figure 7 Scheme of Halton-set based simulation for the tolerance stack-up and for each column in the uniform DOE array.

4.4 Illustrative example

The L/R mechanism discussed is shown in Fig. 4, the whole tolerance synthesis is presented as follows:

4.4.1 Parameters initialization

Quality index requirement

The radical error Δr₀ defined in Eq. (12) is set with 1.6 mm, which means radical deviations for all the screw ends are restricted within 1.6 mm. The non-synchronous error Δz₀ defined in Eq. (13) is configured with 1.6 mm. To ensure the manufacturing quality, the tolerance stack-up should be no less than 99.73 % in terms of “6σ” principle.

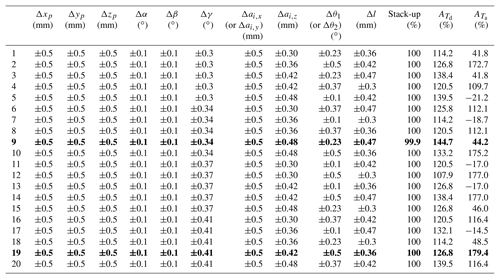
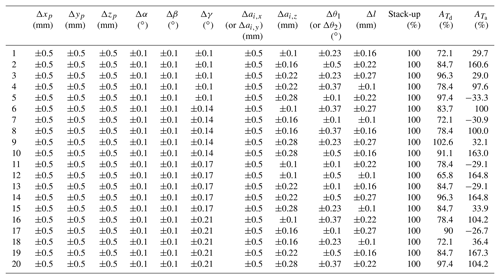
Traditional tolerance synthesis approach comes from experience in practice, does not place sufficient concern on the sensitivity of different tolerance. That makes the tolerance assignment become less flexible, and limits the assembly application. In terms of experience, the tolerance assignment is obtained and listed in Table 4, and whose stack-up is processed with the scheme described in Fig. 7, and finally reaches up to 99.99 % (> 99.73 % of “6σ”). This tolerance assignment is acceptable for a successful assembly of the L/R mechanism, however, as manufacturing capacity varies, its feasibility is still doubtful.

Table 4 Experience based tolerance assignment for the L/R mechanism.

Table 5 Levels division of L₂₇(3¹⁰) array for geometric tolerance factors.

Table 6 L₂₇(3¹⁰) orthogonal array for responses with a sample size of 10⁵ using Halton-set based MC simulation.

Figure 8 Convergence of the sensitivities for 10 tolerance factors.

Tolerance factors' initialization

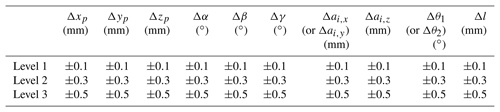
All the geometric tolerance factors are initialized as follows: the permitted limitations of dimensional tolerances involving Δx_p, Δy_p, Δz_p, Δa_i,x, Δa_i,y, Δa_i,z, Δl are no less than ±0.1 mm; and permitted those of angular tolerances involving Δα, Δβ, Δγ, Δθ₁, Δθ₂ are no less than ±0.1^∘. Since the technological process tolerance Δa_i,x for a lead screw, resembles that of Δa_i,y, they are regarded as the same factor; similarly, the same analysis is for Δθ₁ and Δθ₂ which can also be regarded as the same factor. Therefore, 10 tolerance factors are finally determined: Δx_p, Δy_p, Δz_p, Δα, Δβ, Δγ, Δa_i,x (or Δa_i,y), Δa_i,z, Δθ₁ (or Δθ₂) and Δl.

Table 7 Variance analysis for the sensitivities of the tolerance factors.

^* Significant at 0.025 % ($F_{\mathrm{0.025}}(\mathrm{2},\mathrm{12})=\mathrm{5.1}$).

4.4.2 The first stage of DOE

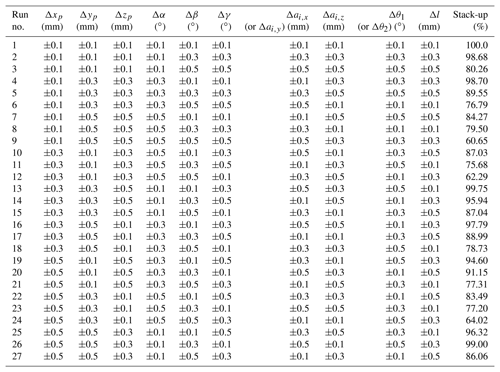
With DOE based tolerance synthesis discussed above, the orthogonal array L₂₇(3¹⁰) is chosen for the first stage of DOE. It accommodates 10 factors, three levels for per factor and 27 combinations, can be considered as an appropriate arrangement for compromise between efficient and precise simulation, and is listed in Table 5.

With the first DOE in Table 5, the responses are obtained through a sample size of 10⁵ Halton-set based MC simulation and tabulated in Table 6.

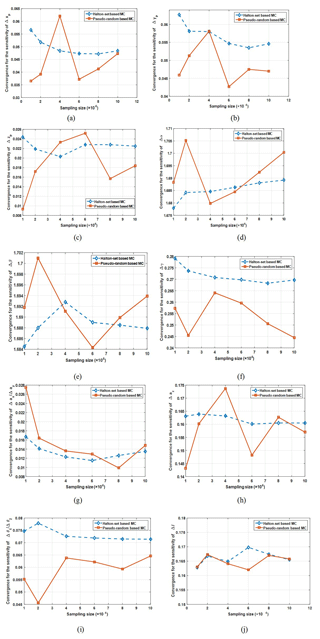
For precise tolerance sensitivity in the first stage, a convergence comparison with pseudo-random and Halton-set based MC simulation is conducted according to the schemes shown in Figs. 6 and 7. Sample sizes are 1×10⁴, 2×10⁴, 4×10⁴, 6×10⁴, 8×10⁴ and 1×10⁵. The convergences of sensitivities for 10 tolerance factors are plotted in Fig. 8.

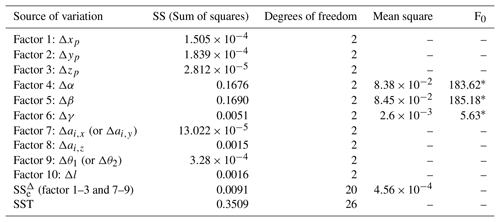
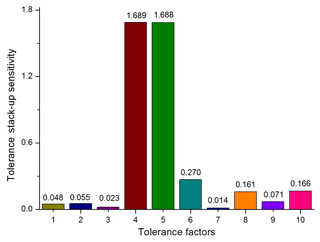
From the convergence of sensitivities for 10 tolerance factors, obtained in Fig. 8, we can be found that the tolerance sensitivities convergence with Halton-set based MC simulation, generally maintains a steadier process than that with pseudo-random based one. By comparison, these statistics with Halton-set based NTM simulation is more reliable than that with pseudo-random in convergence precision. The final tolerance sensitivities, with a sample size of 10⁵ Halton-set based MC simulation is depicted in Fig. 9. The analysis of variance is then carried out, to verify the tolerance sensitivities as listed in Table 7.

Tolerance factor sensitivities have been yielded through range analysis in Fig. 9. Variance analysis in Table 7 confirms that the orientation angular errors, Δα and Δβ, for backplane of the L/R mechanism are the most sensitive factors, and they should be tightly controlled during the manufacturing process. Therefore, in the second stage of DOE for tolerance assignment, the sensitive factors, Δα and Δβ, are configured with top levels ±0.1^∘ of permitted tolerances; the insensitive ones such as Δx_p, Δy_p, Δz_p, and Δa_i,x (or Δa_i,y), can be assigned with a more relaxed tolerance ±0.5 mm; and the rest ones including Δγ, Δa_i,z, Δθ₁ (or Δθ₂) and Δl with their permitted tolerance zones, are put into the second stage of the uniform DOE for final tolerance assignment.

Figure 9 Tolerance stack-up sensitivities for the tolerance factors.

4.4.3 The Second stage of DOE

As discussed in Sect. 4.2, the more/less sensitive a factor is, the narrower/broader an interval of adjacent levels should be in general. Therefore, the interval for levels is expected to be inversely proportional to their sensitivities. The uniform array of U₂₀(4⁴) is properly enough by accommodating to 4 factors, 4 levels per factor and 20 combinations of levels. The combinations of different levels among factors with distributional regularity and uniformity, have an optimum coverage of the tolerance space, and avoid enumeration that may possibly result in a combination explosion. The levels re-divided for factors Δγ, Δa_i,z, Δθ₁ (or Δθ₂) and Δl are contained in Tables 8 and 9.

Table 8 Tolerance factor levels re-division for U₂₀(4⁴) array within tolerance zones (part A).

Table 9 Tolerance factor levels re-division for U₂₀(4⁴) array within tolerance zones (part B).

4.4.4 Tolerance assignment and evaluation

The newly updated levels of tolerance factors Δγ, Δa_i,z, Δθ₁ (or Δθ₂) and Δl, in Tables 8 and 9, are put into the uniform array U₂₀(4⁴). With the sensitive factors Δα and Δβ, and insensitive ones Δx_p, Δy_p, Δz_p, and Δa_i,x (or Δa_i,y), the candidate tolerance assignments are formulated. Consequently, the stack-ups as their responses, with a sample size of 10⁵ Halton-set based MC simulation, are produced in Tables 10 and 11.

Generally, the complexity of product manufacturing can be lowered down, as the tolerance is properly amplified. There may still be reachable compromise between reliability and economy in tolerance assignments. We usually define different functions to evaluate manufacturing consumption. Typical cost-tolerance functions, such as linear, exponential, inverse square, and power series one (Singh, 2009a, b), could precisely express the relations between tolerance and consumption. When applied in a particularly compound process, these types of cost-tolerance functions need to be modified with experience.

Compared to tolerance determined by experience in tolerance relaxation, we simply choose the linear accumulative tolerance as cost-tolerance function, to make comparison of tolerance relaxation. Thus, the cost-tolerance dimensional and angular functions, $T_{{\sum }_{\text{d}}}$ and $T_{{\sum }_{\text{a}}}$, can be defined as

$$\begin{array}{}\text{(17)}& {\displaystyle }\begin{array}{rl}{T}_{{\mathrm{\Sigma }}_{\text{d}}}& =\mathrm{\Delta }{x}_p+\mathrm{\Delta }{y}_p+\mathrm{\Delta }{z}_p\\ & +\mathrm{4}(\mathrm{\Delta }{a}_{i,x}+\mathrm{\Delta }{a}_{i,y}+\mathrm{\Delta }{a}_{i,z})+\mathrm{4}\mathrm{\Delta }l\\ T_{{\mathrm{\Sigma }}_{\text{a}}}& =\mathrm{\Delta }\mathit{\alpha }+\mathrm{\Delta }\mathit{\beta }+\mathrm{\Delta }\mathit{\gamma }+\mathrm{4}(\mathrm{\Delta }{\mathit{\theta }}_{\mathrm{1}}+\mathrm{\Delta }{\mathit{\theta }}_{\mathrm{2}})\end{array}\end{array}$$

Relaxation of dimensional and angular tolerance, $A_{T_{\text{d}}}$ and $A_{T_{\text{a}}}$, can be evaluated as

$$\begin{array}{}\text{(18)}& {\displaystyle }\begin{array}{rl}& A_{T_{\text{d}}}={\displaystyle \frac{T_{{\mathrm{\Sigma }}_{\text{2d}}}-T_{{\mathrm{\Sigma }}_{\text{1d}}}}{T_{{\mathrm{\Sigma }}_{\text{1d}}}}}\times \mathrm{100}\mathit{\%}\\ & A_{T_{\text{a}}}={\displaystyle \frac{T_{{\mathrm{\Sigma }}_{\text{2a}}}-T_{{\mathrm{\Sigma }}_{\text{1a}}}}{T_{{\mathrm{\Sigma }}_{\text{1a}}}}}\times \mathrm{100}\mathit{\%}\end{array}\end{array}$$

where $T_{{\sum }_{\text{1d}}}$ and $T_{{\sum }_{\text{1a}}}$ denote the dimensional and angular accumulated tolerance, respectively. They are originally determined by experience in terms of Table 4, with $T_{{\sum }_{\text{1d}}}=\mathrm{3.8}$ mm and $T_{{\sum }_{\text{1a}}}=\mathrm{1.65}$^∘. $T_{{\sum }_{\text{2d}}}$ and $T_{{\sum }_{\text{2a}}}$ of each assignment in rows in Tables 10 and 11 are processed with Eq. (14), and their relaxation ($A_{T_{\text{d}}}$ and $A_{T_{\text{a}}}$) are finally tabulated.

Table 10 Array U₂₀(4⁴) for responses with a sample size of 10⁵ using Halton-set based MC simulation (part A).

Table 11 Array U₂₀(4⁴) for responses with a sample size of 10⁵ using Halton-set based MC simulation (part B). The solutions with the maximums of $A_{T_{\text{d}}}$ and $A_{T_{\text{a}}}$ are denoted in bold front.

4.5 Discussion

Tolerance assignments in Tables 10 and 11 in series with uniform DOE, provide potentially feasible candidates with the application for the L/R mechanism manufacturing. All the stack-ups of assignments as response, are upper than 99.73 % in terms of “6σ” principle. It indicates that all of them satisfy manufacturing quality criteria. However, this does not mean all the initial tolerance bounds restricted by capacity, can definitely generate satisfying stack ups, since there may still be a few assignments unfeasible, however, it will not disable tolerance synthesis.

The relaxation, $A_{T_{\text{d}}}$ and $A_{T_{\text{a}}}$, of the tolerance assignments with positive signs, indicate the tolerance of the assignment is relaxed, compared to that of experience based tolerance assignment. Those with negative sign, indicate assignments a contractive tolerance. However, the majority of the mechanism's tolerances are significantly relaxed considering: $A_{T_{\text{d}}}$ is up to 144.7 % of the combination 9 in Table 11, and $A_{T_{\text{a}}}$ is up to 179.4 % of the combination 19 in Table 11; even though there are seven combinations with negative relaxation of $A_{T_{\text{a}}}$. Tolerance assignments with positive amplifications of $A_{T_{\text{d}}}$ and $A_{T_{\text{a}}}$ as candidates can facilitate the manufacturing process of the L/R mechanism.

In this research, the uniform DOE array used for tolerance assignments generation (other than the other ones) presents a fact that the combinations of the experiment have a uniform coverage of tolerance space. The uniformity and representativeness can be proved mathematically. Both the Halton-set based MC simulation for tolerance analysis, and uniform design used in accuracy synthesis of the L/R mechanism, are applicable extensions of LDS in NTM. The evenly scatted high-dimensional sampling points from NTM, have promoted the accuracy analytical precision and efficiency. It demonstrates NTM based MC approach prevails over traditional pseudo-random based one. While the uniform DOE array, provides more representative tolerance assignments, which can be in resistant to any tolerance applicative failure induced by manufacturing system's capacity disturbance.

5 Conclusions

This research proposed DOE based tolerance synthesis approach for mechanism tolerance synthesis, and applied for L/R mechanism with the application of the SSMP. Conclusions are drawn as follows:

• a.

  A Halton-set based MC simulation is introduced and utilized in tolerance synthesis process. Comparative results indicate that it could provide more efficient and precise convergence in tolerance analysis.

• b.

  A DOE based tolerance synthesis is proposed. Sensitivities of all the tolerance factors are revealed. Among them, the orientation angular errors Δα and Δβ, of the backplane of the L/R mechanism, are identified as the most significant factors, and validated through variance analysis.

• c.

  Tolerance assignments, with a uniform coverage of tolerance space, through uniform DOE are finally generated. The majority of assignments comply with the manufacturing criteria of 99.73 %, and they have different tolerance relaxation, compared to experience based tolerance assignment.

In the future research, tolerance synthesis will be extended to carry out investigations on structural parameters, material selections and dynamic response.

Appendix A: Variables and abbreviations

ai	Nominal position of the ith lead screw in the frame $\mathit{\left\{}{O}_{A^{\prime }}\mathit{\right\}}$
$A_{T_{\text{a}}}$	Amplification percentage of the angular tolerances
$A_{T_{\text{d}}}$	Amplification percentage of the dimensional tolerances
bi	Nominal vector of an ideal contact between the ith slot on SSMP and the end of
	the ith lead screw in base frame {OB}
ci	An vector of R(ai+liui)
CD2(⋅)	Criteria for the uniformity of a point set
DOE	Design of experiment
E	a 3×3 unit matrix
li	Nominal axial vector of ith lead screw
Li,j	The jth level of the ith factor
L/R	lock-or-release
LDS	Low discrepancy sequence
MC	Monte Carlo
NTM	Number-theory method
$\mathit{\left\{}{O}_{A^{\prime }}\mathit{\right\}}$	Frame attached on surface of backplane
{OB}	Frame attached on side surface of SSMP
p	Nominal displacement of frame $\mathit{\left\{}{O}_{A^{\prime }}\mathit{\right\}}$ with respect to base frame {OB}
R	Rotational matrix of frame $\mathit{\left\{}{O}_{A^{\prime }}\mathit{\right\}}$ with respect to base frame {OB}
R	the sensitivity of the least sensitive factor
Ri	The sensitivity of the ith factor
SSMP	Space Station Microgravity Platform
Thi	The upper bound of the ith tolerance factor
Tli	The lower bound of the ith tolerance factor
$T_{{\sum }_a}$	Angular tolerance accumulated
$T_{{\sum }_d}$	Dimensional tolerance accumulated
ui	unit vector (ux, uy, uz)T of the ith lead screw
δui	deviation of ui
Δai	Position error (Δai,x, Δai,y, Δai,z) of the ith lead screw fixed on the backplane
${\mathrm{\Delta }}_{c_i}$	Antisymmetric tensor of vector ci
Δi	The level interval of the ith factor
Δl	Axial error of a lead screw induced by total transmission error of transmission chain
ΔR	Antisymmetric tensor of δR
Δri	The radical error of the ith lead screw's end
Δr0	The threshold for the radical error Δri
Δz	The non-synchronous error along z axis among the ends of lead screws
Δz0	The threshold for the non-synchronous error Δz
ΔΩ	Angular error (Δα, Δβ, Δγ)T of a backplane about x, y and z axis of base frame {OB}
δbi	End error of theith lead screw in frame {OB}
δp	Displacement error (δxp, δyp, δzp)T of backplane
δxp	Locational error of a backplane along x axis of base frame {OB}
δyp	Locational error of a backplane along y axis of base frame {OB}
δzp	Locational error of a backplane along z axis of base frame {OB}
δα	Angular error of a backplane rotating around x axis of base frame {OB}
δβ	Angular error of a backplane rotating around y axis of base frame {OB}
δγ	Angular error of a backplane rotating around z axis of base frame {OB}
δR	Perturbation of rotational matrix R for frame $\mathit{\left\{}{O}_{A^{\prime }}\mathit{\right\}}$ to base frame {OB}
μ⋅	Mean of a statistic
σ(⋅)	The standard deviation operators in statistics
σR	Relative error between standard deviations obtained with both simulations
σS	Standard deviation simulated with either approach
σT	Theoretical standard deviation with analytic error model in Eq. (6)