Compound optimal control of harmonic drive considering hysteresis characteristic

Hysteresis behavior widely exists in the transmission process of harmonic drives. Eliminating the hysteresis effect is highly desired in the high-precision mechanical transmission, which results in challenges in the control design. This paper aims to improve the tracking accuracy of the motor-harmonic drive serial system. Firstly, a modified Bouc-Wen model based on uniform smooth approximating function is applied to describe the hysteresis behavior of the harmonic drive. By using coordinate transformation and accurate state feedback linearization, we then obtain the mathematical model of the serial system of the motor-harmonic drive. Finally, the reference trajectory is tracked by a compound optimal controller that is based on a linear quadratic regulator. Simulation results show that compared with the disturbance observer-based control (DOBC) using a linear observer, the new compound optimal controller in this paper presents a smoother control signal with the elimination of large amount of high-frequency oscillations. Furthermore, the relative error in the steady state tracking tends to approach to zero and no cyclic fluctuations appears. With the employing of optimal control, the output of the harmonic drive can trace more complex trajectory.

1 Introduction

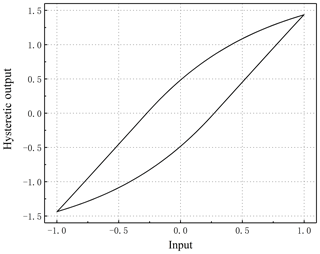
For an ideal transmission system, the phase diagram of the system state established by the input torque and output displacement should be a monotonic curve regardless of loading history. In other words, there should be a one-to-one correspondence between the output displacement and input torque of the system. In fact, hysteresis phenomena are widely recognized in the electromechanical transmission systems. Hysteresis generally means that the current state of the system depends not only on the input at the moment, but also depends on the history of input values, i.e. path-dependent processes (Mayergoyz et al., 2003; Bertotti et al., 1998), which results in lots of control difficulties.

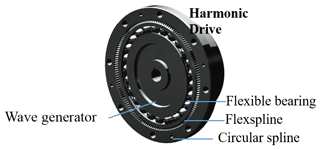
With the development of aerospace industries, as a new transmission system, the servo motor-harmonic drive serial system is widely used in transmission mechanisms of rockets and satellites. However, due to the nonlinear contact friction between the flexspline and the circular spline (as shown in Fig. 1), together with the viscous friction of the flexible bearing, transmission hysteresis characteristics exist in the servo motor-harmonic drive serial system. For example, for a basic transmission unit of a robot arm, these inherent nonlinear properties will result in serious hysteresis feature of the transmission system and adversely affect the motion precision of the robot arm. This paper focuses on the control of such a harmonic drive system with hysteresis characteristic.

Figure 1 Structures of harmonic drive.

Figure 2 shows a typical servo motor-harmonic drive serial system followed by an illustrative hysteresis loop as shown in Fig. 3. In engineering applications, there are different specific hysteresis behaviors for harmonic drives in which detailed experimental data are required to define. Kircanski et al. (1997) designed an experiment, in which two torque sensors were set up at both the input port of the motor and the output port of the harmonic drive, and the input torque curve of the motor was controlled to be a harmonic wave with a fixed maximum magnitude. It was found in the experiment that when the input torque returned to zero after several periods, the output of the harmonic drive was not zero. Dhaouadi et al. (2003) also conducted experimental testing to reveal the hysteresis, where the output port of the harmonic drive was locked and a periodic torque was forcibly exerted on the motor side. The experimental result showed that the hysteresis characteristic is insensitive to the input frequency when the input toque maintains a constant magnitude. The advantage of this experimental scheme lies in the ability of secure testing of the high-frequency input responses. Both the experimental results provide us with basis on the study of the hysteresis model so that we can select the corresponding parameters to establish an optimal control method with a higher precision for a hysteresis system.

Figure 2 Servo Motor-Harmonic Drive Serial System. θ_m is the rotation angle of the motor rotor, θ_l the rotation angle on the output port of the harmonic drive, and τ_m the output torque of servo motor.

Figure 3 Example of a Hysteresis Loop.

In literatures, there are many existing mathematical models proposed to describe hysteresis, such as LuGre model (Kamlah and Jiang, 1999), Preisach model (Song et al., 2005), Duhem model (Lee and Royston, 2000), Maxwell model (Huang and Chiu, 2009) and Bouc-Wen model (Zhu et al., 2014). Among these models, the Bouc-Wen model is a classical and most widely used one. However, this model is not differentiable everywhere, which will be improved in the present paper by using uniform smooth approximating function.

Meanwhile, there are also various control theories that can be used to compensate for hysteresis issues, including PID (proportional–integral–derivative) control, feed-forward controller, adaptive control, and sliding mode control.

PID controller does not depend on the specific structure of the controlled object, which makes it theoretically capable of solving the hysteresis problem. However, for the system with sharp changes, PID controller cannot compensate for the hysteresis torque in real time. Different from PID control, the feed-forward controller requires sophisticated modeling and precise parameters. Considering this, An et al. (1989) introduced the feed-forward control into a PD (proportional-derivative) control and used this compound method to control the robotic arm equipped with a harmonic drive.

Adaptive control is the most widely used method for hysteresis compensations. Many newly emerging control theories, such as fuzzy theory, internal model principle and neural network, have been utilized in combination with the adaptive control. For an unknown nonlinear friction model, Tadayoni et al. (2011) approximated the friction torque by using the wavelet network and fuzzy structure. However, implementing these compound controllers requires the control unit to provide certain challenging computing ability and data storage capacity. Under current technical conditions with ordinary industrial control chips, it is difficult to satisfy these requirements to implement such a compound control.

Sliding mode controller can compensate for the hysteresis in real time with high precision. Moreover, by using the sliding mode controller we can achieve the same control result at a relatively low cost. He et al. (2009) used a LuGre model as the controlled object of a sliding mode controller, with a successful simulation demonstration. Unfortunately, for the harmonic drive in engineering applications, the tremor caused by the high-frequency switching signals in the sliding mode controller can excite high-order unmodeled dynamics of the system. This consequence will seriously jeopardize the transmission precision of the system (Bandyopadhyay et al., 2015). In summary, these controllers are not suitable for a motor-harmonic drive electromechanical transmission system.

Considering the advances and the existing problems of these controllers, we will design a new controller based on the optimal control theory for the motor-harmonic drive system, with an objective of achieving the output tracking precision in an optimal status. In Sect. 2, we build a mathematical model of motor-harmonic drive system. This model considers the disturbance of the hysteresis torque which is compensated for by the precise state feedback linearization and a compound optimal controller. In Sect. 3, a new compound controller is proposed to improve the tracking accuracy of the motor-harmonic drive transmission system at the most extent. In Sects. 4 and 5, we validate the superiority of this new controller using numerical simulation, by comparing with the distribute observer based control (DOBC). Conclusions are drawn in Sec. 6.

2 Mathematical modeling of hysteresis characteristic of motor-harmonic drive system

The motor-harmonic drive system has two degrees of freedom, which are defined by the rotation angle of the motor rotor, θ_m, and the rotation angle on the output port of the harmonic drive, θ_l, as shown in Fig. 2. The Lagrange equations of the transmission system can be written as follows:

$$\begin{array}{}\text{(1)}& \left\{\begin{array}{l}{J}_{\text{m}}{\ddot{\mathit{\theta }}}_{\text{m}}+B_{\text{m}}{\dot{\mathit{\theta }}}_{\text{m}}+{\displaystyle \frac{K}{N}}\left({\displaystyle \frac{{\mathit{\theta }}_{\text{m}}}{N}}-{\mathit{\theta }}_{\text{l}}\right)+{\displaystyle \frac{\mathrm{1}}{N}}q={\mathit{\tau }}_{\text{m}},\\ J_{\text{l}}{\ddot{\mathit{\theta }}}_{\text{l}}+B_{\text{l}}{\dot{\mathit{\theta }}}_{\text{l}}-K\left({\displaystyle \frac{{\mathit{\theta }}_{\text{m}}}{N}}-{\mathit{\theta }}_{\text{l}}\right)-q=\mathrm{0},\\ \dot{q}+a\left|{\displaystyle \frac{{\dot{\mathit{\theta }}}_{\text{m}}}{N}}-\dot{{\mathit{\theta }}_{\text{l}}}\right|q-A\left({\displaystyle \frac{{\dot{\mathit{\theta }}}_{\text{m}}}{N}}-\dot{{\mathit{\theta }}_{\text{l}}}\right)=\mathrm{0},\end{array}\right.\end{array}$$

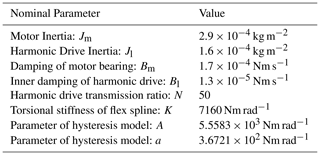
where J_m and J_l are the inertia moment of the moving part of the motor and the inertia moment of the loading end, respectively, K the torsional stiffness between the input and output ports of the harmonic drive, and N the transmission ratio.

With the third nonlinear differential formula in Eq. (1), one can obtain the hysteresis torque q. This formula is the special form of the standard Bouc-Wen model with particular parameters of n=1 and β=0 (Gandhi et al., 2001). The fitting results of experimental data fromIkhouane et al. (2007) indicate that the model with only two positive parameters, a and A, can already well describe the hysteresis in the harmonic drive. B_m and B_l in Eq. (1) represent viscous damping coefficients inside the motor and harmonic drive, respectively. The two parameters are acquired according to the experimental data.

If we define the state variable vector as $\mathit{x}=[x_{\mathrm{1}},x_{\mathrm{2}},x_{\mathrm{3}},x_{\mathrm{4}},x_{\mathrm{5}}{]}^T=[{\dot{\mathit{\theta }}}_{\text{m}},{\mathit{\theta }}_{\text{m}},{\dot{\mathit{\theta }}}_{\text{l}},{\mathit{\theta }}_{\text{l}},q{]}^T$, Eq. (1) can be rewritten into the form of state space as below:

$$\begin{array}{}\text{(2)}& \left\{\begin{array}{l}{\dot{x}}_{\mathrm{1}}=-{\displaystyle \frac{B_{\text{m}}}{J_{\text{m}}}}{x}_{\mathrm{1}}-{\displaystyle \frac{K}{J_{\text{m}}{N}^{\mathrm{2}}}}{x}_{\mathrm{2}}+{\displaystyle \frac{K}{J_{\text{m}}N}}{x}_{\mathrm{4}}-{\displaystyle \frac{\mathrm{1}}{J_{\text{m}}N}}{x}_{\mathrm{5}}+u,\\ {\dot{x}}_{\mathrm{2}}=x_{\mathrm{1}},\\ {\dot{x}}_{\mathrm{3}}={\displaystyle \frac{B_{\text{l}}}{J_{\text{l}}}}{x}_{\mathrm{3}}-{\displaystyle \frac{K}{J_{\text{l}}}}{x}_{\mathrm{4}}+{\displaystyle \frac{K}{J_{\text{l}}N}}{x}_{\mathrm{2}}+{\displaystyle \frac{\mathrm{1}}{J_{\text{l}}}}{x}_{\mathrm{5}},\\ {\dot{x}}_{\mathrm{4}}=x_{\mathrm{3}},\\ {\dot{x}}_{\mathrm{5}}=-a\left|{\displaystyle \frac{x_{\mathrm{1}}}{N}}-x_{\mathrm{3}}\right|x_{\mathrm{5}}+A\left({\displaystyle \frac{x_{\mathrm{1}}}{N}}-x_{\mathrm{3}}\right).\end{array}\right.\end{array}$$

The compact form of Eq. (2) is:

$$\begin{array}{}\text{(3)}& \left\{\begin{array}{l}\dot{x}=f\left(\mathit{x}\right)+g\left(\mathit{x}\right)u,\\ y=h\left(\mathit{x}\right)=\left[\mathrm{0},\mathrm{0},\mathrm{0},\mathrm{1},\mathrm{0}\right]\mathit{x}.\end{array}\right.\end{array}$$

The system described by Eq. (3) is a typical nonlinear affine single-input single-output (SISO) system (Dierks et al., 2010), in which the system input is the motor torque u and the output is the angular displacement θ_l of the output port of the harmonic drive. The absolute value function in Eq. (3) keeps us from calculating the analytic solution of its Jacobian matrix. So in the present paper, uniformly smooth approximating functions are used to approximate the absolute value function (for the detailed deduction and proof process, refer to Long-quan et al., 2015), then we have:

$$\begin{array}{}\text{(4)}& \begin{array}{rl}& f\left(\mathit{x}\right)=\\ & \left[\begin{array}{l}-{\displaystyle \frac{B_{\text{m}}}{J_{\text{m}}}}{x}_{\mathrm{1}}-{\displaystyle \frac{K}{J_{\text{m}}{N}^{\mathrm{2}}}}{x}_{\mathrm{2}}+{\displaystyle \frac{K}{J_{\text{m}}N}}{x}_{\mathrm{4}}-{\displaystyle \frac{\mathrm{1}}{J_{\text{m}}N}}{x}_{\mathrm{5}}\\ x_{\mathrm{1}}\\ -{\displaystyle \frac{B_{\text{l}}}{J_{\text{l}}}}{x}_{\mathrm{3}}-{\displaystyle \frac{K}{J_{\text{l}}}}{x}_{\mathrm{4}}+{\displaystyle \frac{K}{J_{\text{l}}N}}{x}_{\mathrm{2}}+{\displaystyle \frac{\mathrm{1}}{J_{\text{l}}}}{x}_{\mathrm{5}}\\ {\dot{\mathit{\theta }}}_{\text{l}}\\ -a\mathit{\mu }\ln \left[e^{\frac{\mathrm{1}}{\mathit{\mu }}\left(\frac{x_{\mathrm{1}}}{N}-x_{\mathrm{3}}\right)}+e^{-\frac{\mathrm{1}}{\mathit{\mu }}\left(\frac{x_{\mathrm{1}}}{N}-x_{\mathrm{3}}\right)}\right]q+A\left({\displaystyle \frac{x_{\mathrm{1}}}{N}}-x_{\mathrm{3}}\right)\end{array}\right],\end{array}\end{array}$$

where μ=0.001 and $g\left(\mathit{x}\right)={\left[\mathrm{1},\mathrm{0},\mathrm{0},\mathrm{0},\mathrm{0}\right]}^T$. All the system state variables except q are measurable, and q is a compound function of other state variables. Until this step, one obtain a controllable dynamic model. By measuring state variables of this model, we can create feedback channels to compensate the system for hysteresis torque directly or indirectly. In the following, we will discuss the design of a reasonable controller so that the system output θ_l can track the reference trajectory r in a desired way.

3 Precise State Feedback Linearization and Optimal Controller Design

For the classical optimal control, we need to firstly determine the objective function of the optimal problem. Suppose that the initial conditions of the nonlinear affine system is ${\mathit{x}}_{\mathrm{0}}={\left[\mathrm{0},\mathrm{0},\mathrm{0},\mathrm{0},\mathrm{0}\right]}^T$, the terminal time t_f is fixed and the terminal state x(t_f) is free. Then, the objective function (Anderson et al., 2007) that needs to be minimized is constructed as:

$$\begin{array}{}\text{(5)}& J={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}\int \left[M(r-y{)}^{\mathrm{2}}+R{u}^{\mathrm{2}}\right]\mathrm{d}t,\end{array}$$

where r is the ideal/reference trajectory, y is the actual output of the transmission system, and u denotes the actual control signal. Apparently, it will be very complicated if the Hamiltonian functions are directly constructed by the nonlinear affine system (Eq. 3), which is not convenient for the controller design. Therefore, by using the precise state feedback linearization (Chiasson et al., 1993; Lee et al., 2009) the system can be transformed into a linear one. The time derivatives of the system output y=h(x) are:

$$\begin{array}{}\text{(6)}& \left\{\begin{array}{l}\dot{y}={\displaystyle \frac{\partial h\left(\mathit{x}\right)}{\partial t}}={\displaystyle \frac{\partial h\left(\mathit{x}\right)}{\partial {\mathit{x}}^T}}{\displaystyle \frac{\partial x}{\partial t}}\\ ={\displaystyle \frac{\partial h\left(\mathit{x}\right)}{\partial {\mathit{x}}^T}}\left[f\left(\mathit{x}\right)+g\left(\mathit{x}\right)u\right]=L_{\text{f}}h\left(\mathit{x}\right)+L_{g}h\left(\mathit{x}\right)u,\\ \ddot{y}={\displaystyle \frac{\partial \dot{y}}{\partial t}}={\displaystyle \frac{\partial \dot{y}}{\partial {\mathit{x}}^T}}{\displaystyle \frac{\partial \mathit{x}}{\partial t}}={\displaystyle \frac{\partial \dot{y}}{\partial {\mathit{x}}^T}}\left[f\left(\mathit{x}\right)+g\left(\mathit{x}\right)u\right]\\ =L_{\text{f}}^{\mathrm{2}}h\left(\mathit{x}\right)+L_g{L}_{\text{f}}h\left(\mathit{x}\right)u,\\ \mathrm{\dots }\\ y^{\left(n\right)}={\displaystyle \frac{\partial y^{(n-\mathrm{1})}}{\partial {\mathit{x}}^T}}{\displaystyle \frac{\partial \mathit{x}}{\partial t}}={\displaystyle \frac{\partial L_{\text{f}}^{n-\mathrm{1}}h\left(\mathit{x}\right)}{\partial {\mathit{x}}^T}}\left[f\left(\mathit{x}\right)+g\left(\mathit{x}\right)u\right]\\ =L_{\text{f}}^{n}h\left(\mathit{x}\right)+L_g{L}_{\text{f}}^{n-\mathrm{1}}h\left(\mathit{x}\right)u.\end{array}\right.\end{array}$$

Substituting Eqs. (3)–(5) into the Eq. (6) and expanding the results, it can be observed that the right-hand sides of the first three equations do not explicitly contain u, and $L_g{L}_{\text{f}}^{\mathrm{3}}h\left(\mathit{x}\right)$ contained in the fourth equation is the first nonzero polynomial. Therefore, it is unnecessary to take more than fifth-order derivations The results in Eq. (6) are thus simplified as follows:

$$\begin{array}{}\text{(7)}& \left\{\begin{array}{l}{z}_{\mathrm{1}}=y=x_{\mathrm{4}},\\ z_{\mathrm{2}}=\dot{y}=x_{\mathrm{3}},\\ z_{\mathrm{3}}=\ddot{y}=-{\displaystyle \frac{B_{\text{l}}}{J_{\text{l}}}}{x}_{\mathrm{3}}-{\displaystyle \frac{K}{J_{\text{l}}}}{x}_{\mathrm{4}}+{\displaystyle \frac{K}{J_{\text{l}}N}}{x}_{\mathrm{2}}+{\displaystyle \frac{\mathrm{1}}{J_{\text{l}}}}{x}_{\mathrm{5}},\\ z_{\mathrm{4}}=y^{\left(\mathrm{3}\right)}={\displaystyle \frac{K}{J_{\text{l}}N}}{x}_{\mathrm{1}}\\ \pm {\displaystyle \frac{B_{\text{l}}}{J_{\text{l}}}}\left(-{\displaystyle \frac{B_{\text{l}}}{J_{\text{l}}}}{x}_{\mathrm{3}}-{\displaystyle \frac{K}{J_{\text{l}}}}{x}_{\mathrm{4}}+{\displaystyle \frac{K}{J_{\text{l}}N}}{x}_{\mathrm{2}}+{\displaystyle \frac{\mathrm{1}}{J_{\text{l}}}}{x}_{\mathrm{5}}\right)\\ -{\displaystyle \frac{K}{J_{\text{l}}}}{x}_{\mathrm{3}}+{\displaystyle \frac{\mathrm{1}}{J_{\text{l}}}}\left\{-a\mathit{\mu }\ln \left[e^{\frac{\mathrm{1}}{\mathit{\mu }}\left(\frac{x_{\mathrm{1}}}{N}-x_{\mathrm{3}}\right)}+e^{-\frac{\mathrm{1}}{\mathit{\mu }}\left(\frac{x_{\mathrm{1}}}{N}-x_{\mathrm{3}}\right)}\right]q\right.\\ +A\left({\displaystyle \frac{x_{\mathrm{1}}}{N}}-x_{\mathrm{3}}\right)\mathit{\}},\\ y^{\left(\mathrm{4}\right)}=H\left(\mathit{x}\right)+G\left(\mathit{x}\right)u,\end{array}\right.\end{array}$$

where H(x) equals to:

$$\begin{array}{rl}& H\left(\mathit{x}\right)=\\ & \left({\displaystyle \frac{K}{J_{\text{l}}N}}+{\displaystyle \frac{A}{J_{\text{l}}N}}-{\displaystyle \frac{\mathrm{1}}{J_{\text{l}}N}}aq{\displaystyle \frac{e^{\frac{\mathrm{1}}{\mathit{\mu }}\left(\frac{x_{\mathrm{1}}}{N}-x_{\mathrm{3}}\right)}-e^{-\frac{\mathrm{1}}{\mathit{\mu }}\left(\frac{x_{\mathrm{1}}}{N}-x_{\mathrm{3}}\right)}}{e^{\frac{\mathrm{1}}{\mathit{\mu }}\left(\frac{x_{\mathrm{1}}}{N}-x_{\mathrm{3}}\right)}+e^{-\frac{\mathrm{1}}{\mathit{\mu }}\left(\frac{x_{\mathrm{1}}}{N}-x_{\mathrm{3}}\right)}}}\right)\\ & \left(\begin{array}{l}-{\displaystyle \frac{B_{\text{m}}}{J_{\text{m}}}}{x}_{\mathrm{1}}-{\displaystyle \frac{K}{J_{\text{m}}{N}^{\mathrm{2}}}}{x}_{\mathrm{2}}+\\ {\displaystyle \frac{K}{J_{\text{m}}N}}{x}_{\mathrm{4}}-{\displaystyle \frac{\mathrm{1}}{J_{\text{m}}N}}{x}_{\mathrm{5}}\end{array}\right)-{\displaystyle \frac{B_{\text{l}}K}{J_{\text{l}}^{\mathrm{2}}N}}{x}_{\mathrm{1}}\\ & +\left({\displaystyle \frac{B_{\text{l}}^{\mathrm{2}}}{J_{\text{l}}^{\mathrm{2}}}}-{\displaystyle \frac{K}{J_{\text{l}}}}+{\displaystyle \frac{A{B}_{\text{l}}}{J_{\text{l}}}}-{\displaystyle \frac{\mathrm{1}}{J_{\text{l}}}}aq{\displaystyle \frac{-e^{\frac{\mathrm{1}}{\mathit{\mu }}\left(\frac{x_{\mathrm{1}}}{N}-x_{\mathrm{3}}\right)}+e^{-\frac{\mathrm{1}}{\mathit{\mu }}\left(\frac{x_{\mathrm{1}}}{N}-x_{\mathrm{3}}\right)}}{e^{\frac{\mathrm{1}}{\mathit{\mu }}\left(\frac{x_{\mathrm{1}}}{N}-x_{\mathrm{3}}\right)}+e^{-\frac{\mathrm{1}}{\mathit{\mu }}\left(\frac{x_{\mathrm{1}}}{N}-x_{\mathrm{3}}\right)}}}\right)\\ & \left(\begin{array}{l}-{\displaystyle \frac{B_{\text{l}}}{J_{\text{l}}}}{x}_{\mathrm{3}}-{\displaystyle \frac{K}{J_{\text{l}}}}{x}_{\mathrm{4}}\\ +{\displaystyle \frac{K}{J_{\text{l}}N}}{x}_{\mathrm{2}}+{\displaystyle \frac{\mathrm{1}}{J_{\text{l}}}}{x}_{\mathrm{5}}\end{array}\right)+{\displaystyle \frac{B_{\text{l}}K}{J_{\text{l}}^{\mathrm{2}}}}{x}_{\mathrm{3}}\\ & +\left\{{\displaystyle \frac{B_{\text{l}}}{J_{\text{l}}^{\mathrm{2}}}}-{\displaystyle \frac{\mathrm{1}}{J_{\text{l}}}}a\mathit{\mu }\ln \left[e^{\frac{\mathrm{1}}{\mathit{\mu }}\left(\frac{x_{\mathrm{1}}}{N}-x_{\mathrm{3}}\right)}+e^{-\frac{\mathrm{1}}{\mathit{\mu }}\left(\frac{x_{\mathrm{1}}}{N}-x_{\mathrm{3}}\right)}\right]\right\}\\ & \left\{\begin{array}{l}{\displaystyle \frac{\mathrm{A}}{N}}{x}_{\mathrm{1}}-A{x}_{\mathrm{3}}-\\ a\mathit{\mu }q\ln \left[e^{\frac{\mathrm{1}}{\mathit{\mu }}\left(\frac{x_{\mathrm{1}}}{N}-x_{\mathrm{3}}\right)}+e^{-\frac{\mathrm{1}}{\mathit{\mu }}\left(\frac{x_{\mathrm{1}}}{N}-x_{\mathrm{3}}\right)}\right]\end{array}\right\},\end{array}$$

and G(x) is:

$$\begin{array}{}\text{(8)}& G\left(x\right)={\displaystyle \frac{K}{J_{\text{l}}N}}+{\displaystyle \frac{A}{J_{\text{l}}N}}-{\displaystyle \frac{\mathrm{1}}{J_{\text{l}}N}}aq{\displaystyle \frac{e^{\frac{\mathrm{1}}{\mathit{\mu }}\left(\frac{x_{\mathrm{1}}}{N}-x_{\mathrm{3}}\right)}-e^{-\frac{\mathrm{1}}{\mathit{\mu }}\left(\frac{x_{\mathrm{1}}}{N}-x_{\mathrm{3}}\right)}}{e^{\frac{\mathrm{1}}{\mathit{\mu }}\left(\frac{x_{\mathrm{1}}}{N}-x_{\mathrm{3}}\right)}+e^{-\frac{\mathrm{1}}{\mathit{\mu }}\left(\frac{x_{\mathrm{1}}}{N}-x_{\mathrm{3}}\right)}}}.\end{array}$$

It can be seen that for a nonlinear affine system shown in Eq. (3), if a nonlinear state feedback function, such as $u=\frac{\mathrm{1}}{G\left(\mathit{x}\right)}\left[r-H\left(\mathit{x}\right)\right]$, is appropriately added, the system will degenerate into a quadratic integration system:

$$\begin{array}{}\text{(9)}& y^{\left(\mathrm{4}\right)}=r.\end{array}$$

G(x) is not zero around the initial state ${\mathit{x}}_{\mathrm{0}}=[\mathrm{0},\mathrm{0},\mathrm{0},\mathrm{0},\mathrm{0}{]}^T$ of the transmission system, which means that the precise state feedback linearization is nonsingular around the initial point x₀. Based on Eq. (10), we can design an optimal controller to track the trajectory. Assuming that the objective function of the system is:

$$\begin{array}{}\text{(10)}& J={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}\int \left[M{\left(r-z_{\mathrm{1}}\right)}^{\mathrm{2}}+R{u}_{\mathrm{0}}^{\mathrm{2}}\right]\mathrm{d}t.\end{array}$$

Using the Pontryagin's minimum principle, the Hamiltonian function is obtained:

$$\begin{array}{}\text{(11)}& H={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}M{\left(r-z_{\mathrm{1}}\right)}^{\mathrm{2}}+{\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}R{u}^{\mathrm{2}}+{\mathit{\lambda }}_{\mathrm{1}}{z}_{\mathrm{2}}+{\mathit{\lambda }}_{\mathrm{2}}{z}_{\mathrm{3}}+{\mathit{\lambda }}_{\mathrm{3}}{z}_{\mathrm{4}}+{\mathit{\lambda }}_{\mathrm{4}}{u}_{\mathrm{0}}.\end{array}$$

In terms of the necessary conditions of the optimal control problem, we can obtain the optimal control signal $u_{\mathrm{0}}=-\frac{\mathrm{1}}{R}{\mathit{\lambda }}_{\mathrm{4}}$ and the following equations:

$$\begin{array}{}\text{(12)}& \left\{\begin{array}{l}{\displaystyle \frac{\partial H}{\partial z_{\mathrm{1}}}}=-{\dot{\mathit{\lambda }}}_{\mathrm{1}}=-M\left(r-z_{\mathrm{1}}\right),\\ {\displaystyle \frac{\partial H}{\partial z_{\mathrm{2}}}}=-{\dot{\mathit{\lambda }}}_{\mathrm{2}}={\mathit{\lambda }}_{\mathrm{1}},\\ {\displaystyle \frac{\partial H}{\partial z_{\mathrm{3}}}}=-{\dot{\mathit{\lambda }}}_{\mathrm{3}}={\mathit{\lambda }}_{\mathrm{2}},\\ {\displaystyle \frac{\partial H}{\partial {\mathit{\lambda }}_{\mathrm{1}}}}={\dot{z}}_{\mathrm{1}}=z_{\mathrm{2}},\\ {\displaystyle \frac{\partial H}{\partial {\mathit{\lambda }}_{\mathrm{2}}}}={\dot{z}}_{\mathrm{2}}=z_{\mathrm{3}},\\ {\displaystyle \frac{\partial H}{\partial {\mathit{\lambda }}_{\mathrm{3}}}}={\dot{z}}_{\mathrm{3}}=z_{\mathrm{4}},\\ {\displaystyle \frac{\partial H}{\partial {\mathit{\lambda }}_{\mathrm{4}}}}={\dot{z}}_{\mathrm{4}}=u_{\mathrm{0}}=-{\displaystyle \frac{\mathrm{1}}{R}}{\mathit{\lambda }}_{\mathrm{4}}.\end{array}\right.\end{array}$$

The boundary conditions are:

$$\begin{array}{}\text{(13)}& \mathit{\lambda }=\left[\begin{array}{c}{\mathit{\lambda }}_{\mathrm{1}}\left(t_{\text{f}}\right)\\ {\mathit{\lambda }}_{\mathrm{2}}\left(t_{\text{f}}\right)\\ {\mathit{\lambda }}_{\mathrm{3}}\left(t_{\text{f}}\right)\\ {\mathit{\lambda }}_{\mathrm{4}}\left(t_{\text{f}}\right)\end{array}\right]=\left[\begin{array}{c}\mathrm{0}\\ \mathrm{0}\\ \mathrm{0}\\ \mathrm{0}\end{array}\right].\end{array}$$

Here, the control signal u₀ is determined by the co-state variable λ, reference input r and system feedback z₁. It is clear that the control signal is independent of the actual structure of the object system. Therefore, by using the following control signal

$$\begin{array}{}\text{(14)}& u={\displaystyle \frac{\mathrm{1}}{G\left(\mathit{x}\right)}}\left[u_{\mathrm{0}}-H\left(\mathit{x}\right)\right],\end{array}$$

and also substituting Eq. (6) into Eq. (13), we have:

$$\begin{array}{}\text{(15)}& \left\{\begin{array}{l}-{\dot{\mathit{\lambda }}}_{\mathrm{1}}=-M\left(r-{\mathit{\theta }}_{\text{l}}\right),\\ -{\dot{\mathit{\lambda }}}_{\mathrm{2}}={\mathit{\lambda }}_{\mathrm{1}},\\ -{\dot{\mathit{\lambda }}}_{\mathrm{3}}={\mathit{\lambda }}_{\mathrm{2}},\\ -{\dot{\mathit{\lambda }}}_{\mathrm{4}}={\mathit{\lambda }}_{\mathrm{3}},\\ {\ddot{\mathit{\theta }}}_{\text{m}}=-{\displaystyle \frac{B_{\text{m}}}{J_{\text{m}}}}{x}_{\mathrm{1}}-{\displaystyle \frac{K}{J_{\text{m}}{N}^{\mathrm{2}}}}{x}_{\mathrm{2}}+{\displaystyle \frac{K}{J_{\text{m}}N}}{x}_{\mathrm{4}}-{\displaystyle \frac{\mathrm{1}}{J_{\text{m}}N}}{x}_{\mathrm{5}}\\ +{\displaystyle \frac{\mathrm{1}}{G\left(x\right)}}\left[-{\displaystyle \frac{\mathrm{1}}{R}}{\mathit{\lambda }}_{\mathrm{4}}-H\left(\mathit{x}\right)\right],\\ {\dot{\mathit{\theta }}}_{\text{m}}=x_{\mathrm{1}},\\ {\ddot{\mathit{\theta }}}_{\text{l}}={\displaystyle \frac{B_{\text{l}}}{J_{\text{l}}}}{x}_{\mathrm{3}}-{\displaystyle \frac{K}{J_{\text{l}}}}{x}_{\mathrm{4}}+{\displaystyle \frac{K}{J_{\text{l}}N}}{x}_{\mathrm{2}}+{\displaystyle \frac{\mathrm{1}}{J_{\text{l}}}}{x}_{\mathrm{5}},\\ \dot{q}=-a\mathit{\mu }\ln \left[e^{\frac{\mathrm{1}}{\mathit{\mu }}\left(\frac{x_{\mathrm{1}}}{N}-x_{\mathrm{3}}\right)}+e^{-\frac{\mathrm{1}}{\mathit{\mu }}\left(\frac{x_{\mathrm{1}}}{N}-x_{\mathrm{3}}\right)}\right]x_{\mathrm{5}}\\ +A\left({\displaystyle \frac{x_{\mathrm{1}}}{N}}-x_{\mathrm{3}}\right).\end{array}\right.\end{array}$$

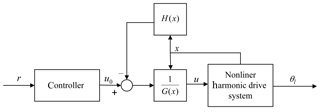
Equation (16) include both the initial-value and boundary-value constraints, namely a complex boundary value problem (BVP) in which numerical methods are needed to solve the equations (Shampine et al., 2000; Ascher et al., 1994). In terms of Eq. (16), the simulation system is constructed, as shown in Fig. 4.

Figure 4 Simplified block diagram of the control system constructed according to Eq. (16).

The simulation steps of the control system are as follows:

• First, calculate the input signal based on the pre-designed trajectories r and Eq. (16). The state variable of the controller is the co-state variable λ.

• Then, using the feedback channel, calculate the nonlinear feedback signal by measuring the state variable of the transmission system.

• Finally, combining the output signal of the controller with the nonlinear feedback signal and importing them into the transmission system, obtain the desired trajectory at the output of the harmonic drive.

4 Simulations

In order to illustrate the superiority of the new compound controller proposed, in this section, we compare the control performance of the present compound controller with the control method of disturbance observer based control (DOBC) (Yang et al., 2011). The main control idea of DOBC is that the hysteresis torques $-\frac{\mathrm{1}}{J_{\text{m}}N}q$ and $\frac{\mathrm{1}}{J_{\text{l}}}q$ are treated as interferences so as to realize real-time compensation, which makes the resulting system become linear, i.e.:

$$\begin{array}{}\text{(16)}& \left\{\begin{array}{l}\dot{\mathit{x}}=\mathbf{A}\mathit{x}+\mathbf{B}\mathit{u}+\mathbf{C}\mathit{d},\\ \mathit{y}=\mathbf{D}\mathit{x},\end{array}\right.\end{array}$$

where d=q, and

$$\mathbf{C}=\left[\begin{array}{cccc}-{\displaystyle \frac{\mathrm{1}}{J_{\text{m}}N}}& \mathrm{0}& \mathrm{0}& \mathrm{0}\\ \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}\\ \mathrm{0}& \mathrm{0}& {\displaystyle \frac{\mathrm{1}}{J_{\text{l}}}}q& \mathrm{0}\\ \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}\end{array}\right]$$

The observer is defined as:

$$\begin{array}{}\text{(17)}& \left\{\begin{array}{l}\dot{\mathit{z}}=-\mathbf{L}C\left(\mathit{z}+L\mathit{x}\right)-\mathbf{L}\left(\mathbf{A}\mathit{x}+\mathbf{B}\mathit{u}\right),\\ \widehat{\mathit{d}}=\mathit{z}+\mathbf{L}\mathit{x},\\ \mathit{u}={\mathbf{K}}_x\left(\mathit{r}-\mathit{x}\right)+{\mathbf{K}}_d\widehat{\mathit{d}},\end{array}\right.\end{array}$$

where K_x and K_d are feedback gains. The parameters of the observer are:

$$\mathbf{L}=\left[\begin{array}{cccc}\mathrm{40}& \mathrm{0}& \mathrm{0}& \mathrm{0}\\ \mathrm{0}& \mathrm{40}& \mathrm{0}& \mathrm{0}\\ \mathrm{0}& \mathrm{0}& \mathrm{40}& \mathrm{0}\\ \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{40}\end{array}\right]$$

In Eq. (18), in order to meet the stability requirement, the feedback gains, K_x and K_d, must be Hurwitz matrices with K_d determined by K_x and L (Li et al., 2014). Therefore, in this study, classical linear quadratic regulator (LQR) with positive definite penalty matrices, Q and R, is adopted to meet the stability requirement of K_x. For cost function of LQR, we select R=0.001 and

$$\mathbf{Q}=\left[\begin{array}{cccc}\mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}\\ \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}\\ \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}\\ \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{1000}\end{array}\right]$$

Then, we can obtain the controller's gains ${\mathbf{K}}_x=[-\mathrm{0.1469},-\mathrm{37.2786},-\mathrm{0.2057},\mathrm{863.9319}]$ and ${\mathbf{K}}_d=[-\mathrm{0.02},\mathrm{0},-\mathrm{0.2803},\mathrm{0}]$.

For the compound optimal control proposed in this paper, there are only two controllable parameters, namely M and R. We can adjust the two parameters to improve the tracking performance of the control system. The rest of the parameters are listed in the Table 1. Numerical simulations show that the smaller R is, the larger the amplitude of the control signal is. By adjusting M, we can also amplify the control signal. It is also noted that if R is too small, the numerical method will fail to solve the complex BVP (Eq. 16). However, an optimal allowable R can be found to satisfy the tracking precision. So we choose M=10 000 and R=0.001. Once the parameters used in DOBC controller and the compound optimal controller have been confirmed, one can compare their control performances by tracking the same reference trajectory $r=\mathrm{1}-\cos \left(\mathit{\pi }t\right)$.

Table 1 The Inherent Parameters of Harmonic Drive System (Gandhi et al., 2001).

5 Results and Discussions

The response curves of DOBC and the compound optimal control together with the reference trajectory are shown in Fig. 5. It is observed that the steady-state tracking of the present compound optimal control method is excellent. For DOBC, however, there is always a large tracking error around the peak of the trajectory curve, which means that the tracking curve cannot follow the reference as desired. This is because the proportional control in DOBC cannot completely get rid of the static error in the closed-loop system.

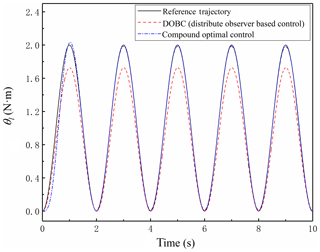
Figure 5 The cosine wave tracking effect of the compound optimal control and DOBC. The tracking curve of the compound optimal control almost overlaps with the reference trajectory.

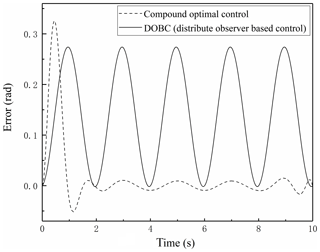
The tracking errors between the reference trajectory and each of the two controlled trajectories are illustrated in Fig. 6. In this case, the reference trajectory is a cosine wave with maximum amplitude of one. For a serial transmission system whose initial state is stationary, both of the controllers mentioned above can enter the steady-state tracking within 1 second by properly designing the desired trajectory. It is found that when the system reaches the steady state, the maximum relative error from the compound optimal control reduces to less than 1 %, while that from DOBC fluctuates periodically within 25 %. Therefore, compared with DOBC, the compound optimal control can realize a stable tracking with a much better precision control.

Figure 6 Tracking error of DOBC and the compound optimal control.

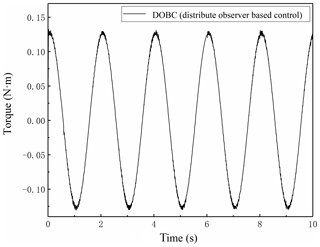
Control signals of DOBC and compound optimal control are shown in Figs. 7 and 8, respectively. As shown in Fig. 7, although DOBC system enters a relatively steady state in general, the control signal is still mixed with a large number of high-frequency components around the peak and valley points of the curve. These high-frequency components result from the linear observer used in estimating hysteresis torque. It is clear that the angular speeds of the harmonic driver and motor change sharply around the peak and valley of the trajectory curve, meaning that the angular accelerations are maximum at the peak and valley points. Meanwhile, it is already known from Eq. (2) that the hysteresis torque is sensitive to the angular speed difference between the harmonic drive and the motor. This indicates that the control signal of DOBC inherently contains massive high-frequency components when tracking complex trajectories. With the increase of the frequency of the reference wave, more high-frequency components can appear. That may be the reason why DOBC is mostly used in the constant speed regulation of the permanent magnet synchronous motor (PMSM) instead of accurate trajectory tracking. In the relevant experimental literatures, find similar phenomenon can be found. For example, Lu et al. (2016) built a load DOBC (LDOBC) to estimate the disturbance on load side and realized the trajectory tracking of permanent magnet synchronous machine (PMSM). However, the friction inside the PMSM increases when the motor speed is faster. Their experimental results showed that the high-frequency components in the input signal and output signal increased when the rotate speed increased from 100 to 2500 rotations per minute. This agrees well with our simulation results.

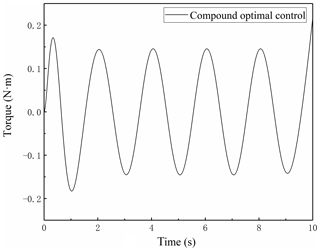
The control signal of the present compound optimal control in Fig. 8 behaves much smoother and its initial value is zero. Noticeably, the optimal controller eliminates the high-frequency components as seen in DOBC. This resulting control signal requires less bandwidth of the servomotor and lead to more benefit for the stationary-state startup of the servomotor. The control signal of the present controller contains no high-frequency components when increasing the frequency of the reference cosine wave. Compared with DOBC, the compound optimal control is more adaptive for tracking the complex trajectory with desired precision.

Figure 7 The input torque curve of DOBC.

In summary, unlike DOBC which is a closed-loop control based on the real-time feedback, the compound optimal controller is an open-loop control. Although the compound optimal control requires solving the complex BVP equations in advance, the control signal quality and the control effect are much better than those of DOBC. In addition, there are only two parameters (M and R) in the compound optimal control, which can be easily adjusted to meet different requirements.

These numerical cases demonstrate that the new compound optimal controller presented in this paper has a better comprehensive performance in dealing with hysteresis issue.

6 Conclusions

The present work focuses on the improvement of the tracking accuracy of the motor-harmonic drive serial system considering the influence of hysteresis torque and a compound optimal control scheme for a harmonic drive has been established. The main results are summarized as follows.

Figure 8 The torque curve of the compound optimal control signal Eq. (15).

By means of coordinate transformation and precise state feedback linearization, the original nonlinear system is transformed into a fourth-order integral system, in which the non-differentiable structure of the original system (such as the absolute value function) is approximated by the equivalent smooth function. The new control system is not only beneficial to the design of the controller, but also has no singularity around the initial state ${\mathit{x}}_{\mathrm{0}}={\left[\mathrm{0},\mathrm{0},\mathrm{0},\mathrm{0},\mathrm{0}\right]}^T$.

A compound open-loop optimal controller based on a linear quadratic regulator is designed for tracking the expected trajectory of the harmonic drive with hysteresis behavior. In this control method, the quadratic optimal state regulator is employed to quantify the whole tracking precision of the control system. In order to get the actual control torque according to the desired trajectory and boundary value, it requires to solve the complex BVP equations in advance. Compared with the traditional control methods, the present compound optimal controller can achieve an optimal performance and is more adaptive for tracking the complex trajectory with desired precision.

Simulation results reveal that when tracking the complex trajectory like cosine wave with similar responding speed, the relative error from DOBC based on linear observer fluctuates between 0 % and 25 %. However, for the new compound optimal controller, the relative error of the steady state can be smaller than 1 % and no periodic fluctuation phenomenon appears. In addition, the compound optimal controller can eliminate the high-frequency components that appear in DOBC. In other words, the control signal curve of the compound optimal controller is much smoother and more suitable for the torque output of the actual servomotor, than that of DOBC.

Further work is planned on improving the ability of noise resistance and reducing the computational complexity of this new controller. In doing this, we can extend the optimization problem to the robust control problem where the online optimal control becomes necessary.