Nonlinear Dynamic Analysis of high speed multiple units Gear Transmission System with Wear Fault

The helical gear system is an important form of transmission in high-speed trains, and helical gear failure has a great impact on the transmission performance. To investigate the influence of wear parameters on the nonlinear dynamics of gear systems, the wear fault parameters of a bending-torsion-shaft coupling mode with six degrees of freedom are established. Using the variable step fourth-order Runge-Kutta numerical integration method, the gear dynamics model with fault parameters is analyzed to get the dynamic response of the helical gear system. The system excitation frequency, evolution of system periodic motion, quasi-periodic motion, and chaotic motion with variable fault parameters are analyzed qualitatively based on the results, including the system status judgment criteria of phase plane graph, Poincaré cross-section graph, bifurcation diagram, and RMS. The results show that wear fault affects the system differently at different frequencies. Finally, the correctness of the conclusion is verified through experiments, and the impact on the actual application process is analyzed.

1 Introduction

Helical gears are not only a common transmission mecha-nism but also an important form of transmission in high-speed trains. Their reliability is thus important for the overall industrial processes (Wang et al., 2018). The high-speed train gear-box-driven gear is directly press-fitted on the axle, and the driving gear is connected with the traction motor through coupling and hangs on the cross beam through the gear box (Zhang, 2011). Therefore, the vibration characteristics of the gear system will directly affect the running performance of the high-speed train and the drive transmission system.

In recent years, many scholars have studied the non-linear dynamics of gear systems. Spitas and Spitas (2015) analyzed a coupled multi-DOF dynamic contact model with intermittent gear tooth contacts. Wang et al. (2011) made a preliminary analysis of a fault gear simulation method. Ma and Chen (2012) established a torsional gear pair model and analyzed the singularity of cracked gear and the dynamic response process of crack evolution. Zhang et al. (2011) took into account the dynamic distribution of load in the meshing area and the use of gear test standards and tolerances to determine the transmission error of gear pairs in the study of gear transmission system with tooth root crack failure. Parey and Tandon (2003) and Parey et al. (2006) established a variety of fault gear dynamics models and response signal analyses in the study of gear system dynamics with defects. Alshyyab and Kahraman et al. (2005) studied a kind of discrete Fourier transform of nonlinear time-varying kinetics models using the multiple harmonic balance method and found that stable subharmonic waves exist mainly in the form of softening. Chaari et al. (2009) quantified the reduction of meshing stiffness caused by partial failure of gears and proposed a finite element model to verify the analytical formula. Kahraman and Singh (1991) studied the frequency-response characteristics of nonlinear gear rotor-bearing systems with time-varying mesh stiffness. Shen et al. (2006) extended the incremental harmonic balance method to the nonlinear dynamic analysis of gear pairs. Rao et al. (2014) studied the torsional vibration characteristics of two-stage spur gear systems. The above studies mainly focused on the crack evolution and resonance response of faulty gears. Although there are many studies of normally operating spur gear transmission systems, there are fewer studies on the failure of helical gear transmissions system. In addition, there are few studies on the dynamic characteristics of helical gear systems with high-speed train fault parameters.

In this paper, the faulty helical gear of a high-speed train is taken as the research object, and time-varying pa-rameters, time-varying mesh stiffness, and time-varying mesh error are fully considered. The bending-torsion-axis coupling system model of the faulty helical gear is established. Through numerical analysis of the dynamic model combined with the phase diagram, Poincaré section map, bifurcation diagram, and spectrogram of the response of the nonlinear gear system, the dynamic response of the gear transmission system under wear fault is qualitatively analyzed.

2 Six Degrees of Freedom Dynamics Model of Helical Gear System

2.1 Mechanical model of gear system and differential equations of motion

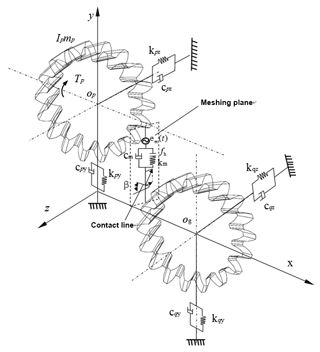
The gear transmission systems of high-speed trains adopt helical gear transmission. In the process of transmission, the meshing of gears generates axial dynamic meshing force, so the transmission system has torsional vibration, lateral vibration, and axial vibration, thus forming a meshing type of bending-torsion-shaft coupling system dynamics mode (Li and Wang, 1999). Accordingly, the establishment of a high-speed train helical gear transmission dynamics model is shown in Fig. 1. The system is a three-dimensional vibration model. To simplify calculation, this model does not consider friction of tooth surface and contains six degrees of freedom. In Fig. 1, O_p and O_g represent the centroids of the driving and driven gears, respectively; m_p and m_g represent mass; R_p and R_g represent the radius of the base circle; I_p and I_g represent the moment of inertia; k_py and k_gy represent stiffness in the tangential direction; k_pz and k_gz represent stiffness in the axial direction; c_py and c_gy represent damping in the tangential direction; k_m and c_m represent gear meshing stiffness and damping factors, respectively; f_h represents the gear meshing displacement function; T_p represents the external load torque on the driving wheel; T_g represents the output torque; and β is the tilt angle of gears.

Figure 1 Three-dimensional vibration model of gear system.

According to Newton's second law, the analytical model of the gear system in Fig. 1 can be deduced as follows:

$$\begin{array}{}\text{(1)}& {\displaystyle }\left\{\begin{array}{l}{m}_p\ddot{y_{\text{p}}}+c_{py}\dot{y_{\text{p}}}+k_{py}{f}_y\left(y_{\text{p}}\right)=-F_y\\ m_g\ddot{y_{\text{g}}}+c_{gy}\dot{y_{\text{g}}}+k_{gy}{f}_y\left(y_{\text{g}}\right)=F_y\\ m_p\ddot{z_p}+c_{pz}\dot{z_{\text{p}}}+k_{pz}{f}_z\left(z_{\text{p}}\right)=-F_z\\ m_g\ddot{z_{\text{g}}}+c_{gz}\dot{z_{\text{g}}}+k_{gz}{f}_z\left(z_{\text{g}}\right)=F_z\\ I_p\ddot{{\mathit{\theta }}_p}=T_p-F_y{R}_P\\ I_g\ddot{{\mathit{\theta }}_{\text{g}}}=-T_g+F_g{R}_P\end{array}\right.\end{array}$$

In Eq. (1), F_y and F_z represent the tangential and axial dynamic engagement forces, respectively, and they can be expressed as follows:

$$\begin{array}{ll}{\displaystyle }{F}_z=& {\displaystyle }\sin b\mathit{\{}{k}_{\mathrm{m}}{f}_z\left[z_{\text{p}}-tgb(y_{\text{p}}+q_p{R}_p)-z_{\text{g}}\right.\\ {\displaystyle }& {\displaystyle }\left.+tgb(y_{\text{g}}+q_g{R}_g)-e_m\left(t\right)\sin b\right]\\ {\displaystyle }& {\displaystyle }+c_{\mathrm{m}}\left[\dot{z_{\text{p}}-tgb}(\dot{y_{\text{p}}}+\dot{q_p}{R}_p)\right.\\ \text{(2)}& {\displaystyle }& {\displaystyle }\left.-\dot{z_{\text{g}}}-tgb(\dot{y_{\text{g}}}+\dot{q_g}{R}_g)-\dot{e_m\left(t\right)}\sin b\right]\mathit{\}}\end{array}$$

$$\begin{array}{ll}{\displaystyle }{F}_y=& {\displaystyle }\cos \mathit{\beta }\left[k_{\mathrm{m}}{f}_y\left(y_{\text{p}}+{\mathit{\theta }}_p{R}_p-y_{\text{g}}+{\mathit{\theta }}_{\text{g}}{R}_g\right.\right.\\ {\displaystyle }& {\displaystyle }\left.-e_m\left(t\right)\cos \mathit{\beta }\right)+c_{\mathrm{m}}\left(\dot{y_{\text{p}}}+\dot{{\mathit{\theta }}_p}{R}_p-\dot{y_{\text{g}}}\right.\\ \text{(3)}& {\displaystyle }& {\displaystyle }\left.\left.+\dot{{\mathit{\theta }}_{\text{g}}}{R}_g-e_m\dot{(}t)\cos \mathit{\beta }\right)\right]\end{array}$$

In Eqs. (2) and (3), “^.” represents taking the derivative for t; y_p and z_p represent the panning vibration displacement of the main driven gear in the y direction, y_g and z_g represent the panning vibration displacement of the main driven gear in the z direction; and θ_p and θ_g represent the corner vibration displacement of the main gear and driven gear.

After that, make the Eq. (1) dimensionless; add the gear pair gap length b; assume ${\mathit{\zeta }}_{\mathrm{1}}=y_{\mathrm{p}}/b$, ${\mathit{\zeta }}_{\mathrm{2}}=y_{\mathrm{g}}/b$, ${\mathit{\zeta }}_{\mathrm{3}}=z_{\mathrm{p}}/b$, ${\mathit{\zeta }}_{\mathrm{4}}=z_{\mathrm{g}}/b$ and ${\mathit{\zeta }}_{\mathrm{5}}=({\mathit{\theta }}_p{R}_p-{\mathit{\theta }}_{\mathrm{g}}{R}_g)/b$; define the tangential relative displacement of the gear system as y₁ , and define the axial relative displacement as y₂ (Wu et al., 2016). Then:

$$\begin{array}{}\text{(4)}& {\displaystyle }& {\displaystyle }{y}_{\mathrm{1}}={\mathit{\zeta }}_{\mathrm{1}}-{\mathit{\zeta }}_{\mathrm{2}}+{\mathit{\zeta }}_{\mathrm{5}}-e_m\left(t\right)/b,\text{(5)}& {\displaystyle }& {\displaystyle }{y}_{\mathrm{2}}={\mathit{\zeta }}_{\mathrm{3}}-{\mathit{\zeta }}_{\mathrm{4}}-tg\mathit{\beta }({\mathit{\zeta }}_{\mathrm{1}}-{\mathit{\zeta }}_{\mathrm{2}}+{\mathit{\zeta }}_{\mathrm{5}})-e_m\left(t\right)/b,\text{(6)}& {\displaystyle }& {\displaystyle }\mathit{\tau }=w_{\mathrm{n}}t,\text{(7)}& {\displaystyle }& {\displaystyle }{w}_{\mathrm{n}}=\sqrt{k_{\mathrm{m}}/m_{\mathrm{e}}},\text{(8)}& {\displaystyle }& {\displaystyle }{m}_{\mathrm{e}}={\displaystyle \frac{I_{\mathrm{1}}{I}_{\mathrm{2}}}{I_{\mathrm{1}}{R}_{\mathrm{2}}^{\mathrm{2}}+I_{\mathrm{2}}{R}_{\mathrm{1}}^{\mathrm{2}}}},\text{(9)}& {\displaystyle }& {\displaystyle }w=w_p/w_{\mathrm{n}},\end{array}$$

In the above equations, τ represents unit time after dimensionless processing; w_n represents the gear's natural frequency; and m_e represents the gear's equivalent mass.

Combine the last two torsional dynamics equations, and define the non-dimensional internal excitation frequency $w=w_p/w_{\mathrm{n}}$. The non-dimensional system dynamics equations are obtained from Eq. (1):

$$\begin{array}{}\text{(10)}& \left\{\begin{array}{l}{\mathit{\zeta }}_{\mathrm{1}}\ddot{+}\mathrm{2}{\mathit{\eta }}_{\mathrm{11}}{\mathit{\zeta }}_{\mathrm{1}}\dot{+}{K}_{\mathrm{11}}{\mathit{\zeta }}_{\mathrm{1}}=-\cos \mathit{\beta }\left[K_{\mathrm{10}}{f}_y\right(y_{\mathrm{1}})+\mathrm{2}{\mathit{\epsilon }}_{\mathrm{10}}{y}_{\mathrm{1}}\dot{]},\\ {\mathit{\zeta }}_{\mathrm{2}}\ddot{+}\mathrm{2}{\mathit{\eta }}_{\mathrm{21}}{\mathit{\zeta }}_{\mathrm{2}}\dot{+}{K}_{\mathrm{21}}{\mathit{\zeta }}_{\mathrm{2}}=\cos \mathit{\beta }\left[K_{\mathrm{20}}{f}_y\right(y_{\mathrm{1}})+\mathrm{2}{\mathit{\epsilon }}_{\mathrm{20}}{y}_{\mathrm{1}}\dot{]},\\ {\mathit{\zeta }}_{\mathrm{3}}\ddot{+}\mathrm{2}{\mathit{\eta }}_{\mathrm{12}}{\mathit{\zeta }}_{\mathrm{3}}\dot{+}{K}_{\mathrm{12}}{\mathit{\zeta }}_{\mathrm{3}}=-\sin \mathit{\beta }\left[K_{\mathrm{10}}{f}_z\right(y_{\mathrm{2}})+\mathrm{2}{\mathit{\epsilon }}_{\mathrm{10}}{y}_{\mathrm{2}}\dot{]},\\ {\mathit{\zeta }}_{\mathrm{4}}\ddot{+}\mathrm{2}{\mathit{\eta }}_{\mathrm{22}}{\mathit{\zeta }}_{\mathrm{4}}\dot{+}{K}_{\mathrm{22}}{\mathit{\zeta }}_{\mathrm{4}}=\sin \mathit{\beta }\left[K_{\mathrm{20}}{f}_z\right(y_{\mathrm{2}})+\mathrm{2}{\mathit{\epsilon }}_{\mathrm{20}}{y}_{\mathrm{2}}\dot{]},\\ {\mathit{\zeta }}_{\mathrm{5}}\ddot{+}\cos \mathit{\beta }\left[K_{\mathrm{0}}{f}_y\right(y_{\mathrm{1}})+\mathrm{2}{\mathit{\epsilon }}_{\mathrm{0}}{y}_{\mathrm{1}}\dot{]}=F{K}_{\mathrm{30}}/b.\end{array}\right.\end{array}$$

In Eq. (10), the variables are defined as follows:

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }{\mathit{\eta }}_{\mathrm{11}}={\displaystyle \frac{c_{py}}{\mathrm{2}{m}_p{w}_{\mathrm{n}}}}{K}_{\mathrm{11}}={\displaystyle \frac{k_{py}}{m_p{w}_{\mathrm{n}}^{\mathrm{2}}}}\\ {\displaystyle }& {\displaystyle }{\mathit{\epsilon }}_{\mathrm{10}}={\displaystyle \frac{c_m}{\mathrm{2}{m}_p{w}_{\mathrm{n}}}}{\mathit{\eta }}_{\mathrm{21}}={\displaystyle \frac{c_{qy}}{\mathrm{2}{m}_q{w}_{\mathrm{n}}}}\\ {\displaystyle }& {\displaystyle }{K}_{\mathrm{21}}={\displaystyle \frac{k_{qy}}{m_q{w}_{\mathrm{n}}^{\mathrm{2}}}}{\mathit{\epsilon }}_{\mathrm{20}}={\displaystyle \frac{c_m}{\mathrm{2}{m}_q{w}_{\mathrm{n}}}}\\ {\displaystyle }& {\displaystyle }{\mathit{\eta }}_{\mathrm{12}}={\displaystyle \frac{c_{pz}}{\mathrm{2}{m}_p{w}_{\mathrm{n}}}}{K}_{\mathrm{12}}={\displaystyle \frac{k_{pz}}{m_p{w}_{\mathrm{n}}^{\mathrm{2}}}}\\ {\displaystyle }& {\displaystyle }{K}_{\mathrm{10}}={\displaystyle \frac{k_m}{m_p{w}_{\mathrm{n}}^{\mathrm{2}}}}{\mathit{\eta }}_{\mathrm{22}}={\displaystyle \frac{c_{qz}}{\mathrm{2}{m}_q{w}_{\mathrm{n}}}}\\ {\displaystyle }& {\displaystyle }{K}_{\mathrm{22}}={\displaystyle \frac{k_{qz}}{m_q{w}_{\mathrm{n}}^{\mathrm{2}}}}{K}_{\mathrm{20}}={\displaystyle \frac{k_m}{m_q{w}_{\mathrm{n}}^{\mathrm{2}}}}\\ {\displaystyle }& {\displaystyle }{K}_{\mathrm{0}}={\displaystyle \frac{k_m}{m_{\mathrm{e}}{w}_{\mathrm{n}}^{\mathrm{2}}}}{\mathit{\epsilon }}_{\mathrm{0}}={\displaystyle \frac{c_m}{\mathrm{2}{m}_{\mathrm{e}}{w}_{\mathrm{n}}}}\\ {\displaystyle }& {\displaystyle }{K}_{\mathrm{30}}={\displaystyle \frac{\mathrm{1}}{m_{\mathrm{e}}{w}_{\mathrm{n}}^{\mathrm{2}}}}F={\displaystyle \frac{T_p}{R_p}}={\displaystyle \frac{T_q}{R_q}}\end{array}$$

The basic parameters of gear pairs used in this paper are shown in Table 1.

Table 1 A certain type of high-speed train helical gear basic parameters.

2.2 Gear time-varying mesh stiffness

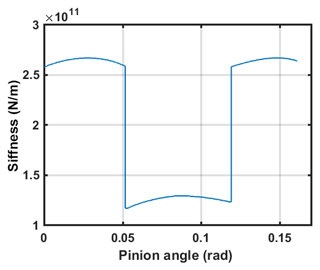
The stiffness excitation is a kind of dynamic excitation, which is formed due to the change of integrated stiffness with time in the gear meshing process. With the constant alternating of double teeth and multiple teeth meshing, the bearing load and elastic deformation between gears will alternate. Due to the tilt angle, the helical gears experience a reduced amount of abrupt change in the alternating changes of tooth pairs. However, considering the irregularity of contact line and interaction of multiple teeth, as well as the presence of manufacturing errors, there are also periodic changes in elastic deformation and meshing stiffness. Using the accumulated integral potential energy method (Wan et al., 2015), the curve of time-varying mesh stiffness is shown in Fig. 2.

Figure 2 Time-varying mesh stiffness curve.

The gear meshing stiffness varies with meshing position. When a pair of gears meshes at the meshing point j, the gear meshing stiffness can be expressed as:

$$\begin{array}{}\text{(11)}& k_j={\displaystyle \frac{\mathrm{1}}{\frac{\mathrm{1}}{k_{bj\mathrm{1}}}+\frac{\mathrm{1}}{k_{bj\mathrm{2}}}+\frac{\mathrm{1}}{k_{fj\mathrm{1}}}+\frac{\mathrm{1}}{k_{fj\mathrm{2}}}+\frac{\mathrm{1}}{k_{hj}}}},\end{array}$$

where the subscript numbers 1 and 2 represent the driving wheel and the driven wheel, respectively; k_bj1 and k_bj2 represent the stiffness corresponding to the bending, shearing, and compression deformation of the teeth; k_fj1 and k_fj2 represent the stiffness corresponding to the deformation of the gear; and k_hj is the stiffness corresponding to the Hertz contact deformation. During the involute gear meshing process, single and double teeth alternately appear, and a complete meshing period is divided into two parts: single tooth meshing and double tooth meshing. When the double teeth are engaged, the meshing stiffness is a superposition of the meshing stiffness of the two pairs of teeth. The gear meshing stiffness in a complete meshing cycle can be determined by ascertaining the single tooth meshing zone and the double tooth meshing zone from the gear geometry.

The teeth are divided into n micro-elements, and the portion connected to the micro-element close to the crest is regarded as a rigid body. The cross-section of each micro-element is rectangular. It is assumed that the thickness of each micro-element is L_i, the cross-sectional area is A_i, the cross-sectional area moment is I_i , the distance from the micro-element to the meshing point is S_ij, the pressure angle corresponding to the meshing point is α_j, and the distance between the meshing point and the neutral layer of the tooth is Y_j. According to the theory of Timoshinko beam, the stiffness corresponding to the bending, shearing, and compression deformation of the teeth is (Li and Wang, 1999):

$$\begin{array}{ll}{\displaystyle }{k}_{bj}=& {\displaystyle }\left[\sum _{i=\mathrm{1}}^n{\displaystyle \frac{\mathrm{1}}{E_e}}\left({\displaystyle \frac{L_i^{\mathrm{3}}+\mathrm{3}{L}_i^{\mathrm{2}}{S}_{ij}+\mathrm{3}{L}_i{S}_{ij}^{\mathrm{2}}}{\mathrm{3}{I}_i}}{\cos }^{\mathrm{2}}{\mathit{\alpha }}_j\right.\right.\\ {\displaystyle }& {\displaystyle }-{\displaystyle \frac{L_i^{\mathrm{2}}+\mathrm{2}{L}_i{Y}_{ij}{S}_{ij}}{\mathrm{2}{I}_i}}{\cos }^{\mathrm{2}}{\mathit{\alpha }}_j\\ \text{(12)}& {\displaystyle }& {\displaystyle }{\left.\left.+{\displaystyle \frac{(\mathrm{12}+\mathrm{11}v)L_i}{\mathrm{5}{A}_i}}{\cos }^{\mathrm{2}}{\mathit{\alpha }}_j+{\displaystyle \frac{L_i}{A_i}}{\sin }^{\mathrm{2}}{\mathit{\alpha }}_j\right)\right]}^{-\mathrm{1}},\end{array}$$

Sainsot (Sainsot et al., 2004) proposed that the stiffness corresponding to the deformation of the involute spur gear based on the Muskhelishvili elastic ring theory can be expressed as:

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }{k}_{ff}=\\ \text{(13)}& {\displaystyle }& {\displaystyle }{\left[{\displaystyle \frac{{\cos }^{\mathrm{2}}{\mathit{\alpha }}_i}{B{E}_e}}\left(L^{\ast }{\displaystyle \frac{u_f^{\mathrm{2}}}{S_f^{\mathrm{2}}}}+M^{\ast }{\displaystyle \frac{u_f}{S_f}}+P^{\ast }(\mathrm{1}+Q^{\ast }\tan {\mathit{\alpha }}_i)\right)\right]}^{-\mathrm{1}},\end{array}$$

The parameters in Eq. (13) are shown in Sainsot et al. (2004).

The stiffness corresponding to the Hertzian contact deformation of a pair of teeth on meshing line is constant, and it is expressed as (Yang and Sun, 1985):

$$\begin{array}{}\text{(14)}& {\displaystyle }{k}_{hj}={\left[{\displaystyle \frac{\mathrm{2}}{\mathit{\pi }B}}\left({\displaystyle \frac{\mathrm{1}-v_{\mathrm{1}}^{\mathrm{2}}}{E_{\mathrm{1}}}}+{\displaystyle \frac{\mathrm{1}-v_{\mathrm{2}}^{\mathrm{2}}}{E_{\mathrm{2}}}}\right)\right]}^{-\mathrm{1}},\end{array}$$

where B is the actual contact tooth width, E₁ and E₂ are the elastic moduli of the two gears, and v₁ and v₂ are Poisson's ratios of the two gears.

2.3 Gear transmission error

It is assumed that the tooth surface error is small enough relative to the macroscopic structure of the gear, the actual contact point coincides with the position of the theoretical contact point, and the normal direction of each point after the contact does not change, regardless of the frictional force and the lubricating oil effect when the tooth is engaged. Under the action of the meshing force P, if the transmission error generated by the gear pair is δ, there is a load balance relationship:

$$\begin{array}{}\text{(15)}& P=k_{\mathrm{s}}\sum _{i=\mathrm{1}}^n{u}_i=k_{\mathrm{s}}\sum _{i=\mathrm{1}}^n(\mathit{\delta }-{\mathit{\epsilon }}_i),\end{array}$$

where k_s is the stiffness of each contact point, and SMITH considers the stiffness of each slice to be the same, which is derived from the single tooth stiffness formula in ISO6336. Additionally, ε_i is the initial gap amount at contact point i, and u_i is the deformation of each contact point. When δ<ε_i, it indicates that the point has been touched, so u_i takes a positive value, and when δ>ε_i, it indicates that the point is not in contact, so u_i is set equal to zero.

SMITH uses an iterative method to calculate the transfer error. The iterative steps are described in (Han, 2003).

2.4 Backlash function

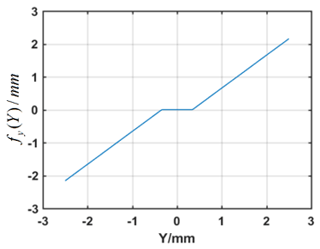
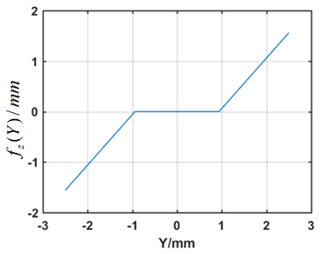
Due to the existence of gear transmission error and the influences of wear and lubrication in the meshing process, the tooth clearance between meshed gears and backlash function can be expressed by a piecewise function. Assuming the tooth gap is Y, the nonlinear backlash function is (Wang and Kang, 2015):

$$\begin{array}{}\text{(16)}& f\left(Y\right)=\left\{\begin{array}{cc}Y-\mathrm{1},& Y>\mathrm{1}\\ \mathrm{0},& \mathrm{|}Y\mathrm{|}\le \mathrm{1}\\ Y+\mathrm{1},& Y<\mathrm{1}\end{array}\right.,\end{array}$$

The corresponding lateral and axial backlash functions can be expressed as:

$$\begin{array}{}\text{(17)}& f\left(Y\right)=\left\{\begin{array}{cc}Y-\sin \mathit{\beta },& Y>\sin \mathit{\beta }\\ \mathrm{0},& \mathrm{|}Y\mathrm{|}\le \sin \mathit{\beta }\\ Y+\sin \mathit{\beta },& Y<\sin \mathit{\beta }\end{array}\right.,\end{array}$$

$$\begin{array}{}\text{(18)}& f\left(Y\right)=\left\{\begin{array}{cc}Y-\cos \mathit{\beta },& Y>\cos \mathit{\beta }\\ \mathrm{0},& \mathrm{|}Y\mathrm{|}\le \cos \mathit{\beta }\\ Y+\cos \mathit{\beta },& Y<\cos \mathit{\beta }\end{array}\right.,\end{array}$$

The lateral and axial backlash functions are shown in Figs. 3 and 4.

Figure 3 Lateral backlash function.

Figure 4 Axial backlash function.

2.5 Mesh damping

The meshing damping is mainly related to the gear meshing damping ratio, average meshing stiffness, and gear quality, and it can be calculated by Eq. (19) (Zhu, 2004):

$$\begin{array}{}\text{(19)}& c_{\mathrm{m}}=\mathrm{2}\mathit{\epsilon }\sqrt{{\displaystyle \frac{K_{\mathrm{s}}{r}_{\mathrm{1}}{r}_{\mathrm{2}}{I}_{\mathrm{1}}{I}_{\mathrm{2}}}{r_{\mathrm{1}}^{\mathrm{2}}{I}_{\mathrm{1}}+r_{\mathrm{2}}^{\mathrm{2}}{I}_{\mathrm{2}}}}},\end{array}$$

where ε is the gear pair relative meshing damping coefficient, K_s is the average meshing stiffness, I₁ and I₂ are moments of inertia, and r₁ and r₂ are base circle radii.

2.6 Wear fault parameters

Uniform wear of the tooth surface changes the tooth thickness as well as the parameters A_i and I_i of the micro-element, which reduces the meshing rigidity. The wear depth corresponding to micro-element i is h_i, and the cross-sectional area (A_i^′) and the cross-sectional area moment (I_i^′) of the micro-element after the tooth surface is uniformly worn are

$$\begin{array}{}\text{(20)}& {\displaystyle }& {\displaystyle }{A}_i{}^{\prime }=A_i-B{h}_i,\text{(21)}& {\displaystyle }& {\displaystyle }{I}_i{}^{\prime }=I_i-(y_i-h_i{)}^{\mathrm{2}}{h}_{i}B.\end{array}$$

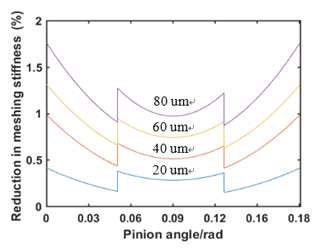
where y_i is the distance from the tooth surface at micro-element i to the neutral layer. Uniform wear of the flank results in a decrease in k_bj, thereby reducing the meshing stiffness of the gear. Substituting Eqs. (20) and (21) into Eq. (12), Eqs. (11)–(14) are used to obtain the gear meshing stiffness after the tooth surface is uniformly worn. The effect of wear fault on gear meshing stiffness is shown in Fig. 5.

Figure 5 Effect of uniform wear of tooth surface on meshing stiffness.

Moreover, when gear teeth produce wear fault, the gear clearances will be larger than in a normal gear (Wang et al., 2011), and the backlash function is:

$$\begin{array}{}\text{(22)}& f\left(Y\right)=\left\{\begin{array}{c}Y-(\mathrm{1}+h_i)\\ \mathrm{0}\\ Y+(\mathrm{1}+h_i)\end{array}\right.\begin{array}{}\\ \\ \end{array}\begin{array}{c}Y>(\mathrm{1}+h_i)\\ \mathrm{|}Y\mathrm{|}\le (\mathrm{1}+h_i)\\ Y<-(\mathrm{1}+h_i)\end{array},\end{array}$$

The corresponding lateral and axial backlash functions can be expressed as:

$$\begin{array}{}\text{(23)}& f_y\left(Y\right)=\left\{\begin{array}{c}Y-(\sin \mathit{\beta }+h_i)\\ \mathrm{0}\\ Y+(\sin \mathit{\beta }+h_i)\end{array}\right.\begin{array}{}\\ \\ \end{array}\begin{array}{c}Y>(\sin \mathit{\beta }+h_i)\\ \mathrm{|}Y\mathrm{|}\le (\sin \mathit{\beta }+h_i)\\ Y<-(\sin \mathit{\beta }+h_i)\end{array},\end{array}$$

$$\begin{array}{}\text{(24)}& f_z\left(Y\right)=\left\{\begin{array}{c}Y-(\cos \mathit{\beta }+h_i)\\ \mathrm{0}\\ Y+(\cos \mathit{\beta }+h_i)\end{array}\right.\begin{array}{}\\ \\ \end{array}\begin{array}{c}Y>(\cos \mathit{\beta }+h_i)\\ \mathrm{|}Y\mathrm{|}\le (\cos \mathit{\beta }+h_i)\\ Y<-(\cos \mathit{\beta }+h_i)\end{array},\end{array}$$

3 Influence of Wear Failure on Nonlinear Dynamics of Gear System

3.1 Nonlinear Dynamic Characteristics of Gear System under Normal Conditions

Figure 6 Bifurcation diagram normal conditions.

Figure 7 System response of w_k=45 Hertz.

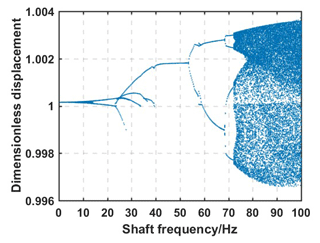
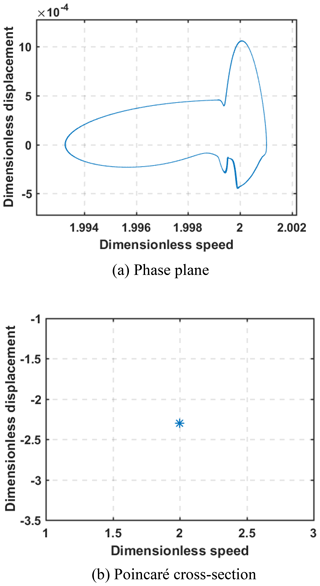
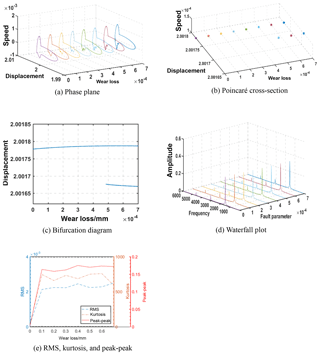
Figure 6 shows the bifurcation diagram of the gear system with the change of shaft frequency (w_k) when the gear system did not fail, that is, the fault value was m=0. As can be seen from Fig. 6, with the increase of w_k, the gear system underwent five stages of change: single-period motion → double-period motion → single-period motion → double-period motion → chaos motion. When 40 Hertz $<w_{\mathrm{k}}<$ 55 Hertz, the gear system exhibited single period motion, and when w_k>72 Hertz, the gear system exhibited chaos motion. Figures 7 and 8 display the phase plane and Poincaré cross-sections of the gear system, respectively. When the shaft frequency was w_k=45 Hertz, the phase plane of the system was one closed curve, and the Poincaré cross-section was one point, indicating that their motion was single-periodic; when w_k=75 Hertz, the phase plane of the system was composed of many closed curves, and the Poincaré section contained many discrete points, indicating that its motion was chaotic.

Figure 8 System response of w_k=75 Hertz.

Figure 9 System response changing with wear loss at w_k=43 Hertz.

3.2 Influence of Wear Fault on Nonlinear Dynamics of Gears

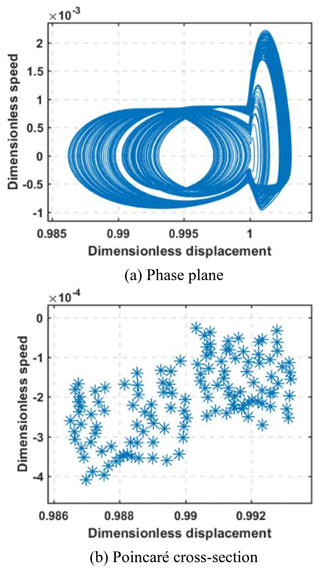
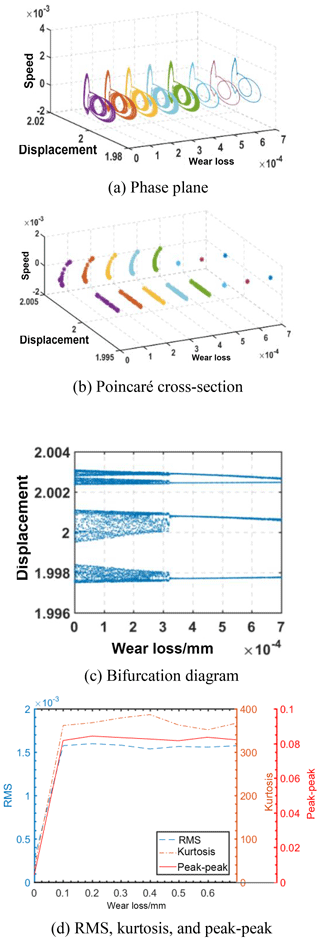
When w_k=43 Hertz, the phase plane, Poincaré section, bifurcation diagram, and waterfall plot of the helical gear system changing with the amount of wear of gear are shown in Fig. 9. It can be seen that phase diagram changed from one closed curve to two closed curves with increasing wear (h); the Poincaré section changed from one point to two discrete points; the bifurcation diagram gradually changed from single-period motion to double-period motion; the spectrum diagram did not change significantly, which shows that gear system changed from single-cycle motion to double-cycle motion with the increase of fault parameters. Figure 9e shows the RMS, kurtosis, and peak-to-peak changes of the acceleration spectrum. During the initial stage of fault, the wear fault had a great influence on the RMS, kurtosis, and peak-to-peak values, which all increased rapidly, but the RMS, kurtosis, and peak-to-peak values all showed fluctuations in state afterwards, indicating that the impact was slight.

Figure 10 System response changing with wear loss at w_k=72.5 Hertz.

Figure 11 Spectrogram.

When w_k=72.5 Hertz, the changes in the phase diagram, Poincaré section diagram, and bifurcation diagram of the helical gear system in response to the increase of wear are shown in Fig. 10. The phase plane changed from many closed curves to two closed curves with the increase of fault parameters; the Poincaré section changed from many discrete points to two points; and the bifurcation diagram gradually changed from a chaotic state to four-fold periodic motion. In summary, all tooth wear failure will change the movement of the gear system from chaos to double-cycle motion. Figure 10d shows the RMS, kurtosis, and peak-peak values of the acceleration spectrum. The RMS, kurtosis, and peak-peak values rapidly increased at the initial stage of fault, and then all of them showed a fluctuating state, and the fluctuation amplitude was small.

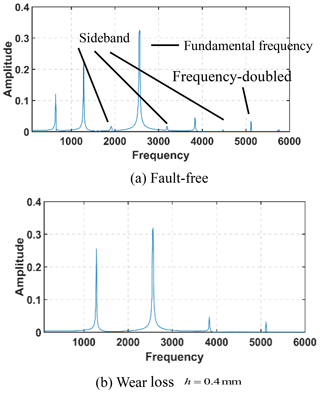
Figure 11a, b shows frequency spectrum for fault-free gear systems, and the amount of wear is h=0.4 mm, from which we can see that wear failure reduced the amplitude of the sideband frequency of fundamental frequency and frequency doubling, and the amplitude of frequency doubling increased when w_k=72.5 Hertz.

4 Experimental verification

Figure 12 is a test bench customized to reduce the center distance of the transmission ratio of a certain high-speed train gearbox. This test bench can effectively simulate the motion of the gearbox under various operating conditions. The input motor can input different speeds, the output motor can apply different sized loads, and the gears interact with one-step meshing. Because no obvious changes can be seen in the simulated spectrogram at low frequencies, this experiment only verifies the effects of wear failure on helical gear systems at high frequencies. The operating conditions were shaft speed n=4380 r min⁻¹ and load torque T=100 N m⁻¹. Gear with wear fault were tested, and normal gear were used as the control. The wearing amount of the wear fault gear was 0.3 mm, and the tilt angle of gears was 26^∘. Figure 13 shows the gears used in the experiment.

Figure 12 Gearbox test bench.

Figure 13 Gears used in experiment.

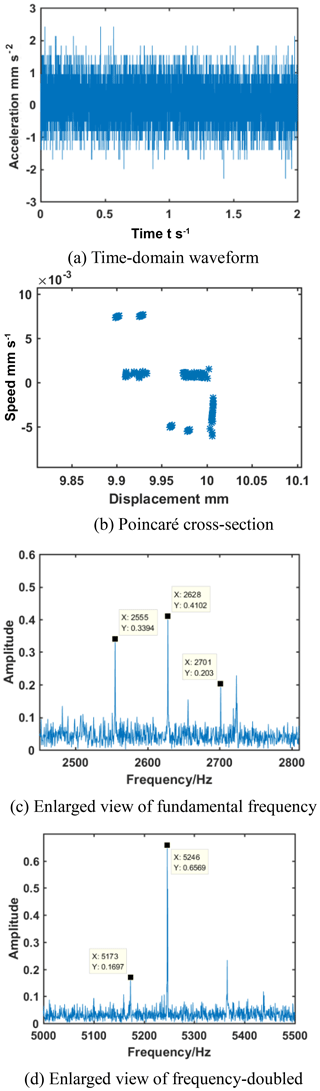
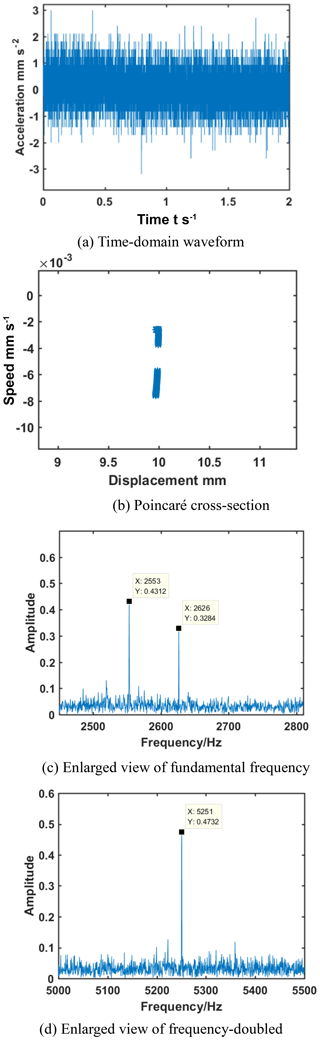
Figures 14 and 15 show the time-domain signal and spectrogram of the normal gear and wear fault gears under the same conditions. The calculated rotation frequency of the driving gear was 73 Hertz, and the rotation frequency of the driven gear was 29.2 Hertz. The meshing frequency was 2628 Hertz. From Fig. 14, when the normal gear was at n=4380 r min⁻¹, the Poincaré cross-section was many scattered points, and motion state was chaotic. In the enlarged view of one time frequency, 2628 Hertz was the fundamental frequency, and 2555 and 2701 Hertz were the shaft frequencies. There were more abundant sidebands around the fundamental frequency. In the enlarged view of frequency-doubled, 5246 Hertz was frequency-doubled, the sidebands were richer, and the amplitude was higher. However, from Fig. 15, the Poincaré cross-section could be approximated as two clustered points, and the motion state was roughly double-period motion. In the enlarged view of fundamental frequency, the sideband frequency was significantly reduced compared to the normal gear, and the amplitude was also significantly reduced. One of the shaft frequency amplitudes increased, and the other decreased. In the enlarged view of frequency-doubled, the amplitude of the sideband was significantly reduced. Although the amplitude of frequency-doubled was not increased as predicted by the simulation, the other results were basically the same as those obtained from the simulation analysis.

Figure 14 Time-domain signal and spectrogram of the normal gear at n=4380 r min⁻¹.

Figure 15 Time-domain signal and spectrogram of tooth surface wear gear at n=4380 r min⁻¹.

5 Conclusions

Qualitative and quantitative methods were used to study the influence of wear fault on the bifurcation and chaos characteristics of a helical gear system. The specific conclusions are as follows:

• a.

  With the increase of shaft frequency, the helical gear system of a high-speed train undergoes five stages of change: single-period motiondouble-period motionsingle-period motiondouble-period motionchaos motion. Wear failure will make the gear system move from single period motion to double period motion at low frequencies. At high frequencies, however, the gear system will gradually evolve from chaotic motion to double-period motion, and the sidebands of fundamental frequency and frequency doubling will decrease. Wear failures have the greatest impact on RMS, kurtosis, and peak-to-peak values at the initial failure stage; then all of them show a fluctuating state, and the fluctuation amplitude is small.

• b.

  The influence of wear failure was verified experimentally by a gear test bench. The spectrum signal obtained at high frequencies was basically consistent with the simulation results.

• c.

  In fault signal diagnosis of high-speed trains, detected signals can be used to identify and diagnose the types of faults and provide guidance for fault diagnosis of high-speed train gearboxes.